三相四线制有源滤波器不同指令电流检测方法的应用研究

连家玉，孙培德

（东华大学 信息科学与技术学院，上海 200000）

1 基于基波正、负序提取的ip-iq法谐波检测法

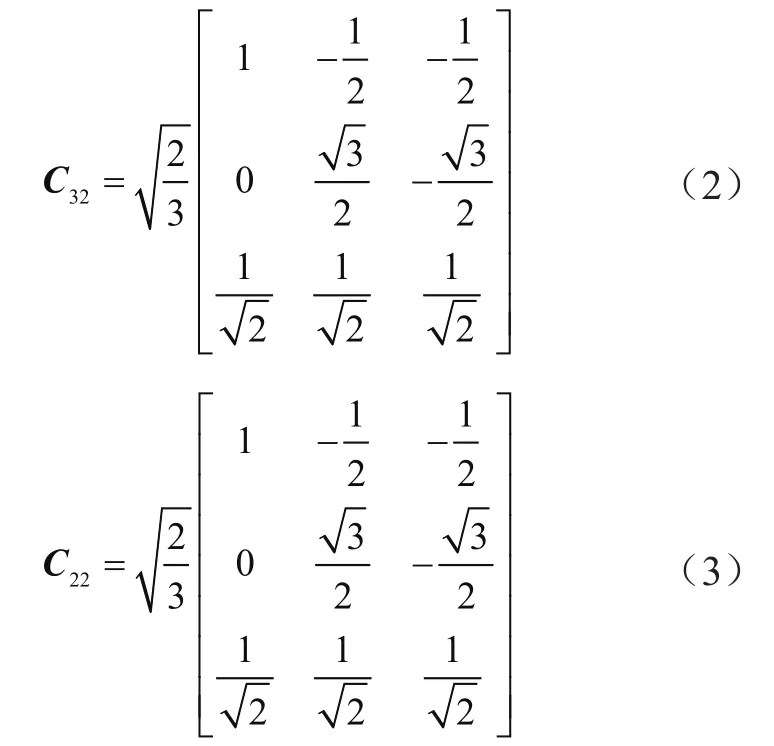
谐波源为三相三线制不对称负载，采用基于瞬时无功功率理论的ip-iq法时，需要使用锁相环和正、余弦信号发生电路得到与a相电网电压Ea同相位的正、余弦弦信号，通过低通滤波器消除模拟滤波器的相位问题，矩阵C32实现iabc到iαβ的变换及其反变换，C22为αβ到dq的变换矩阵。dq坐标系下的ip、iq经过LPF后得到直流分量再通过两次变化得到基波正序分量，最后用负载电流减去基波正序电流，得到负载三相电流中谐波和无功电流[1-3]。

将谐波电流作为检测指令，运用ip-iq法时，还需将负载电流中的基波负序电流提取出来，若将C32和C22的列、行做交换处理，也可提取基波负序分量[4]。但需要再增加4个运算矩阵，电路变得复杂，成本较高。不妨通过公式推导对ip-iq法进行改进，同时计算出基波正、负序电流。负载电流中的每一相都含有正负序电流，电流有效值用I表示，正、负和零序分别用1、2和0表示，n表示谐波次数，φ表示初相角，负载电流ia、ib、ic可表示为：

变换矩阵C32和C22的表达式为：

ia、ib、ic转化成iα、iβ两相静止坐标下的形式为：

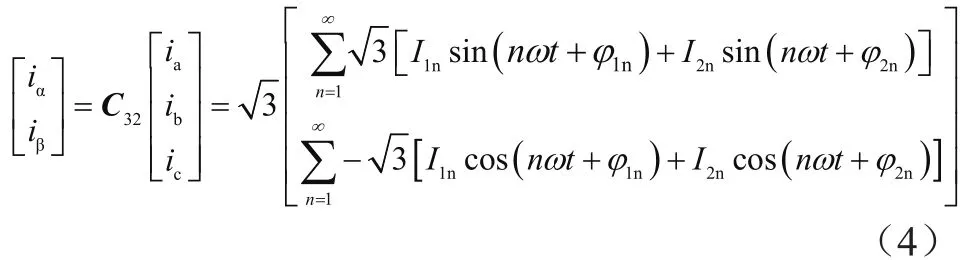
通过计算可得：

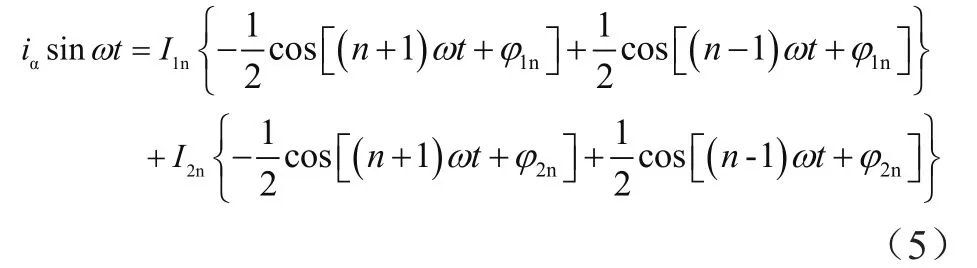
iαsinωt经过LPF滤波后，得到它的直流分量为：

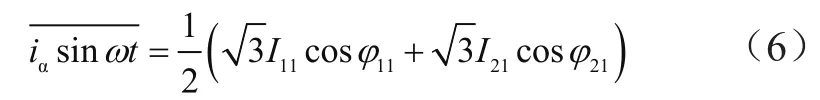
同理-iαcosωt、-iβcosωt以及 -iβsinωt中的直流成分别为：

将-iαsinωt、-iαcosωt、-iβcosωt、-iβsinωt都乘2，得到的量分别设为i′p1、i′q1、i′p2、i′q2，令C1=[sinωt-cosωt]，C2=[-cosωt-sinωt]可得：

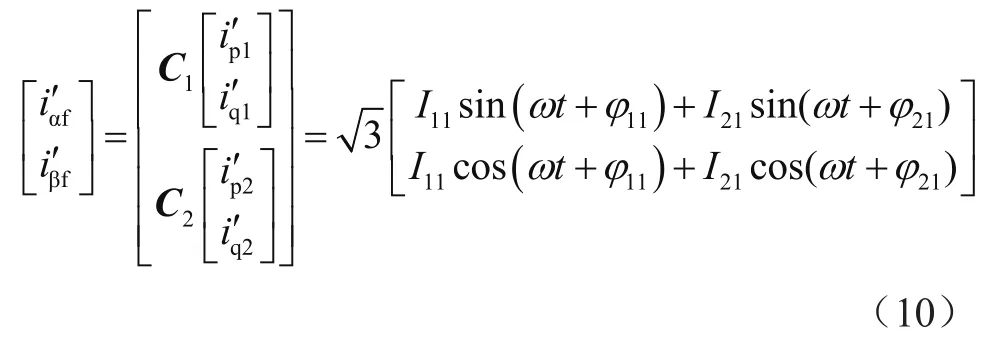
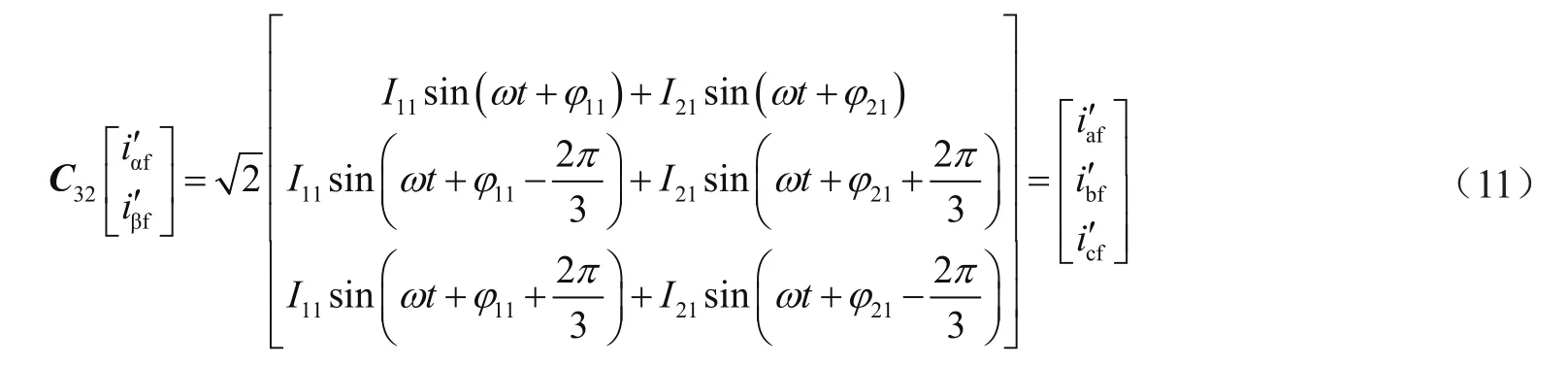
由式（11）可得出三线制负载电流中基波正序、负序电流之和，再用负载电流减去基波正、负序电流便可得到谐波电流。应用到三相四线制负载中时，需要将每相中的零序电流剔除后作为新的三相负载电流，此时新的三相负载电流中没有了零序电流，这里还需要构建一个零序基波的提取模块，将每相零序中的基波成分提取出，用原负载电流减去基波正、负序电流和基波零序电流，就可以得到三相四线制负载的正、负序、零序电流值和[5,6]。三相四线制基于基波正、负序提取的ip-iq法原理如图1所示。

2 基于FBD与ip-iq复合的谐波及无功电流检测法

常用的电流谐波检测算法都存在着各自的优缺点，为了结合ip-iq法的灵活性和FBD法的实时性，通过对两种算法的理论推导，找出其内在联系，将两种算法相结合，取长补短，设三相参考电压为：

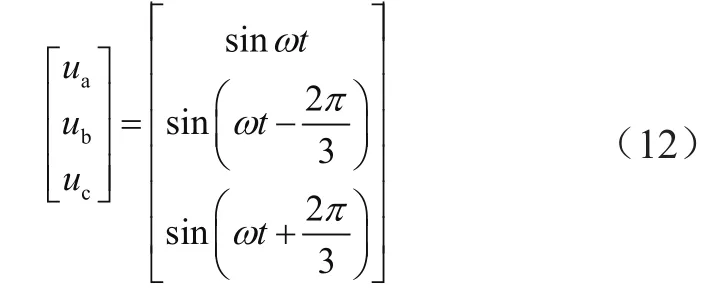
三相四线制负载电流可表示为：

2.1 三相四线制ip-iq法

针对三相四线制负载，运用ip-iq法计算公式原理同三线制负载的运用原理类似，如下：

2.2 三相四线制FBD法

FBD法的主要思想是用串联在各相的理想电导来等效实际电路中的各相负载，认为电路中的所有功率都消耗在该等效电导上，再利用理想等效电导将电流分解[7-9]。依据FBD法的思想，实际电路可等效成k相系统，不妨设电流矢量为i=(i1,i2,…,in)T，代表电流的瞬时值，电压矢量为u=(u1,u2,…,un)T代表各相电压瞬时值。ip是与系统电流i产生相同瞬时功率的电流量，瞬时功率P(t)、瞬时总电压||u||、等效电导G(t)以及功率ip的相定义为：

当检测指令为谐波及无功电流时，使用FBD法不需要提取出基波负序分量，只需用负载电流减去基波正序电流就可以得到负载电流中的谐波和无功成分，不需要运算基波负序电流，也降低了计算复杂度。基波正序有功、无功电导的表达式为：

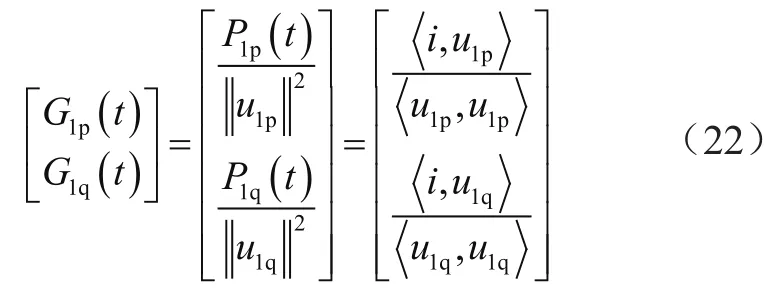
代入三相负载电流和参考电压后，得到：

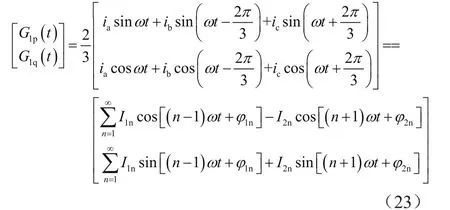
有功、无功电导经过LPF后，得直流分量分别为：

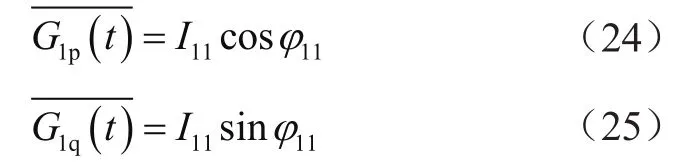
将上面的两个直流分量乘相应的参考电压就可获得基波正序有功、无功电流，将他们相加就是基波正序电流：

再用负载电流减去基波正序电流，就可得到所需的谐波及无功电流。FBD算法运用到三相四线制APF中，通常先将三相电流中的零序电流剔除，但这会增加算法的复杂性和不稳定性。由文献[10]推导证明，即使不剔除零序电流，经过FBD法得到的有功、无功电导中已不含有零序电流，本文也已仿真验证该推导，所以为了减少算法的计算量，可以不用处理三相负载上的零序电流。

2.3 三相四线制FBD和ip-iq结合检测法

通过对比式（16）和式（23）可以发现，ip-iq法中的有功和无功分量ip、iq分别是FBD法中有功、无功电导的倍，所以可以得到：

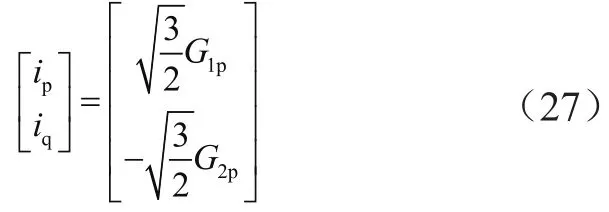
因此算法的前半部分可采用FBD法，后半部分使用ip-iq法，经LPF提取到直流分量，用ip、iq减去它们的直流参考分量得到交流分量，经过前半部分FBD法的处理，ip、iq中已经不含零序电流，此时的谐波（正、负序）和基波负序有关，这里还缺少零序的基波和零序的谐波，即零序电流，所以在矩阵的反变化之前要加入一个补偿零轴的电流i0，然后3个量经过两次反变化后，就可得谐波及无功电流。

三相负载电流无需剔除零序的FBD与ip-iq结合检测法原理框图如图2所示。

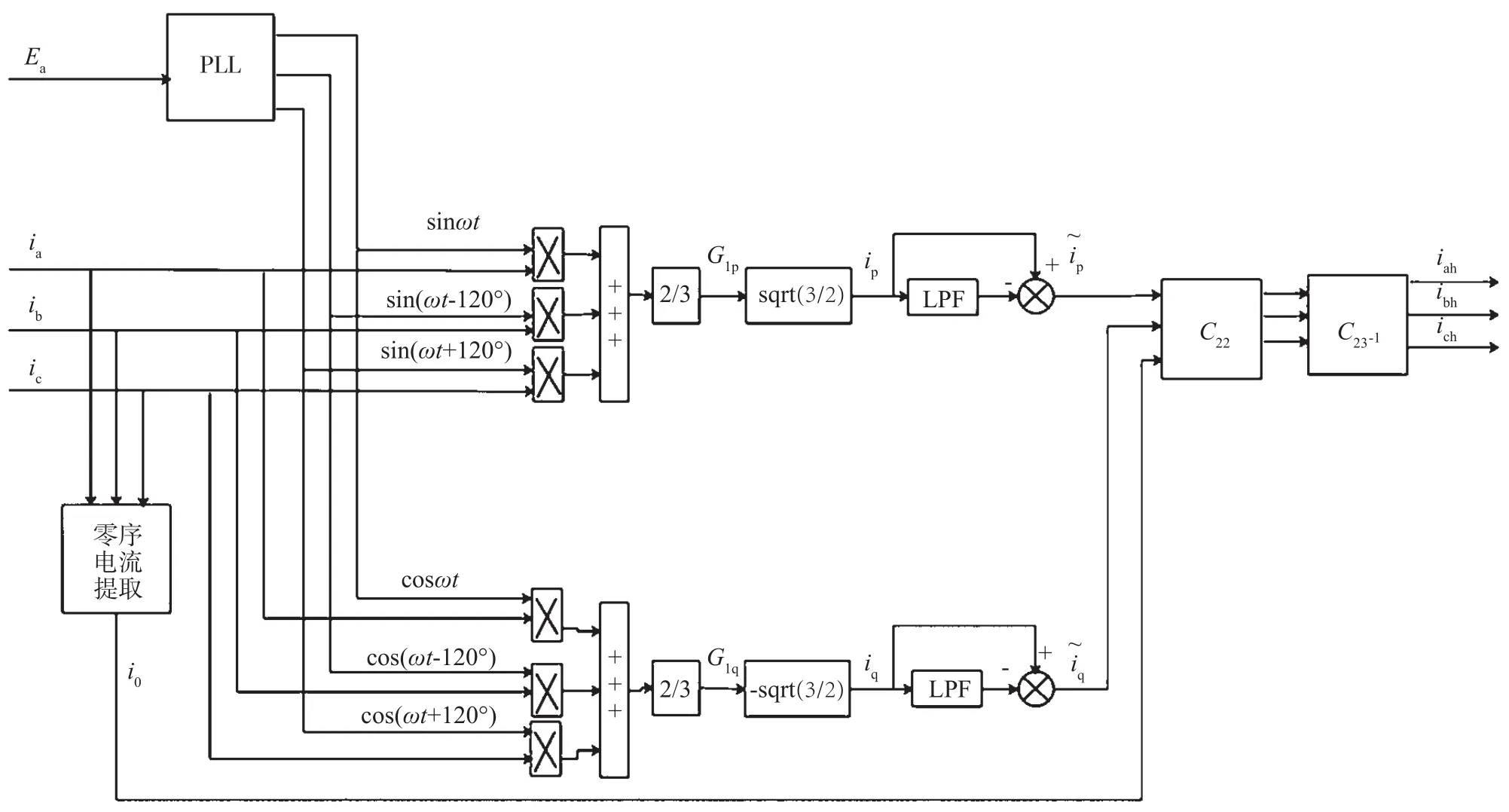
图2 FBD与ip-iq结合检测法原理框图

3 实验结果仿真

通过Simulink仿真软件建立仿真系统对实验结果进行验证，APF主电路结构采用上下电容中分式三桥臂变流器，交流侧电压设置为380 V/50 Hz，采用一个三相不控整流整流桥和一个单相不控整流桥通过a相连接作为谐波源，阻感负载分别为R=30 Ω，L=1 mH。APF主电路的上下电容均为400 V，变流器输出为RL，其中R=0.02 Ω，L=5 mH。为了验证两种不同的检测方法的到的治理效果，采用同样的电流控制器和电压控制器。

负载电流如图3所示，由于b相的谐波含量较多，选用b相负载电流来分析，由图4可知，b相的负载电流THD为27.46%，谐波畸变率较大，主要由基波、5次、7次、11次、13次以及17次等奇次谐波构成。

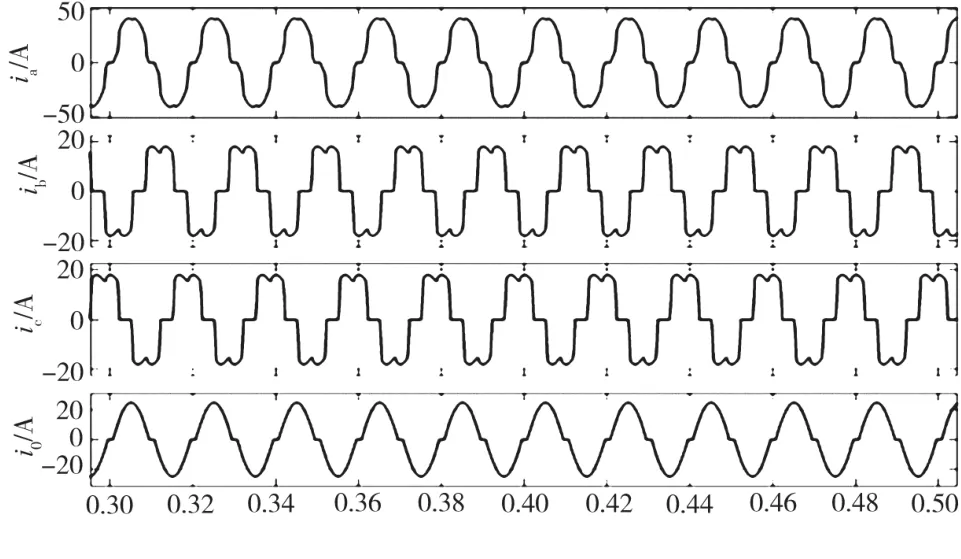
图3 负载abc三相及中线电流

图4 负载b相电流的谐波畸变率

检测电路采用改进的ip-iq法，提取的b相的基波电流和谐波电流如图5所示，检测电路采用FBD与ip-iq结合法，提取的b相基波正序电流和谐波及无功电流如图6所示。

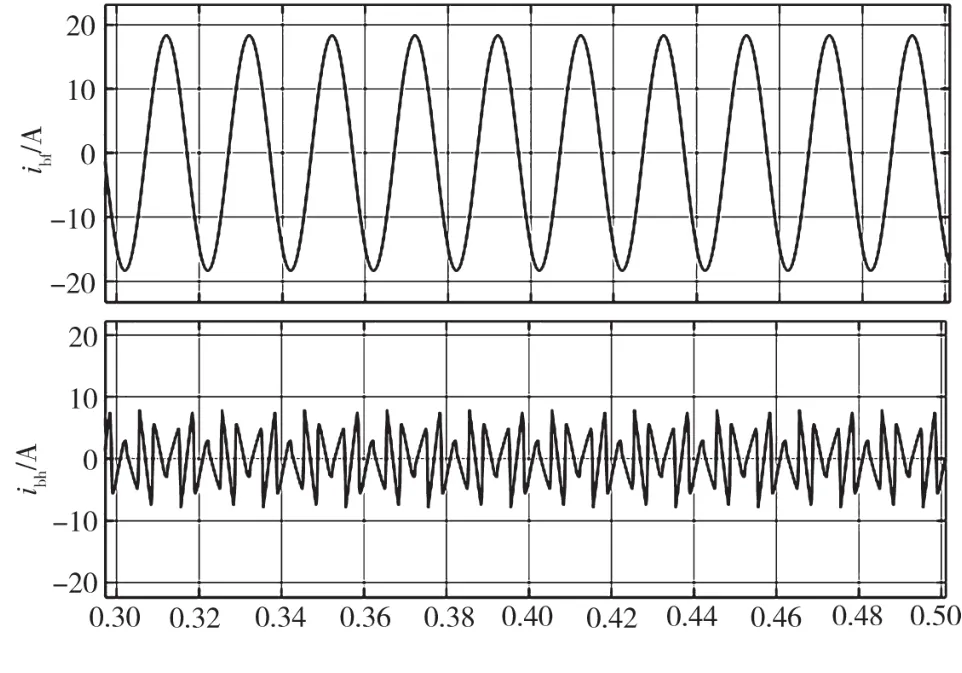
图5 b相基波电流、谐波电流提取

图6 b相基波正序电流、谐波及无功电流提取

选用3D-SVPWM调制方式，配合PID控制器使用，得到两种检测方法的治理效果，指令电流采用改进的ip-iq法和FBD与ip-iq复合法后，网侧三相及中线电流治理效果如图7和图8所示[11-13]。

图7 基于改进的ip-iq法的治理效果

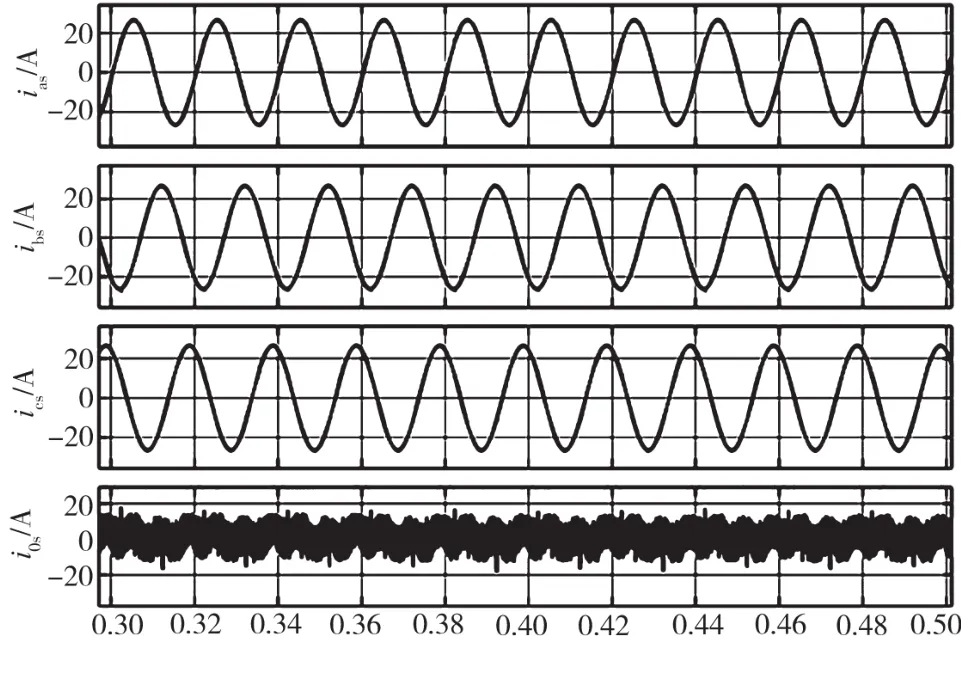
图8 基于FBD与ip-iq复合法的治理效果

两种不同检测方法得到的指令电流，经过电流跟踪补偿电路后，得到的负载三相电流的谐波畸变率均在5%以内，趋于正弦波。验证了改进的ip-iq法、FBD与ip-iq复合法在三相四线制不对称负载系统中应用的可行性。

4 结 论

实际生产生活中，在非正弦周期的三相交流电路中，中性线电流可能远大于相线电流，这就可能造成零线触头的灼烧，易造成安全事故。而基于改进的ip-iq法治理后的中线电流较小且波形趋于正弦，没有远超相线电流值，基于FBD与ip-iq复合检测法治理后的负载中线电流值小于2 A，因此两种指令电流的检测方法都可以在实际工程中应用。