面向输弹一致性的某输弹机稳健优化设计研究

林通， 钱林方， 陈光宋， 刘太素

(南京理工大学 机械工程学院， 江苏 南京 210094)

0 引言

弹药分装式装填在中大口径火炮中有着广泛运用，这种装填方式可使弹药分别由输弹和输药机从炮尾后部快速稳定地输入炮膛。输弹机在输弹过程中，需要保证弹丸达到一稳定卡膛速度，确保卡膛牢靠，同时还要保证卡膛姿态和卡膛位置的一致性。由于弹丸卡膛一致性对弹丸炮口状态有着较大影响[1-3]，为确保弹丸炮口状态参数的一致性，对输弹的卡膛性能有着越来越高的要求。弹丸卡膛起始点运动参数的一致性(输弹一致性)直接影响弹丸卡膛姿态一致性，而输弹机参数决定了输弹过程的初始条件和运动规律。因此研究输弹机参数对输弹一致性的影响，对提高输弹的可靠性以及输弹机设计有重要意义。

在以往对输弹过程研究中，李伟等[4]考虑了液压系统参数随机性并分析了随机参数漂移对供弹与输弹系统动作可靠性的影响。石海军等[5]分析了输弹力、接触碰撞对卡膛速度及卡膛姿态的影响。赵良伟等[6]研究了不同输弹初始速度以及弹丸轴线与身管轴线的高低不重合对弹丸卡膛稳定性的影响。蒋清山等[7]以输弹速度衰减最小为目标，对弹丸初始姿态参数进行了确定性优化。然而由于制造误差和战场环境差异等因素的存在，自动装填系统中不可避免地存在一些随机性问题，如弹丸本身的质量误差和质心偏心以及每次输弹过程输弹机和身管相对位置波动、输弹油缸压力波动等。输弹过程是一个包含随机性参数的动力学问题，上述因素都对卡膛一致性产生了影响。因此考虑参数随机性的输弹稳健优化设计更加符合实际设计需求。

本文建立了考虑参数随机性的输弹过程动力学模型，从理论上分析了典型输弹过程，根据输弹机的工作原理和输弹实验对输弹模型中的参数进行归纳分类，并给出了随机参数分布。通过动力学仿真得到了弹丸卡膛速度一般性规律，在此基础上建立了面向输弹一致性的输弹机稳健优化模型，并对输弹机参数进行了优化计算。

1 输弹运动建模

1.1 基本假设

为了研究输弹过程，基于输弹机工作原理，作出如下假设：

1)弹丸输弹运动可简化成6个自由度的刚体运动，即随质心的3个平动和绕质心的3个转动；

2)输弹过程中输弹机和身管固定不动；

3)弹丸与托弹板、炮尾、身管的碰撞为弹性碰撞；

4)当坡膛结构和弹带特性确定后，弹丸卡膛姿态由弹丸到达卡膛起始点的运动参数确定。

1.2 结构描述

图1(a)所示为输弹机与炮身的相对位置关系。托弹板的前端面紧贴炮尾尾端面。图1中：托弹板直径为Dt、长度为Lt；强制输弹距离为Lt1；第1坡膛起始端距炮尾的距离为Lw；第1坡膛的长度为Lp1；第2坡膛的长度为Lp2；身管尾端起始端的内直径为Dw1；第1坡膛起始端的内直径为Dw2；第2坡膛起始端的内直径为Dp1；身管直膛段的内直径为Dp2；身管尾端面至炮尾尾端面的距离为Lp；炮尾槽上的圆柱直径为Dp；身管仰角为φ0；托板轴线与身管轴线夹角为φΔ. 由于弹丸弹带直径与前定心部直径不相等，弹丸在托弹板上相对于托弹板中心轴线存在一倾斜角，用φzd表示。

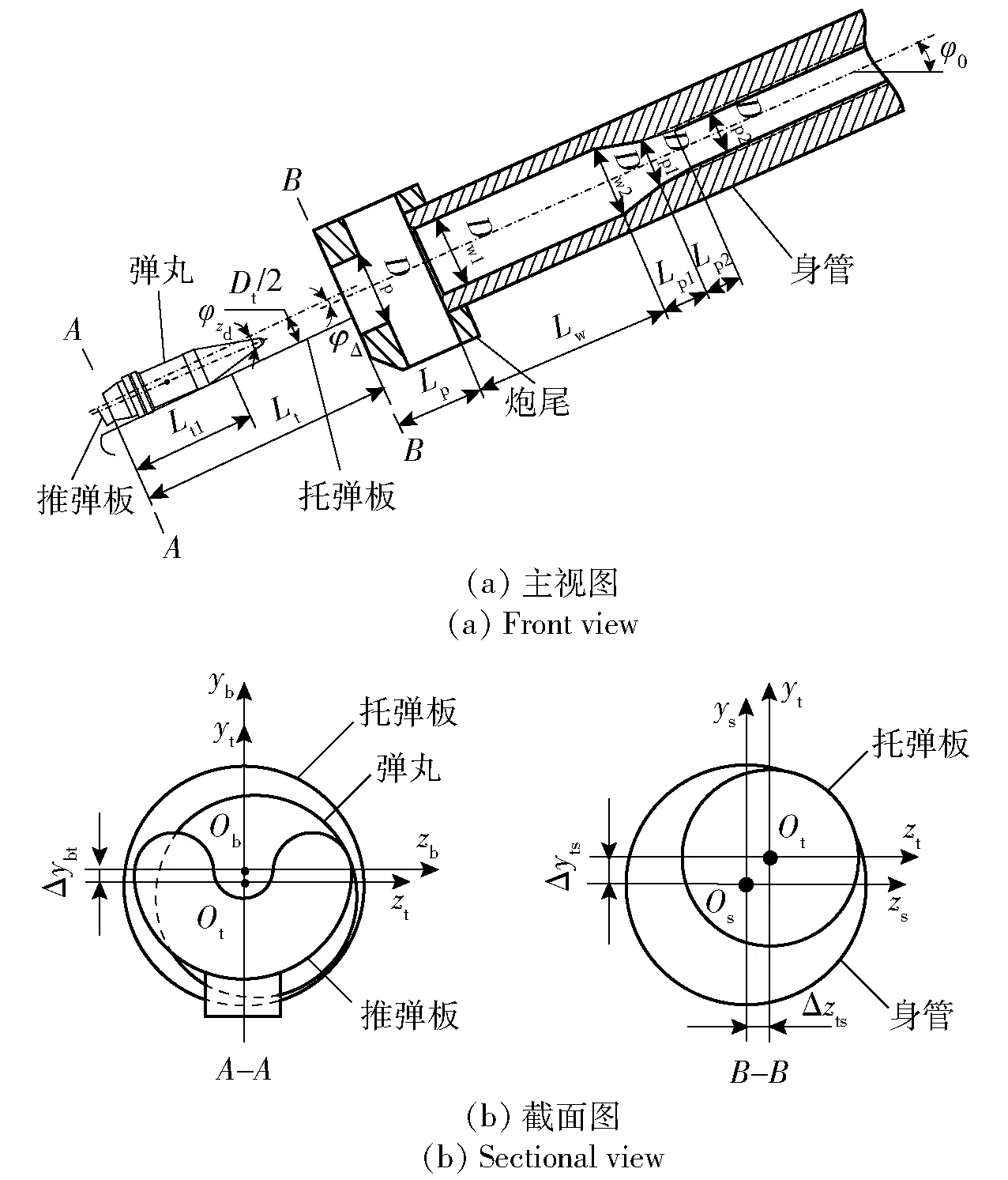
图1 输弹机与炮身相对位置关系Fig.1 Relative position of ramming mechanism and barrel

记推弹板坐标系为Obxbybzb，Ob位于推弹板前端面与其轴线的交点；记托弹板坐标系为Otxtytzt，Ot位于托弹板前端面与其轴线交点。身管坐标系为Osxsyszs，Os位于炮尾尾端面与其轴线交点。xb、xt、xs轴方向均沿其各自轴线指向炮口方向，yb、yt、ys轴垂直向上并与xb、xt、xs轴垂直，zb、zt、zs轴由右手螺旋法则确定。图1(b)所示为A-A和B-B截面图，反映了各部件间的相对位置关系。推弹板相对托弹板的高度用Δybt表示，托弹板轴心和身管轴线水平和垂直偏差分别用Δzts、Δyts表示。

1.3 输弹运动分析

输弹开始前，输弹系统处于静止状态。随后输弹机油缸工作腔压力上升，通过齿轮传动推动推弹板运动，弹丸在与推弹板的接触力Ft作用下开始运动。图2给出了输弹过程中弹丸在托弹板上的受力状态示意图，其中图2(a)为前定心部在托弹板上时弹丸的受力状态。图2中：Nd、Nb分别为托弹板对弹丸弹带和前定心部的法向作用力；μdNd、μbNb分别为对应摩擦力，μd、μb分别为托弹板与弹带、前定心部间的摩擦系数；mg为弹丸重力，m为弹丸质量，g为加速度。随着弹丸逐渐脱离托弹板，Nb、μbNb向弹体转移并越来越小，直至为0，如图2(b)所示。然后弹丸继续运动，整体离开托弹板。

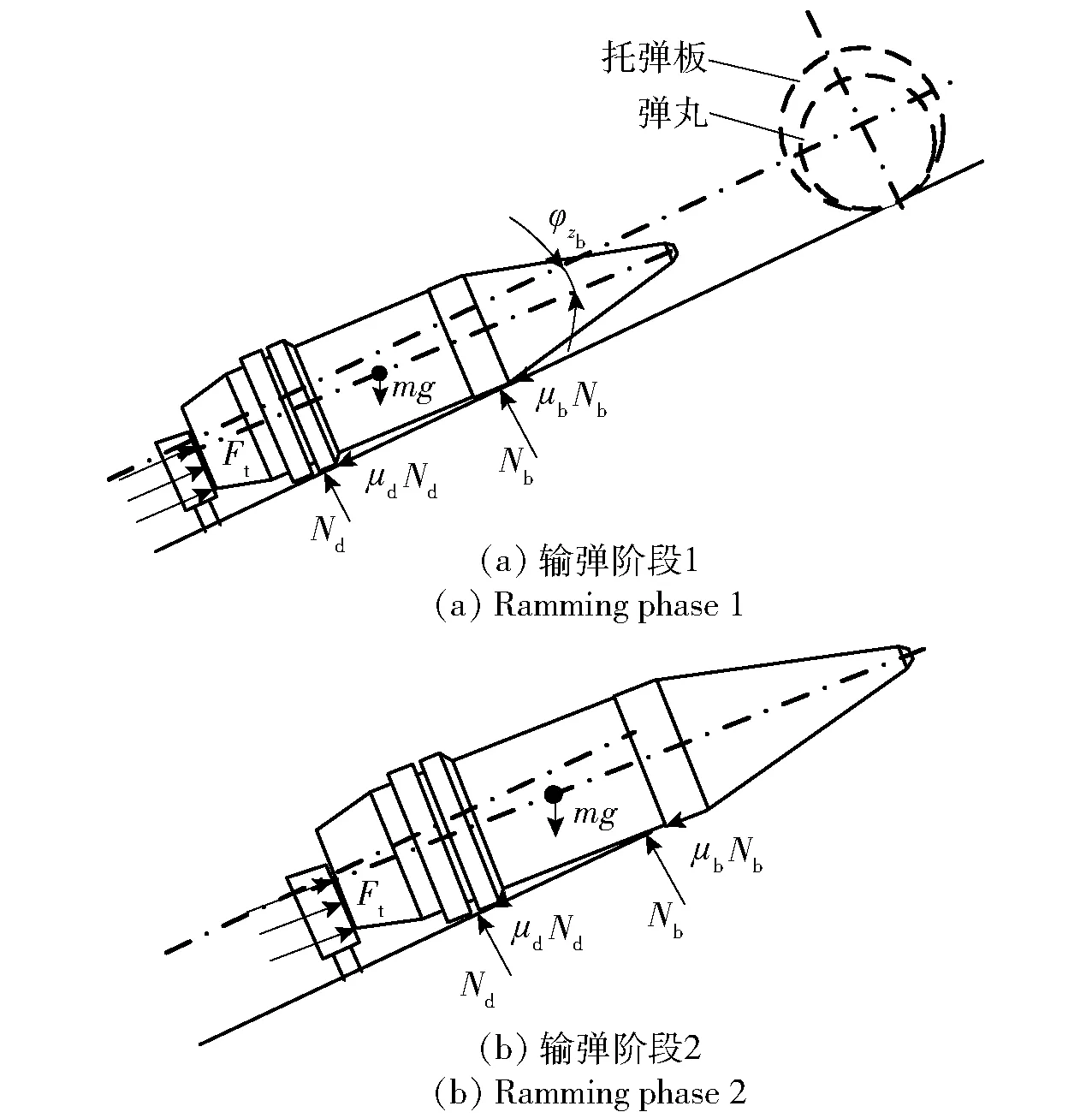
图2 强制输弹过程中弹丸受力Fig.2 Force applied on projectile during ammunition ramming process

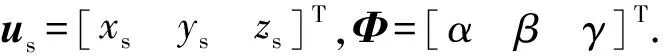
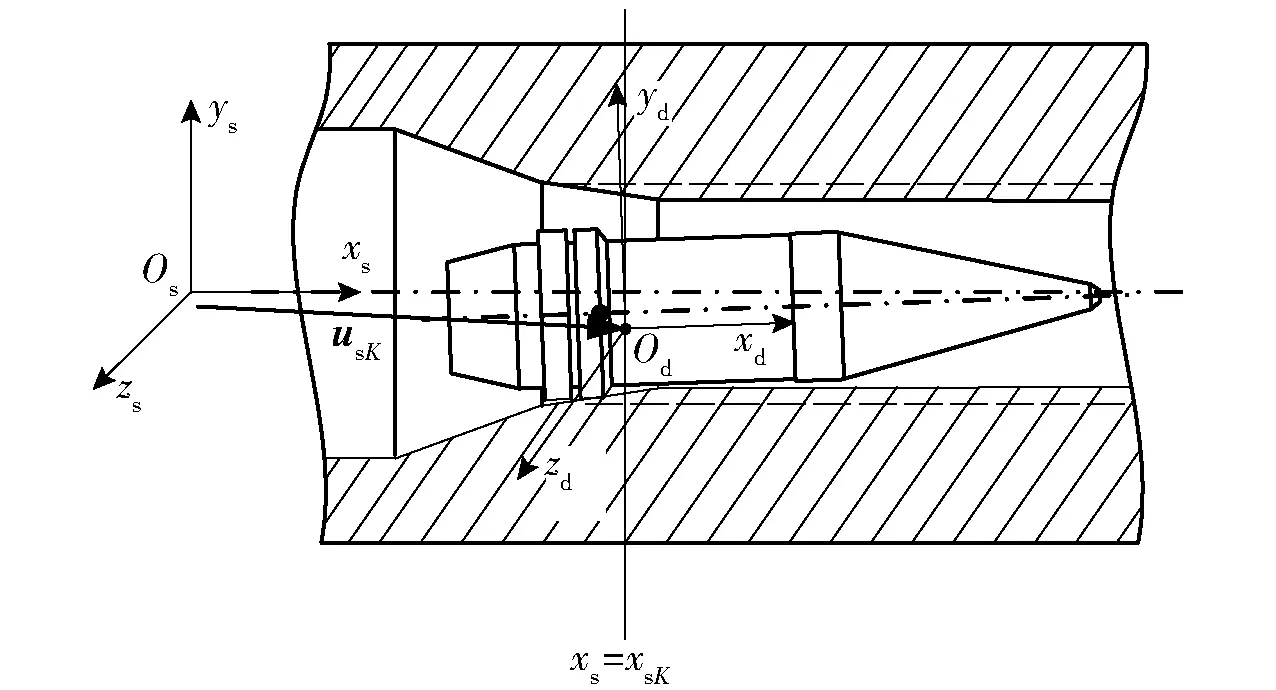
图3 弹丸卡膛时刻运动姿态Fig.3 Projectile movement at bayonet-chamber

1.4 输弹过程动力学建模

基于上述分析，在ADAMS中建立动力学模型，各部件名称如图4(a)所示，输弹模型拓扑结构如图4(b)所示。图4(b)中：h1为身管、炮尾和地面的固连；h2为输弹机与地面固连；h3为齿条、油缸活塞和输弹机间的滑移副；h4、h5为齿轮和输弹机间的旋转副；h6为推弹板和输弹机间的滑移副；h7为输弹机和托弹板的固连；h8为托弹板和弹丸的接触；h9、h10、h11为齿轮、齿条间的齿轮副；h12、h13分别为推弹板、身管与弹丸间的接触。

弹丸与推弹板、托弹板、身管均为实体接触，输弹开始前弹丸为自由状态，弹丸在自身重力作用下在托弹板上达到静平衡，弹底与推弹板接触。随后开始输弹过程仿真，在输弹油缸活塞上施加载荷推动齿条齿轮，最终推动推弹板和弹丸向前运动，当弹丸到达卡膛起始位置时仿真结束。

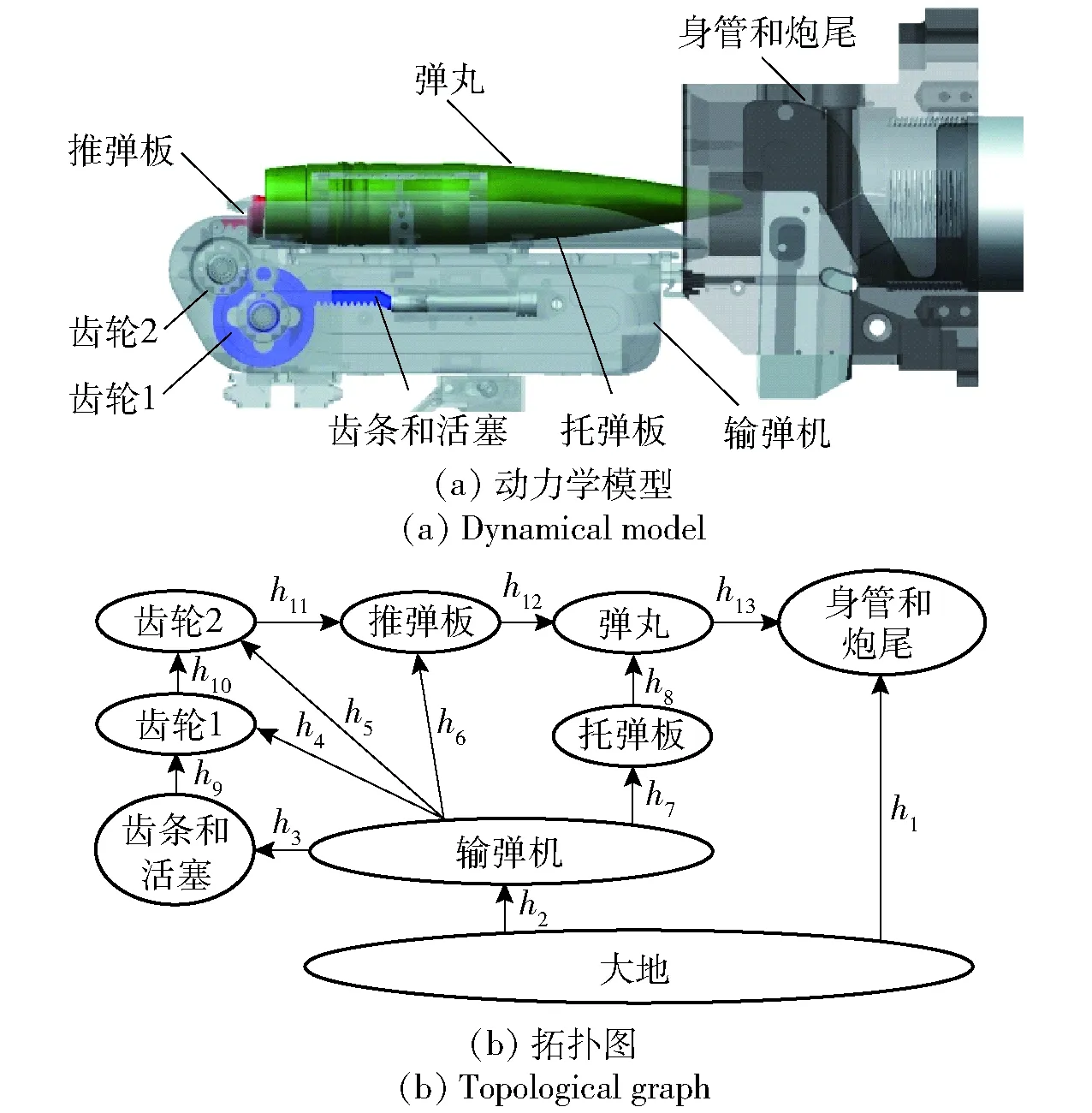
图4 输弹动力学仿真模型Fig.4 Ammunition ramming dynamical model

通过实验得到的输弹机油缸压力实测数值如图5所示，图中给出了51°仰角时3次输弹过程中输弹油缸压力随时间变化的曲线。由于油缸压力变化复杂，为了研究油缸压力并对其建模，将输弹过程油缸压力ps变化简化为0～t1和t1～t2两段，即在t1时达到峰值p1，t2时降到p2，如图6所示。

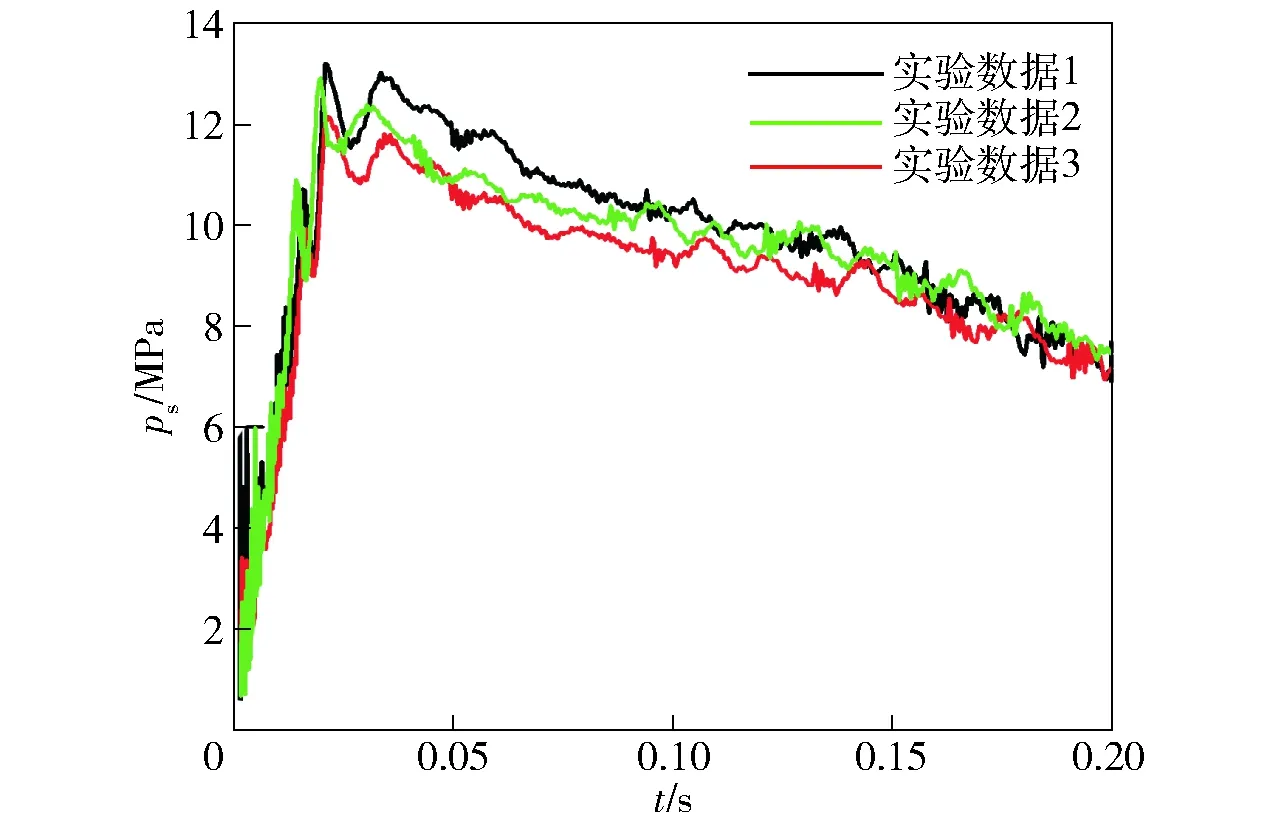
图5 输弹实验油缸压力随时间变化曲线Fig.5 Experimental cylinder pressure vs. time

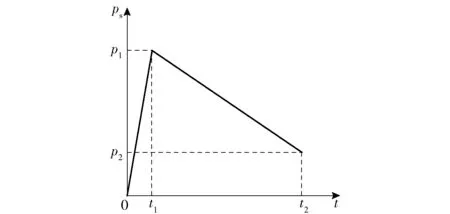
图6 输弹模型油缸压力规律Fig.6 Cylinder pressure vs. time in dynamic model

当弹丸与推弹板、托弹板以及身管内膛发生接触碰撞时，其接触刚度按照Hertz接触定律计算[8]，接触碰撞力等效为弹簧阻尼模型，当穿透量为δ时法向接触力Fn可表示为

(1)

式中：k为接触刚度；n为非线性指数；dmax为阻尼达到最大值cmax时的穿透深度，取值由两碰撞部件的材料而定；step(δ,0,0,dmax,cmax)为阻尼c的计算函数，表示穿透量δ从0变化到dmax时，阻尼c对应的从0变化到cmax. 模型中接触碰撞所需的摩擦力由Coulomb摩擦定律计算。

2 输弹机稳健优化设计

2.1 输弹系统随机参数

弹丸在输送过程中与托弹板的接触、摩擦并与身管内壁发生的碰撞，会造成弹丸速度损失以及弹丸姿态不稳定，从而影响弹丸卡膛一致性。因此，为了提高弹丸卡膛一致性，应通过调整输弹机参数，在保证卡膛速度前提下，使输弹过程更加平稳，保证弹丸卡膛起始点运动参数的波动最小。

输弹模型包含如下参数：

1)输弹机可供调整的结构参数Lt、Dt、Lt1、Δybt；

2)输弹机托弹板与身管的相对位置参数Δyts、Δzts、φΔ；

3)输弹油缸参数t1、t2、p1、p2；

4)炮尾及身管内壁参数Lp、Lw、Lp1、Lp2、Dp、Dw1、Dw2、Dp1、Dp2；

5)摩擦系数μb、μd；

6)弹丸与托弹板轴线夹角φzd.

由于4～6中的参数直接关系到装药结构、药室容积结构以及弹丸结构和材料。在设计时作为给定设计参数而不对其调整。

除输弹机构外，还有弹丸本身的物理属性参数，包括弹丸质量m、弹丸质心距离弹底面距离exd，及其在弹丸坐标系yd轴、zd轴方向的质心偏心eyd、ezd，以及弹丸极转动惯量Ixx、弹丸赤道转动惯量Iyy和弹丸赤道转动惯量Izz，亦不对其调整。

不作调整的参数记为设计参数P，设计参数表示成向量的形式为

P=(Lp,Lw,Lp1,Lp2,Dp,Dw1,Dw2,Dp1,Dp2,
μb,μd,m,exd,eyd,ezd,Ixx,Iyy,Izz,φzd)T.

(2)

将需要优化的参数记为设计变量X，设计变量表示成向量的形式为

X=(t1,t2,p1,p2,Lt,Dt,Lt1,Δybt、Δyts、Δzts,φΔ)T.

(3)

在实际输弹过程中，由于工作环境、控制误差、人工操作等因素，每次输弹过程的初始条件、输入条件存在差异。为了考虑这些随机因素，将设计参数P分为非随机变化的Pd与随机变化的Pp两组数，设计变量X分为非随机变化Xd与随机性的设计变量Xp.

将不作调整的身管尺寸参数，弹丸参数以及摩擦系数归为非随机变化的设计参数Pd，表示成向量的形式为

Pd=(Lp,Lw,Lp1,Lp2,Dp,Dw1,Dw2,Dp1,Dp2,
μb,μd,φzd)T.

(4)

考虑到弹丸加工误差和装药量偏差，每个弹丸的质量、质心位置、转动惯量各有不同，因此在优化模型中将弹丸物理属性参数归为随机变化的设计参数。显然托弹板轴线与身管轴线水平偏差Δzts=0时输弹过程更加平稳，不对其进行优化，仅作为设计参数考虑其随机波动。因此将随机变化的设计参数Pp可表示成向量的形式：

Pp=(m,exd,eyd,ezd,Ixx,Iyy,Izz,Δzts)T.

(5)

非随机变化的设计变量Xd包括需要调整的输弹机结构参数Lt、Dt、Lt1、Δybt表示成向量的形式为

Xd=(Lt,Dt,Lt1,Δybt)T.

(6)

从图5中可以看出油缸压力随机性，即每次输弹油缸压力都会有偏差，在模型中体现为时间t1、t2和输弹油缸压力p1、p2随机性。每次输弹前，由于控制、液压等因素，输弹机翻转到位时，输弹机与身管的相对位置参数存在随机性，Δyts、φΔ为随机变化的设计变量，它们描述了输弹机运动到炮尾时空间运动的精确度。因此随机性设计变量Xp包括油缸压力参数t1、t2、p1、p2和托弹板位置参数Δyts、φΔ，表示成向量的形式为

Xp=(t1,t2,p1,p2,Δyts,φΔ)T.

(7)

2.2 输弹机稳健优化模型

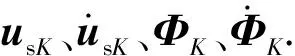
考虑参数随机性的输弹一致性优化问题可以表示为

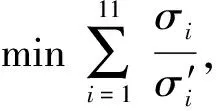
(8)

2.3 优化算法及优化流程

输弹机稳健优化的基本思想如下：在设计变量的设计范围内，根据优化算法选取一组设计变量，依据随机变化的设计参数与设计变量的分布，对随机参数进行采样。然后调用模型，分别代入所采集的样本点数据进行计算，得到这组样本点对应的弹丸卡膛点各运动参数标准差。再根据优化算法选取下一组设计变量，继续计算，直至迭代结束[9-11]。

优化时为了缩减迭代步数、提高优化效率，采用全局优化和梯度优化组合计算策略，以实现优化质量和优化效率的良好折中[12-15]。首先在设定好子种群数、岛屿数、进化代数等参数后，由多岛遗传算法产生初始种群，计算每个个体适应度后，利用竞争、交叉、变异等手段对当前种群进行操作，得到下一代种群，如此反复，直至达到最大代数，获得一组近似最优解。随后运用序列二次规划法，以近似最优解为初值，求解二次规划子问题，以此子问题的解为搜索方向，在局部快速搜索最优解直至收敛。

优化模型将弹丸卡膛起始点运动参数的标准差计入优化目标，因此优化中的每一步都要计算大量样本点来求解其标准差，计算量庞大。为了减少采点数量、提高计算效率，本文采用描述抽样方法，先将随机变量按照等概率进行空间划分，再采用类似拉丁超立方试验设计的思想均匀布点。优化流程如图7所示。

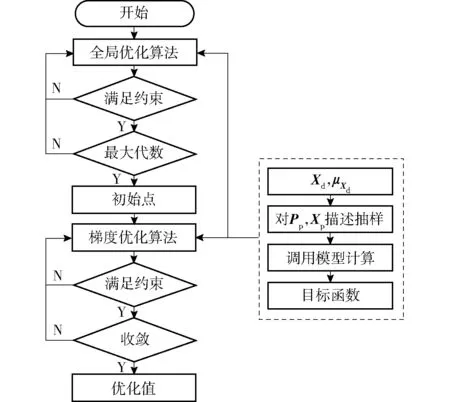
图7 输弹机稳健优化流程图Fig.7 Flowchart of ramming mechanism optimization

3 算例分析

3.1 输弹过程仿真与分析

基于上述分析和假设，在ADAMS中建立某输弹机输弹动力学模型。该输弹机为半强制输弹机，其强制输弹距离为Lt1=600 mm，基本参数如下：

Dt=166 mm，Lt=870 mm，Lw=1 000 mm，Lp=340 mm，Lp1=130 mm，Lp2=156 mm，Dp=170 mm，Dw1=179 mm，Dw2=170 mm，Dp1=157 mm，Dp2=154.94 mm，Δyts=0 mm，Δzts=0 mm，μb=0.15，μd=0.2.

根据大量弹丸测量数据，给出弹丸随机性的结构参数如表1所示。由表1可知，这些参数均服从正态分布。

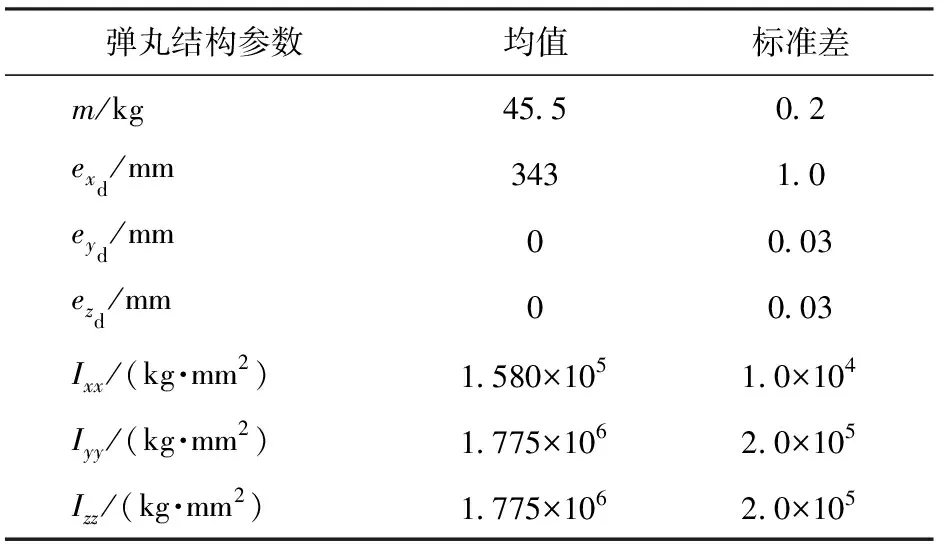
表1 弹丸随机性参数

输弹机在设计时，托弹板轴线与身管轴线重合，因此Δyts、Δzts、φΔ的名义值为0 mm、0 mm、0°. 结合实验工况，给出51°仰角时输弹机随机性设计变量如表2所示。由表2可知，这些参数均服从正态分布。

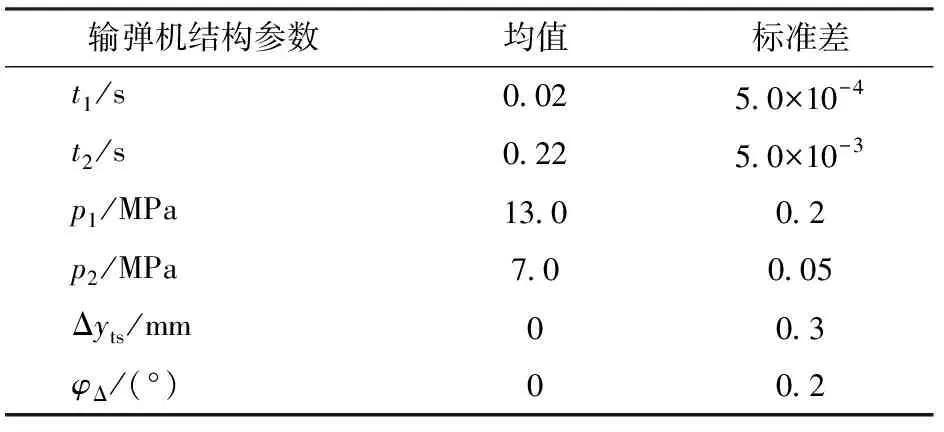
表2 输弹机随机性变量

基于上述随机性参数分布，通过描述抽样500个样本点，得到卡膛速度分布如图8所示。由图8中的数据计算可得，弹丸卡膛速度均值为3 151.14 mm/s，标准差为95.13 mm/s，在显著性水平0.01下通过K-S检验，卡膛速度符合正态分布。从卡膛速度标准差可以直观看出，卡膛速度波动较大，且有可能波动到3 m/s以下，需要对其进行优化。在卡膛速度和随机变化的设计变量均视为正态分布的情况下，(8)式中h取为3.

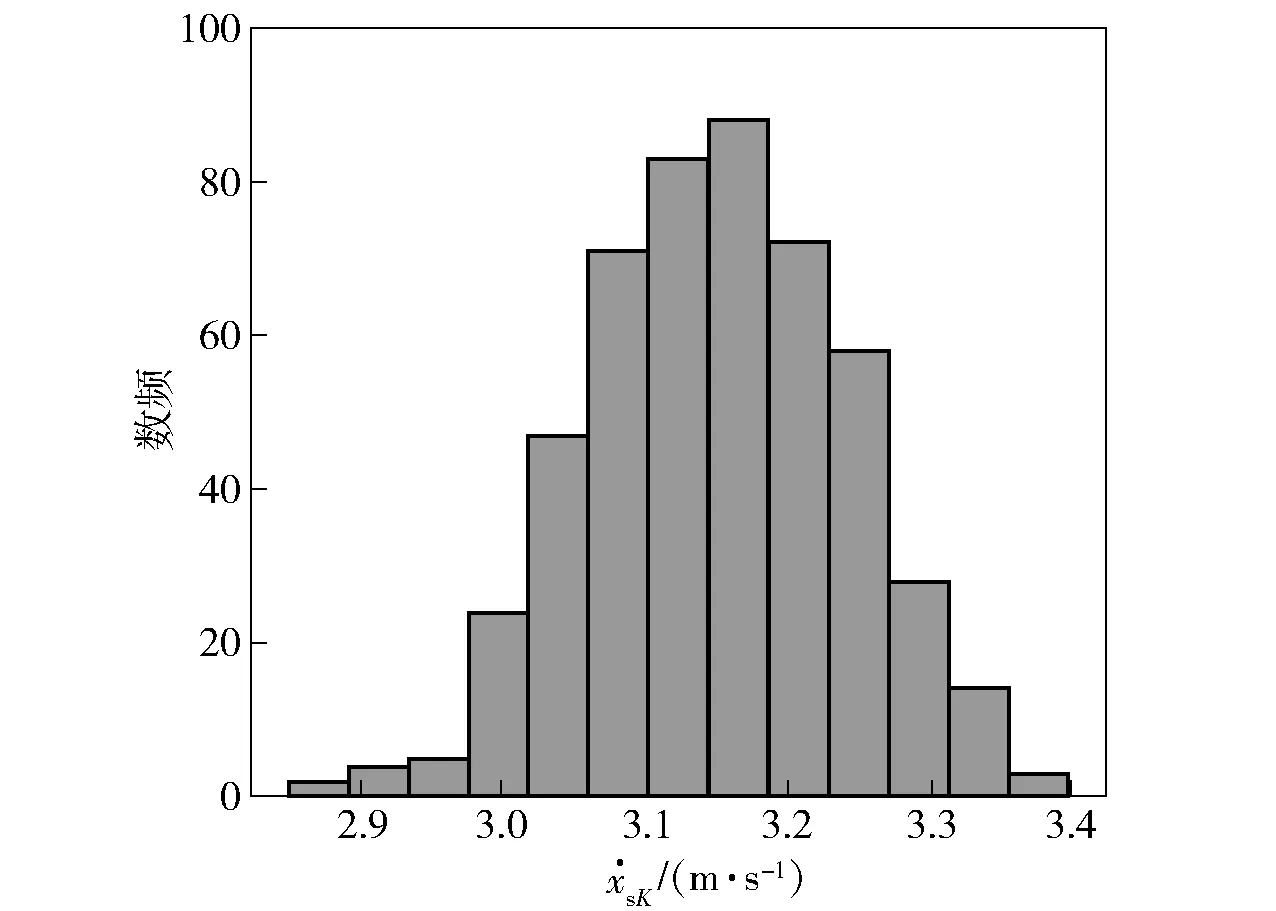
图8 弹丸卡膛速度分布Fig.8 Distribution of bayonet-chamber velocity

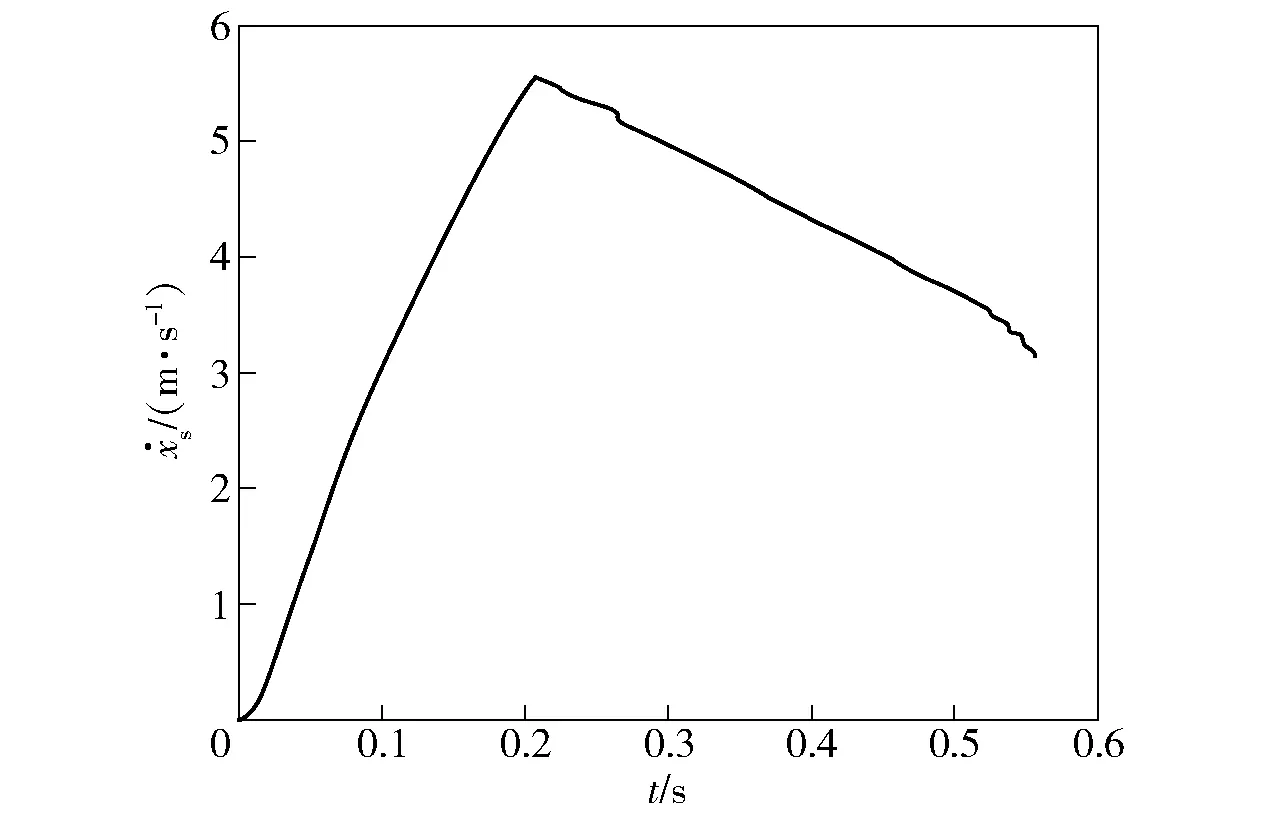
图9 弹丸速度随时间的变化Fig.9 Projectile velocity vs. time

图9和图10分别给出了某样本点对应的弹丸沿身管轴线方向的速度以及欧拉角α、β随时间的变化规律。从图9和图10中可以看出：在强制输弹结束时，弹丸速度达最大值；在随后的惯性输弹阶段，弹丸速度开始下降；由于惯性输弹过程中，弹丸与身管内壁发生碰撞和摩擦，消耗了弹丸动能，速度曲线出现若干折线。当弹丸到达卡膛起始点时，速度达到约3 m/s. 欧拉角中α表征了弹丸高低方向的运动，由图10的欧拉角α曲线可以看出，在弹丸前定心部离开托弹板后，由于重力作用，弹丸有低头的趋势，进入身管后，经过几次碰撞，最终在身管内壁约束下，弹丸轴线趋于身管轴线。β曲线反映出弹丸进入身管后左右摆动，表明弹丸与身管内膛有接触碰撞。

图10 弹丸欧拉角随时间的变化Fig.10 Projectile Euler angle vs. time

3.2 输弹机稳健优化分析

在使用多岛遗传算法优化时，只需要获得近似优化解，涉及计算规模的算法参数取值可适当减小，岛屿数量取5，子群规模数取5，进化代数取5，交叉概率0.8，变异概率0.01，岛间迁移概率0.2，迁移间隔代数2. 使用序列二次规划算法时最大迭代次数取40，收敛精度10-6.

通过稳健优化，得到各设计变量值如表3所示。目标函数在优化迭代中的变化如图11所示。从图11可知，全局优化阶段目标函数收敛较慢，随后梯度优化阶段目标函数逐步减小，收敛较快。优化后结果如表4所示。从表4中可以看出，目标函数降低了21.6%，各个运动参数的一致性得到改善。优化前后卡膛速度概率密度函数如图12所示。卡膛速度分布由N(3 151.1，95.132)优化至N(3 431.1，77.952)，卡膛速度下界满足3 m/s要求，同时卡膛速度的一致性也得到了提高。

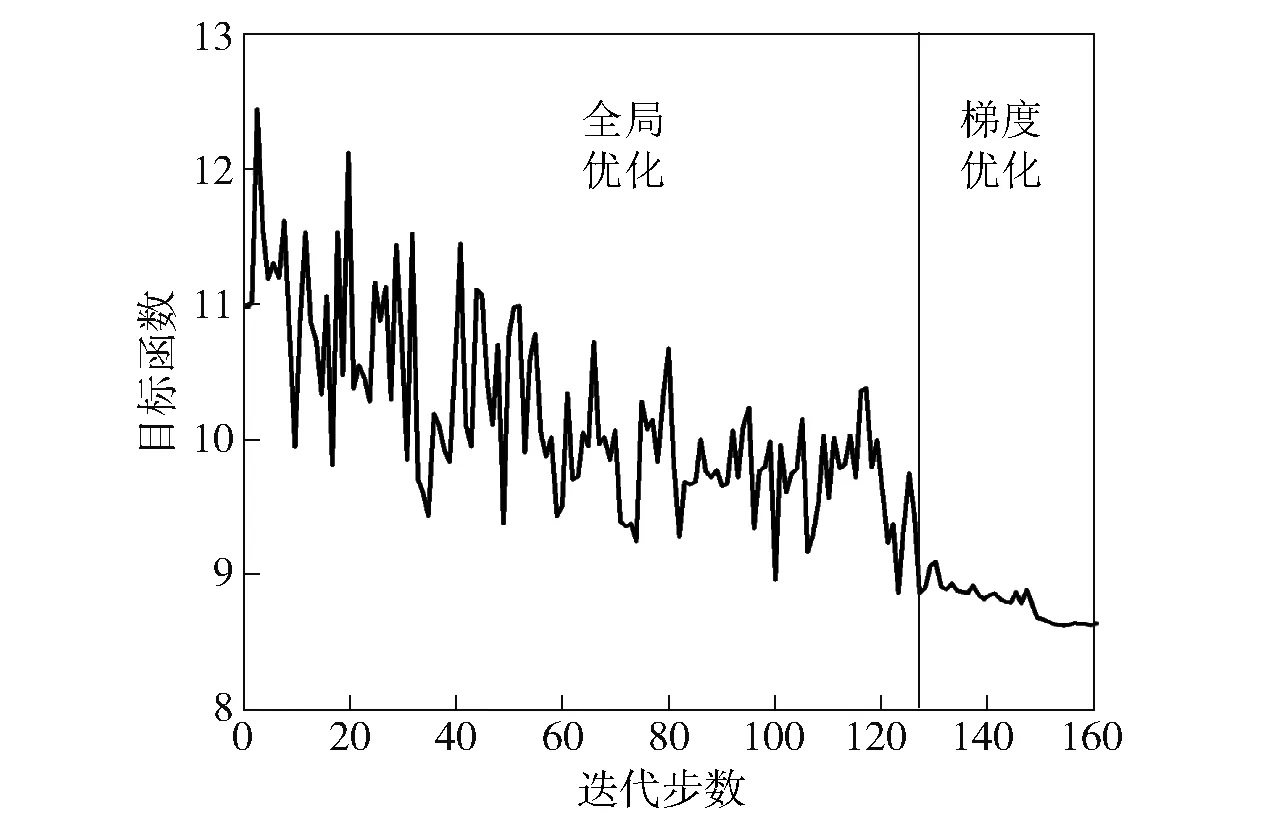
图11 目标函数随优化迭代步数变化Fig.11 Change of objective function in the process of optimization iteration

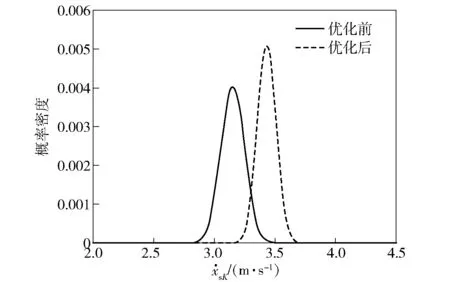
图12 优化前后卡膛速度概率密度函数Fig.12 PDF of bayonet-chamber velocity before and after optimization

表3 优化前后设计变量值

表4 优化前后结果

4 结论

本文阐述了输弹过程的基本原理，对模型中涉及的参数进行了分类，归纳出模型中的设计参数和设计变量，并根据实验给出了随机参数的分布，建立了考虑参数随机性的输弹过程动力学模型。在此基础上建立了针对弹丸输弹一致性问题的输弹机稳健优化模型。优化时运用全局和梯度组合优化算法，采样时运用描述抽样，避免了以标准差为优化目标时的庞大计算量。得到主要结论如下：

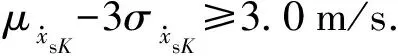
2)在保证卡膛速度达到要求的同时，稳健优化设计通过调整输弹机参数，能有效改善弹丸卡膛起始点运动参数的波动，保证弹丸卡膛一致性。

3)所提优化方法能有效用于输弹系统的优化设计，为输弹机参数的设计提供了一种可靠方法。