舰炮身管的抗振性能优化研究

2019-03-13富威吴琼崔运山刘琪周超

兵工学报 2019年2期

富威，吴琼，崔运山，刘琪，周超

(哈尔滨工程大学机电工程学院，黑龙江哈尔滨 150001)

0 引言

对于舰炮身管自身结构来说，若不考虑其加工制造过程中由于加工条件与环境因素造成的缺陷，结构参数直接决定了舰炮身管的使用性能[1-2]。国内外关于通过结构优化方法提高舰炮身管性能指标的研究方向有所不同，国外偏向于通过改善制造方法和加工工艺来提高舰炮身管的综合使用性能，而国内则偏向于通过优化设计方法，以身管使用性能为优化指标，使得身管复合材料结构达到最优[3]。目前，国内研究内容多偏向于材料结构优化，而忽略了传统的金属舰炮身管。但在实际应用中，舰炮身管材料多为炮钢。因此，金属舰炮身管结构参数优化对于舰炮的实际作战应用更有意义。

1 舰炮身管结构分析的理论基础

1.1 简化模型的确定

舰炮发射过程中，炮尾带动身管一起完成后坐复进运动[4-5]。为了提高舰炮身管振动计算精度，可将身管看作加速移动载荷和弹丸自旋偏心力作用下的3段空心阶梯悬臂梁结构。舰炮身管的实际模型和简化模型如图1所示。

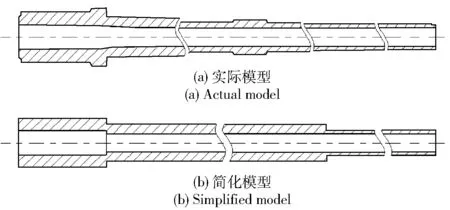
图1 舰炮身管模型Fig.1 Models of naval gun barrel

基于舰炮身管的实际模型，按照图1所示简化结构，得到了舰炮身管各阶的长度、内径和外径简化数值，如表1所示。

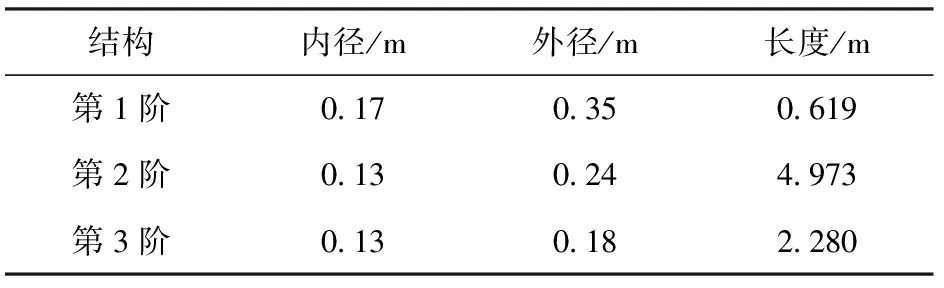
表1 参数简化表

1.2 刚度优化理论的数学基础

通常，研究结构刚度优化问题时，首先需要确定一个衡量刚度指标，一般用结构柔顺度C表示：

C=FTU，

(1)

式中：F为外载荷向量；U为作用力方向的位移向量。结构刚度最大化即为结构柔顺度最小化。C还可表示为

C=UTKU，

式中：K为结构刚度矩阵。

而结构最小应变能矩阵

由此可知E和C之间关系为

在结构载荷与位移等边界条件确定的情况下，以刚度最大为目标函数进行结构优化，其有限元离散形式优化准则可表示为

(2)

式中：C(ρ)为结构单元柔顺度的目标函数；K(ρ)为结构单元的刚度矩阵；H(ρ)为优化模型的约束条件矩阵；M0为结构单元体积系数矩阵；N为结构单元总数量；Ω为结构单元积分区域；ρe为结构材料的密度向量。

引入拉格朗日乘子γ、λ、α≥0、β≥0，进一步分析得到刚度优化目标函数为

(3)

式中：μ1和μ2为引入的松弛变量。

(3)式要取得极值，需满足

(4)

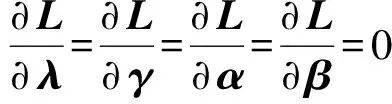
(5)

由(5)式可知：

1)当ρmin<ρe<1，μ1>0，μ2>0时，则有

(6)

2)当ρe=ρmin，μ1=0，μ2>0时，则有

(7)

3)当ρe=1，μ1>0，μ2=0时，则有

(8)

通过上述分析可得结构刚度优化准则为

(9)

式中：Ue为结构节点e的位移向位；Ke为结构节点e的刚度矩阵。

2 舰炮身管结构参数灵敏度分析

2.1 结构参数灵敏度分析

舰炮身管结构参数灵敏度分析有助于确定舰炮身管性能指标对各主要关键参数的敏感程度，即关键结构参数的变化会引起性能指标的浮动量。本文研究的性能指标为刚度和质量，由舰炮身管几何模型中各个设计参数决定，不同参数变化对性能指标影响各不相同[6-10]。

设系统有n个性能指标，且系统性能指标与设计变量之间的表达式为

gj=Gj(vi),i=1,2,3,4,5,6，j=1,2,…,n，

(10)

式中：gj为系统第j个性能指标参数；vi为系统第i个设计变量。gj变化量Δgj与vi变化量Δvi之间关系可表示为

Δgj=(∂Gj/∂vi)Δvi,

(11)

式中：∂Gj/∂vi为性能指标的灵敏度项。

由(2)式得到刚度优化目标函数

C(ρ)=UT(ρ)K(ρ)U(ρ)，

(12)

对(12)式求偏导数，即可得到性能指标的灵敏度公式：

(13)

根据结构单元平衡方程KU-F=0、(12)式与(13)式可得各性能指标灵敏度的等效形式为

(14)

式中：Ee为结构单元应变能。通过(14)式可看出，增加设计变量的数值可以提高结构刚度，且结构刚度是关于结构设计参数标量的单调函数。

根据1.2节舰炮身管简化模型，建立炮口位置刚度数学模型来进行刚度与质量灵敏度分析。模型中，设计变量包括3段身管的长度L1(身管第1间断截面距身管尾端面距离)、L2(身管第2间断截面距身管第1阶段尾距)、L3(身管第3间断截面距身管第2阶段尾距)，内径di1(身管第1段内径)、di2(身管第2段内径)、di3(身管前端面内径)及外径do1(身管第1段外径)、do2(身管第2段外径)、do3(身管前端面外径)。通常，为了满足舰炮弹丸发射条件需要，身管内径是不变的，灵敏度设计变量为长度和外径。

依据刚度定义可将其表示为

[K]{δ}={F}，

(15)

式中：K为刚度；F为外载荷；δ为外载荷作用下产生的位移。当F为单位载荷时，刚度即为单位载荷作用下产生的位移倒数：

(16)

因此，δ通常也被称为结构柔顺度。

根据材料力学中莫尔定理[11]，单位载荷作用下炮口位置产生的位移为

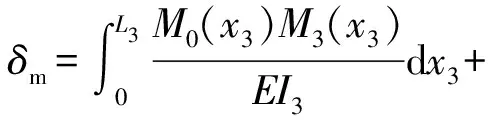
(17)

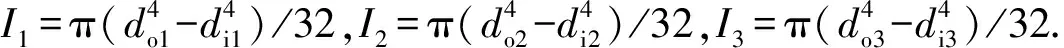
作用载荷为单位载荷，故M0(x)=M1(x)=M2(x)=M3(x)=x，将其代入(17)式，可得各结构参数关于位移的公式。本文采用图形互乘法，得到单位载荷作用下炮口位置产生的位移为

(18)

式中：

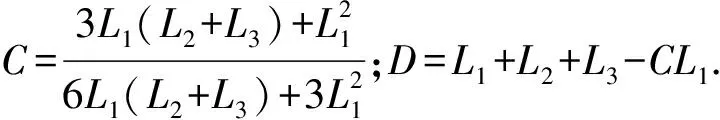
将A、B、C、D代入(18)式，通过MATLAB软件编程计算得到刚度与各关键参数关系为

(19)

(19)式包括模型中的6个关键尺寸参数。为提高舰炮身管结构的多目标优化效率，需确定对性能指标基本没有影响的无关设计变量。如表2所示为根据上述计算过程分析得到的优化变量。

表2 初始设计变量

2.2 舰炮身管性能指标的灵敏度分析结果

根据建立的刚度优化数学模型、灵敏度数学分析方法，以及对舰炮身管刚度公式的推导，通过计算得到刚度性能的灵敏度值。当灵敏度值大于0时，则表示刚度性能与设计变量正相关；当灵敏度值趋于0时，则表示设计参数对刚度性能影响较小，甚至可以忽略[12-13]。如图2所示身管刚度灵敏度分析。

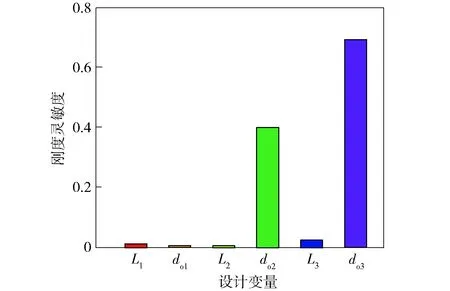
图2 身管刚度灵敏度分析Fig.2 Sensitivity analysis of stiffness

由图2可见，do2和do3灵敏度值均大于0，其他设计参数灵敏度值接近于0，对刚度性能几乎无影响。因此，影响刚度性能指标的参数为do2和do3，在进行刚度优化设计时，二者可作为优化设计变量。

如图3所示，设计变量对身管质量指标灵敏度影响较为明显的为do2、L2、do3、L3，且数值都大于0，表明相互关系为正相关[14]。L1与do1灵敏度值较小，对质量指标灵敏度几乎无影响。因此，影响质量指标灵敏度的参数为do2、L2、do3、L3，在进行刚度优化设计时，可作为优化设计变量。

图3 身管质量灵敏度分析Fig.3 Sensitivity analysis of mass

通过图2和图3进行分析、对比，可确定影响刚度灵敏度与质量灵敏度的参数。进行舰炮身管性能指标多目标优化时，通过灵敏度分析确定的有效设计变量如表3所示。

表3 最终设计变量

3 舰炮身管抗振性能优化

通常，优化算法主要有蚁群算法、遗传算法(GA)。蚁群算法在优化过程中本身很复杂，一般需要较长搜索时间，并且容易出现停滞现象，即搜索进行到一定程度后，所有个体所发现的解完全一致，不能对解空间进一步进行搜索，不利于发现更好的解。而GA可以同时在多点进行信息搜索，具有天生的并行性，并且GA的选择、交叉、变异等运算都是以一定概率进行的，在搜索过程中具有一定灵活性。因此，本文选用GA进行优化。

3.1 GA的优化流程

GA是模拟达尔文生物进化论自然选择和遗传学机理生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。GA具有全局搜索性能强、收敛快等优点，本文用其来解决多目标优化问题。GA流程如图4所示，其中，群体是指舰炮身管1阶固有频率f(X)和质量m(X).

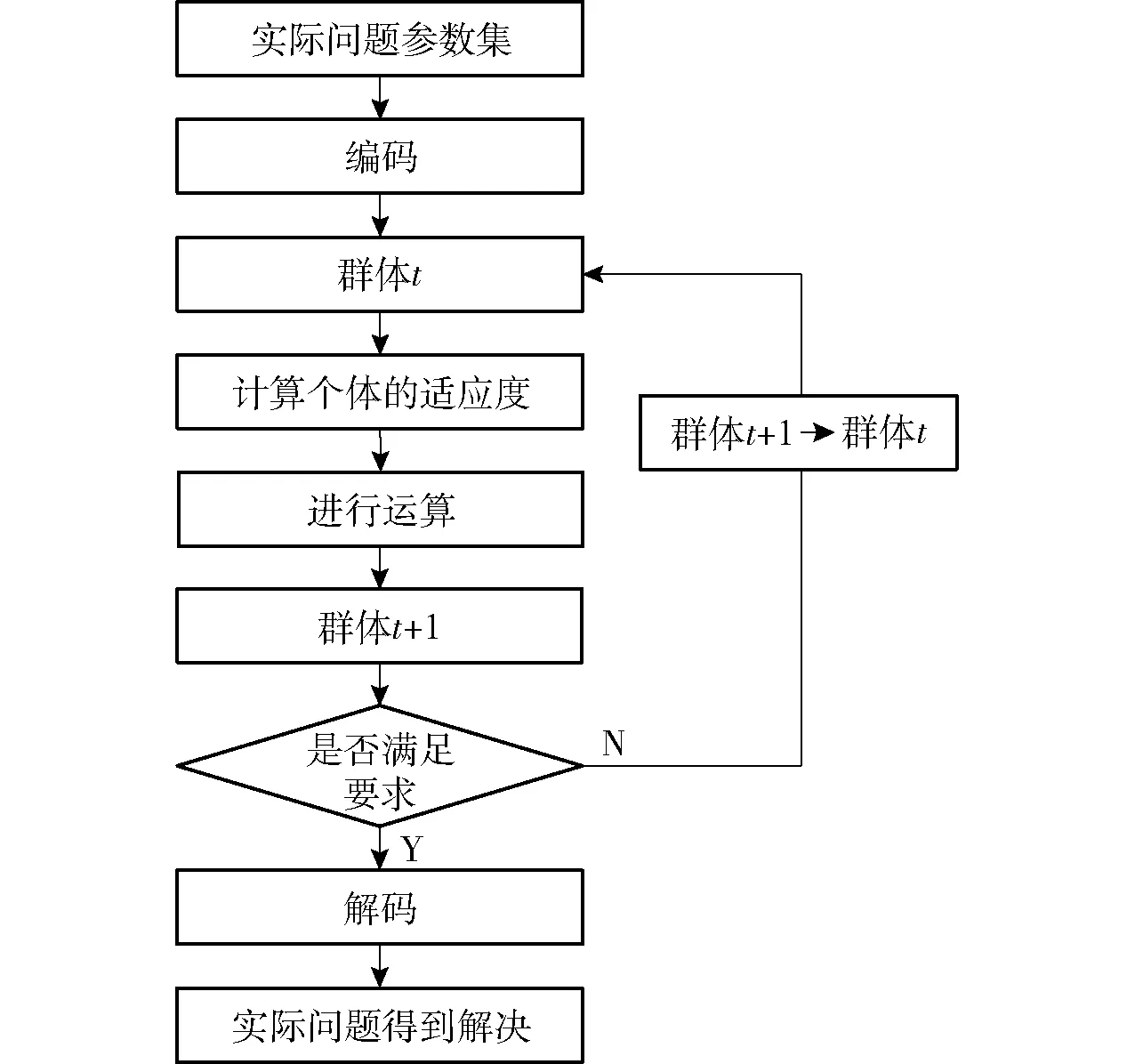
图4 GA设计流程Fig.4 GA design process

本文所涉及的实际问题为对舰炮身管进行抗振性能优化，目的是找出最大f(X)和最小m(X)，从而找出最佳优化参数。

3.2 抗振性能优化过程

大口径舰炮身管抗振性能优化过程如图5所示。

图5 身管抗振性能优化设计流程Fig.5 Optimization design process of anti-vibration performance

1)合理确定舰炮身管的结构设计变量及其取值范围。第2节确定了最终优化参数do2、L2、do3、L3，其尺寸约束分别为

(20)

从(20)式可看出，舰炮身管存在尺寸之间的相互约束，即do3≤do2. 为了保证弹丸出射速度，身管轴向总尺寸长度是固定的，因此尺寸需满足

L2+L3≥7 050 mm.

(21)

强度约束条件为在舰炮发射过程中，其身管最大应力点处的应力σ应小于等于材料的比例极限应力σe，即

σ≤[σe].

(22)

2)本文选取舰炮身管f(X)为刚度优化指标，目标函数为f(X)和m(X). 建立抗振性能优化数学模型：

(23)

3)根据抗振性能优化数学模型(23)式，利用多目标GA进行身管抗振性能优化，得到最优解集。

4)结构参数优化后得到最优解集，在最优解集中选出一组最优解。并且，对优化后结果的合理性进行验证，若满足设定的约束条件，则结果为最终优化解，否则重新选择最优解进行验证，直至满足为止。

3.3 抗振性能优化结果分析

本文使用ANSYS软件优化计算平台，采用多目标优化GA进行抗振性能优化[15]。目标函数为f(X)、m(X)；设计变量为do2、L2、do3、L3. 约束条件为舰炮身管各段之间的尺寸约束与强度约束。多目标优化GA参数设置在此不详细说明。

通过仿真最终得到多目标优化解集，这里给出了3组最优解，每组最优解对应变量与目标数值如表4所示。

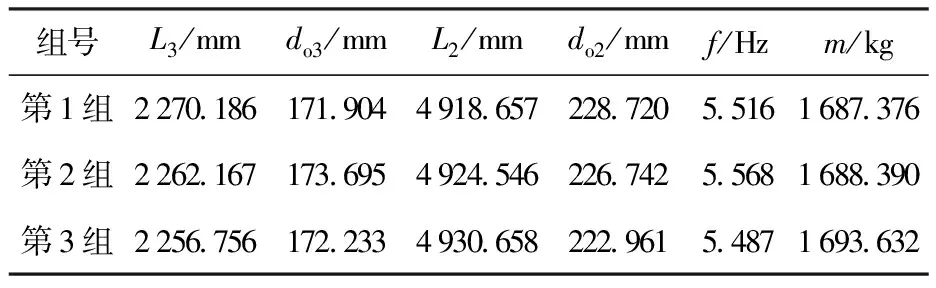
表4 数据变量优化结果

从表4可以看出，各设计变量都收敛、稳定在一定数值，目标函数值达到最优。为了确定优化效果为最好的一组，将优化前振动性能分别与3组优化后振动特性进行对比，对比结果如图6所示。

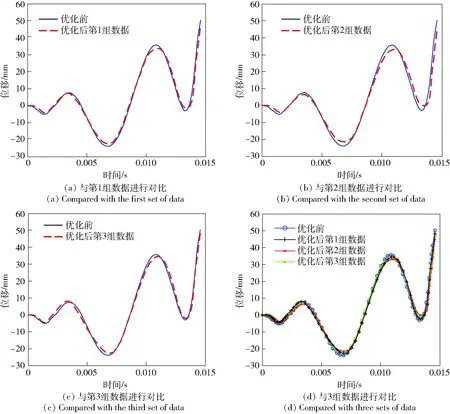
图6 舰炮身管优化前和优化后炮口振动位移对比Fig.6 Comparison of muzzle vibration displacements of naval gun barrel before and after optimization

由图6可知：优化后结构参数对振动性能有一定的抑制，但影响不是非常明显；第2组数据对应的炮口振动位移要小于其他2组，故第2组数据即为身管最终优化结果，将其数据带入基于ANSYS软件的分析模型可得到舰炮身管优化前和优化后数据，如表5所示。

由表5可见，舰炮身管抗振性能优化后，其1阶固有频率提高了17.99%、质量降低了6.12%，达到了优化目的。需要强调的是：虽然优化后的数值保留了3位小数，但在舰炮身管实际加工过程中，需根据实际要求对优化后的数值圆整处理，从而可得到整数设计变量。

表5 优化前和优化后数据对比

4 舰炮身管抗振性能优化结果有效性检验

4.1 实例验证

第2节和第3节针对3段空心阶梯悬臂梁结构身管模型分别对参数灵敏度和结构优化进行了分析，并通过舰炮身管的1阶固有频率、质量以及结构尺寸约束条件得到了一组最优解。为了进一步验证优化结果的正确性，采用如图7所示大口径舰炮身管实例验证模型。图7中：L′1、L′2、L′3为舰炮身管主要部分长度，L′1的横截面尺寸固定不变，L′2、L′3的横截面尺寸沿炮膛轴线呈线性变化；d′o1、d′o2为舰炮身管外径尺寸；L′4为舰炮身管药室部分长度，其大小决定了药室空间大小；结构优化设计忽略了膛线对质量、刚度与强度的影响，故图7中未标出膛线。

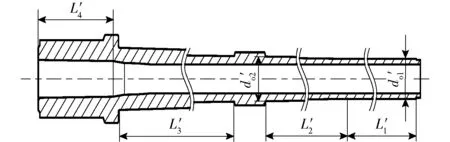
图7 舰炮身管实例验证模型Fig.7 Example verification model of barrel

身管物理特性参数：弹性模量为2.1×1011MPa，泊松比为0.27，密度为7 800 kg/m3，材料比例极限为1 030 MPa，安全系数为1.3，优化前质量为1 852.8 kg. 身管验证模型优化过程同第3节。

4.1.1 确定参数设计优化变量

由图7实例模型可知，结构参数优化变量包括L′1、L′3、L′4、d′o1、d′o2.

4.1.2 确定身管优化约束条件

根据大口径舰炮身管实际使用需求，L′1、L′3、L′4、d′o1、d′o2的结构尺寸约束范围为

(28)

(24)式中，舰炮身管存在尺寸之间的相互约束，即d′o2≤d′o1. 强度约束条件为

σ≤[σe].

(25)

4.1.3 确定优化目标函数

优化目标是为了提高刚度、降低质量，目标函数为f(X)、m(X). 建立实例验证模型身管的抗振性能优化数学模型：

(26)

4.2 实例验证优化结果

选取最终得到的50组多目标优化解集连成曲线，如图8所示。从50组种群中选取9组最优解，每组最优解对应设计变量及目标函数值如表6所示。

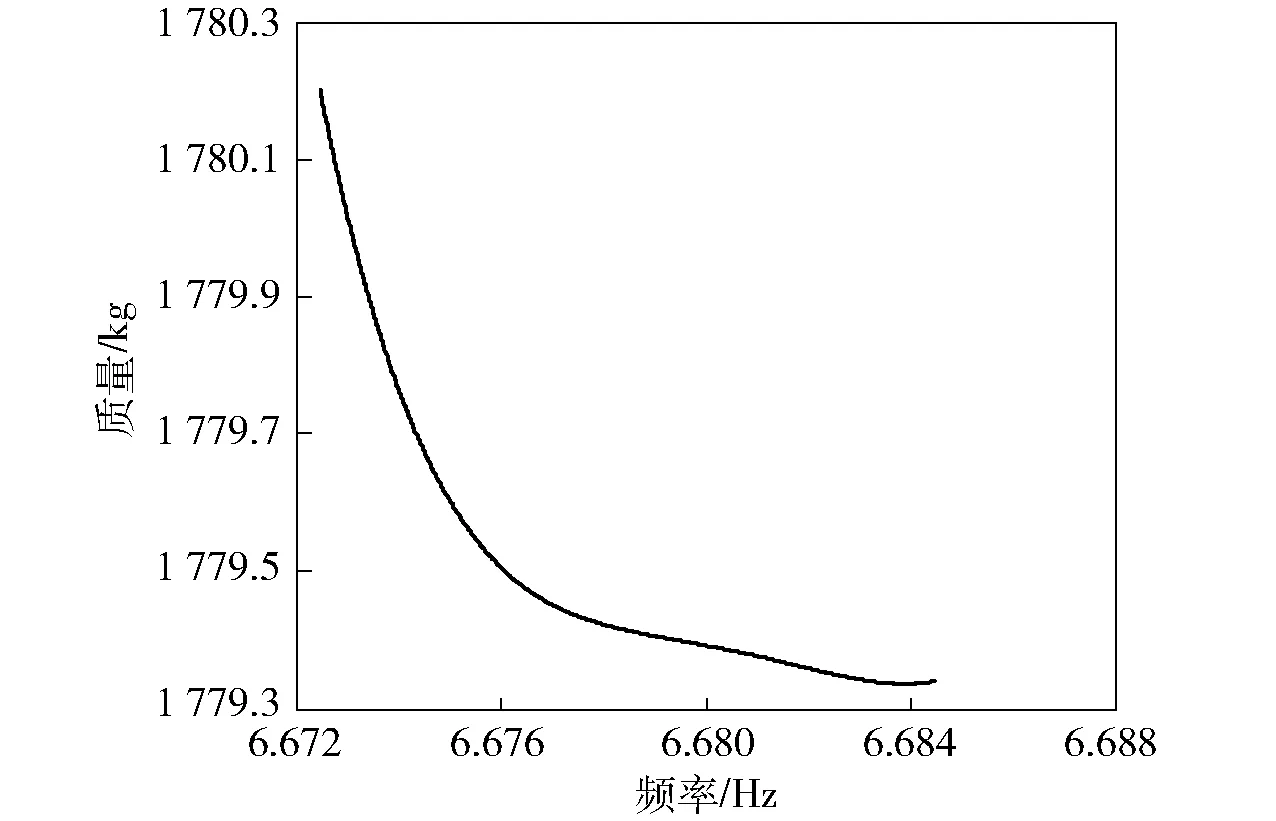
图8 多目标优化解集Fig.8 Multi-objective optimization solution sets

由表6可见，各个设计变量都收敛、稳定在一定数值，目标函数值达到最优。对比9组最优解所对应的目标函数值可知，第1组最优解对应的1阶固有频率最大、质量最小，故优化后的最优解

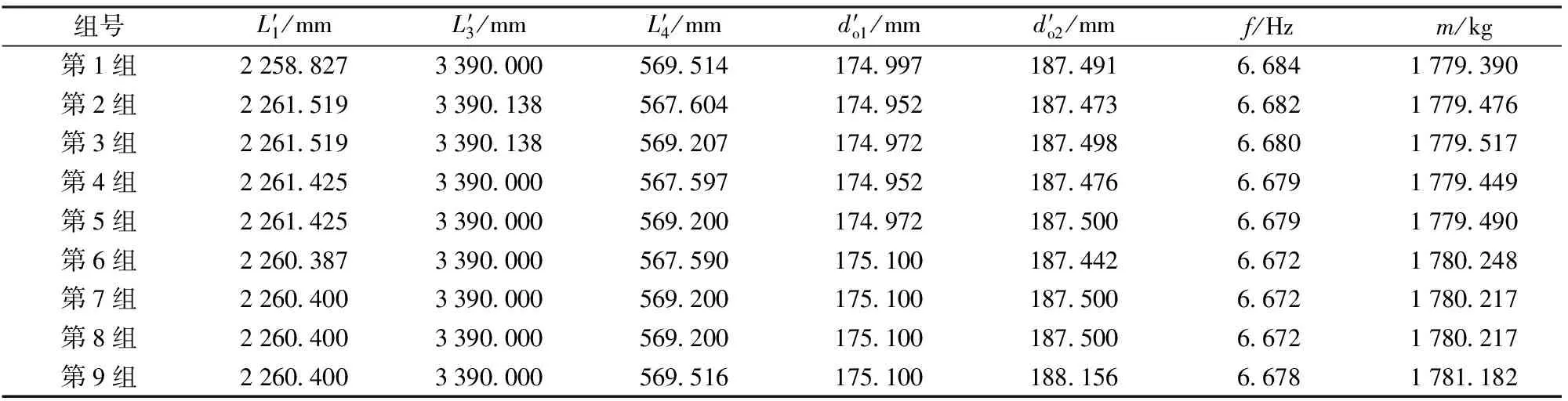
表6 每个最优解对应的目标函数值及变量值

为第1组。将第1组最优解带入上述优化过程，得到优化前和优化后数据对比，如表7所示。

由表7可见，优化后的1阶固有频率提高0.304 Hz，质量降低73.41 kg. 1阶固有频率优化效果不明显，原因在于各设计变量变化范围过小，同时身管总长过长。而质量优化效果相对较好，达到优

表7 优化前和优化后数据对比

化目的。

4.3 1阶固有频率和质量优化结果对比分析

4.3.1 主要参数对比分析

对比1阶固有频率优化模型和质量优化模型，其主要结构参数设计变量几乎相同。其中：do2与do3分别对应验证模型d′o2与d′o1；L3对应L′1；L2对应L′2和L′3. 具体参数如表8所示。

4.3.2 模态与固有频率对比分析

通过表8可以发现，关键结构参数优化得到的数值基本相同，因此可以说明第1节简化模型及优化结果是正确的。

舰炮身管优化不仅可以使1阶固有频率增大、质量减小，还会使身管各阶固有频率及振型发生变化。需要说明的是：舰炮身管模态分析过程中，一般不会发生高阶固有频率共振的现象，故这里主要对前6阶模态进行了对比分析。根据模态分析理论，结构模态分析一般是指在线性条件下研究其动态特性，在分析过程中忽略非线性因素对结构本身模态的影响。舰炮身管模态分析考虑了自身结构与安装约束条件的影响，主要过程与身管优化过程相似。按照上述要求进行模态分析，分别得到了简化模型与实例验证模型优化前和优化后的前6阶固有频率f1、f2、f3、f4、f5、f6，如表9所示。

由表9可见，优化后各阶固有频率均提高了一定数值，但提高幅度有限，原因在于身管长径比较大，并且优化后也不会大幅度改变身管长径比[16]。同时，对比简化模型与实例模型的各阶固有频率，数值大小比较接近，没有出现固有频率失真现象，因此可说明简化模型的优化结果对于实际设计来说具有一定参考价值。