基于激波传播路径的弹头斜入射双三角阵定位模型

林逸雪， 狄长安， 狄长春， 宫新宇， 计寒

(1.南京理工大学 机械工程学院, 江苏 南京 210094；2.陆军工程大学石家庄校区 火炮工程系， 河北 石家庄 050003；3.白城兵器试验中心， 吉林 白城 137001)

0 引言

实弹射击是部队重要的训练项目，在实弹射击中，弹头命中率是衡量部队射击水平的重要指标。在武器系统性能评估中，立靶密集度是评估枪炮等军事武器性能的关键指标，因此获取精确的弹着点位置信息十分重要。声定位作为一种可重复使用且成本低廉的非接触式测量方法，以其结构简单、可靠性高、可抗电子干扰、可昼夜全天候工作等优点，广泛用于弹着点测量[1]。目前常用的声学立靶声阵列模型有四点阵、八点线阵、八点圆阵、多点圆阵[2]和双三角阵，其中双三角阵因有效靶面面积大、可靠性高、采用地面安装方式、使用便捷、安全性好等优点，常用于大靶面的弹头坐标测量。传统的双三角阵定位模型利用到达时间差(TDOA)法[3-4]列出非线性方程组，并通过最小二乘法求解出弹着点坐标。但传统声靶模型中的时间差是假设弹头垂直入射靶面，激波以视速度沿靶面传播到各传感器得到的，而实际射击时弹头无法与靶面垂直，导致理论时差与实际时差不符，不可避免地对定位精度造成了影响。

为了减小传统声定位模型由于弹头斜入射造成的弹着点坐标测量误差，文献[5]利用圆盘阵列的几何关系求解入射方向的投影与靶面的夹角即偏航角，利用求解的偏航角修正时延偏差，从而提高声靶定位精度。文献[6]基于开放式T靶分析研究了弹头斜入射时方位角对定位精度的影响，提出一种针对方位角的弹头斜入射定位模型，并未考虑弹头的俯仰角；文献[7]通过设置虚拟靶面将弹头实际斜入射转换为垂直入射靶面的方法，给出一种基于立体阵的弹头斜入射测试模型，但未考虑激波衰减对定位精度的影响；文献[8]分析了弹头斜入射俯仰角和偏航角对双三角阵声定位系统定位精度的影响，但未给出弹头斜入射定位误差有效修正方法。因此建立一种能修正入射角引入的定位误差且适用于双三角阵的弹头斜入射的声定位模型，对提高声定位系统精度和适用范围具有重要的现实意义。

本文基于双三角声阵列立靶测量时弹头斜入射靶面的激波传播路径，提出一种新型弹头斜入射定位模型，并针对传统双三角阵定位模型中弹头非垂直入射引起的斜入射误差问题，对比分析了俯仰角及偏航角对新旧模型定位精度的影响，并进行了实弹射击实验验证。实验结果表明，斜入射模型与传统模型相比，可明显降低斜入射误差，并且还能给出弹头的入射俯仰角和偏航角。

1 立靶测量弹头激波传播路径

弹头在超音速飞行过程中，气流以超音速吹过弹头被弹头头部分开，使弹头周围气体发生压缩和膨胀、形成激波，由于弹头激波信号曲线呈N形，激波又被称为N波[9]。

弹头飞行过程中，在某点处产生的激波会以该点为球心以速度vs沿球面向外传播。飞行的弹头可以近似看作为一个移动的点声源，其在弹道线上各点处会产生多个激波球面，由于弹头飞行速度大于声速，多个激波球面将会结合形成一个激波圆锥体，激波波阵面则沿着圆锥面法线方向以速度vs向外运动。弹头激波传播特性如图1所示，图1中：vb为弹头飞行速度，vs为激波传播速度，c为声速，β=arcsin(c/vb)为激波圆锥半角。

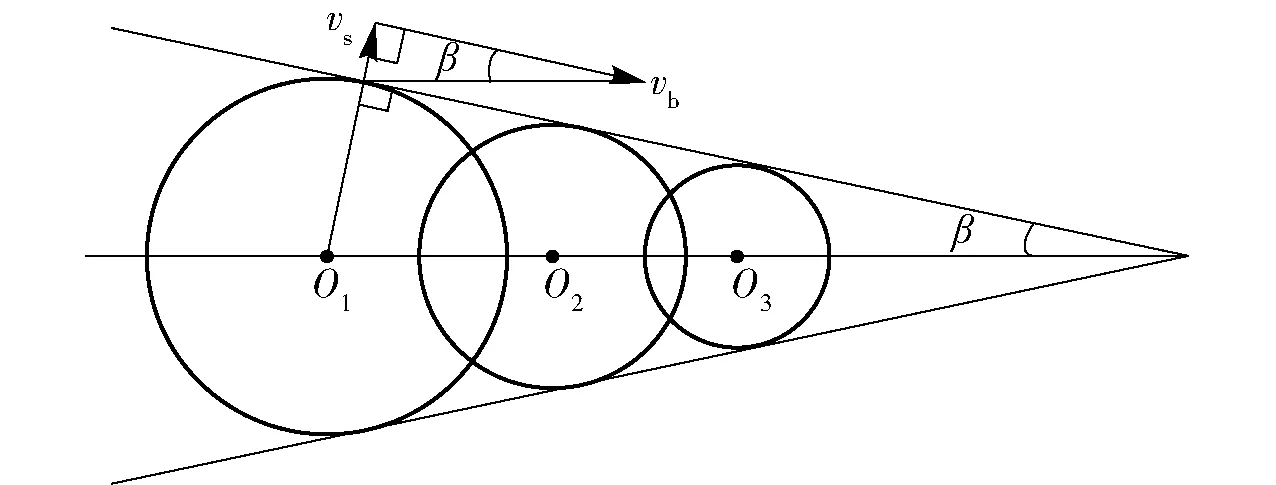
图1 弹头激波传播特性Fig.1 Projectile shock propagation characteristics

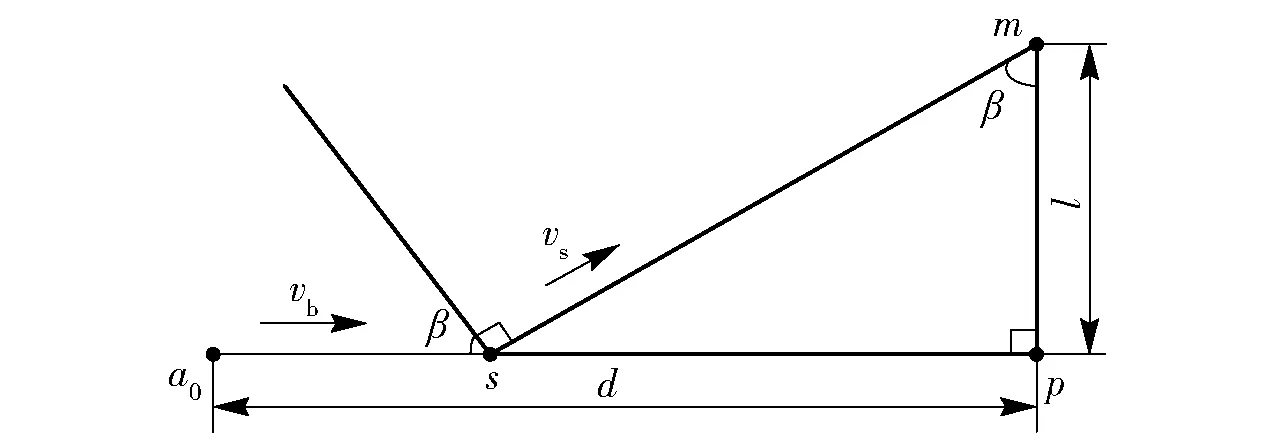
图2 弹头激波传播路径示意图Fig.2 Schematic diagram of projectile shock propagation path

设在弹头弹道线附近有一个传声器m，根据弹头激波传播特性，在弹头弹道线上必存在一个点s，弹头在该点处产生的激波最早被传声器m接收，弹头激波传播路径如图2所示，图2中：a0为弹头起始位置，p为弹头弹着点，d为弹头飞行距离，l为传声器m到弹着点p的距离。根据模型几何关系可得激波到达传声器的时间为

(1)

式中：tb为弹头飞行时间；ts为激波传播时间。

2 弹头斜入射模型及误差分析

2.1 弹头斜入射双三角阵模型

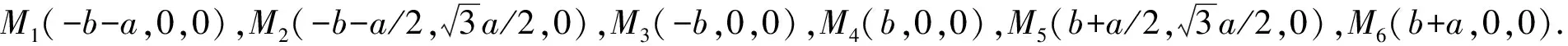
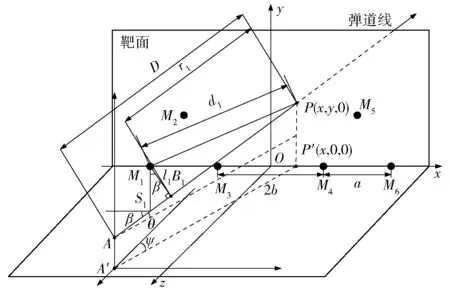
图3 弹头斜入射定位模型示意图Fig.3 Schematic diagram of projectile oblique penetration positioning model

根据激波传播路径，弹头在弹道线上点Si处产生的激波最早被Mi接收，点Bi为传感器Mi在弹道线上的投影，设PBi的长度为ri，根据同一直线上两点坐标关系，点Bi(xBi,yBi,zBi)的坐标可由下式表示：

(2)

在△BiPMi中BiP⊥BiMi，则

(3)

整理(3)式可得

ri=(x-xi)cosθsinψ+(y-yi)sinθ.

(4)

设PMi长度为di，MiBi长度为li，AP长度为D，则

(5)

在直角三角形△PMiBi中，根据勾股定理可得

(6)

根据(1)式可知弹头激波到达传声器Mi的时间为

(7)

整理得

(8)

设弹头激波到达传声器Mi与Mj间的时间差值为tij(j=2，3，4，5，6,i≠j)，由(8)式可得

(9)

传统的声靶定位模型中，一般将激波传播速度vs作为恒定值代入公式中来计算，但实际上，声速在大气中传播时还受到压力和温度的影响。而激波是一种压力波，其压力幅值与传感器到弹道线距离的3/4方呈反比，且与运动物体的形状系数、周围大气压力、马赫数(物体运动速度与声速之比)、运动体直径和运动体长度等有关[10]。根据激波衰减特性可知，激波传播速度vsi会随着传播距离的增加逐渐减小，即激波传播速度与传声器到弹道线的距离有关[11]：

(10)

式中：k为激波速度衰减因子，与弹头直径有关。

根据双三角阵定位原理，结合(2)式～(10)式可得到弹头斜入射定位模型：

(11)

弹头斜入射定位模型为一个非线性方程组，包含15个独立方程，由(2)式～(4)式可知，方程组中的参量包括x、y、xi、yi、θ、ψ、β、vb和tij，其中xi、yi、β、vb和tij为已知量，x、y、θ、ψ为待求解量，采用最小二乘法求解定位模型方程组可以得到弹头弹着点坐标P(x,y)以及弹头入射时的俯仰角θ、偏航角ψ.

2.2 声阵列模型误差仿真分析

为了验证弹头斜入射双三角阵定位模型相比传统双三角阵模型定位更精确，利用MATLAB软件对该模型进行了仿真计算。由于双三角阵声靶靶面关于y轴对称，针对靶面第1象限内的的5 m×5 m测试区域进行仿真计算，选择x轴正方向上的0～5 m、y轴正方向上的2～7 m区域。

因为实际射击中一般采用平射，弹头斜入射角度很小，所以主要针对小入射角度对定位精度的影响进行分析。假设vb和vs恒定不变，设定俯仰角θ和偏航角ψ为0～1.5°，间隔为0.3°，代入模型中由MATLAB软件计算得到仿真结果并绘制误差分布图。图4为入射角对定位精度的影响，图5为5 m×5 m靶面内斜入射模型和传统模型的平均定位误差、最大定位误差受俯仰角θ、偏航角ψ变化的影响。

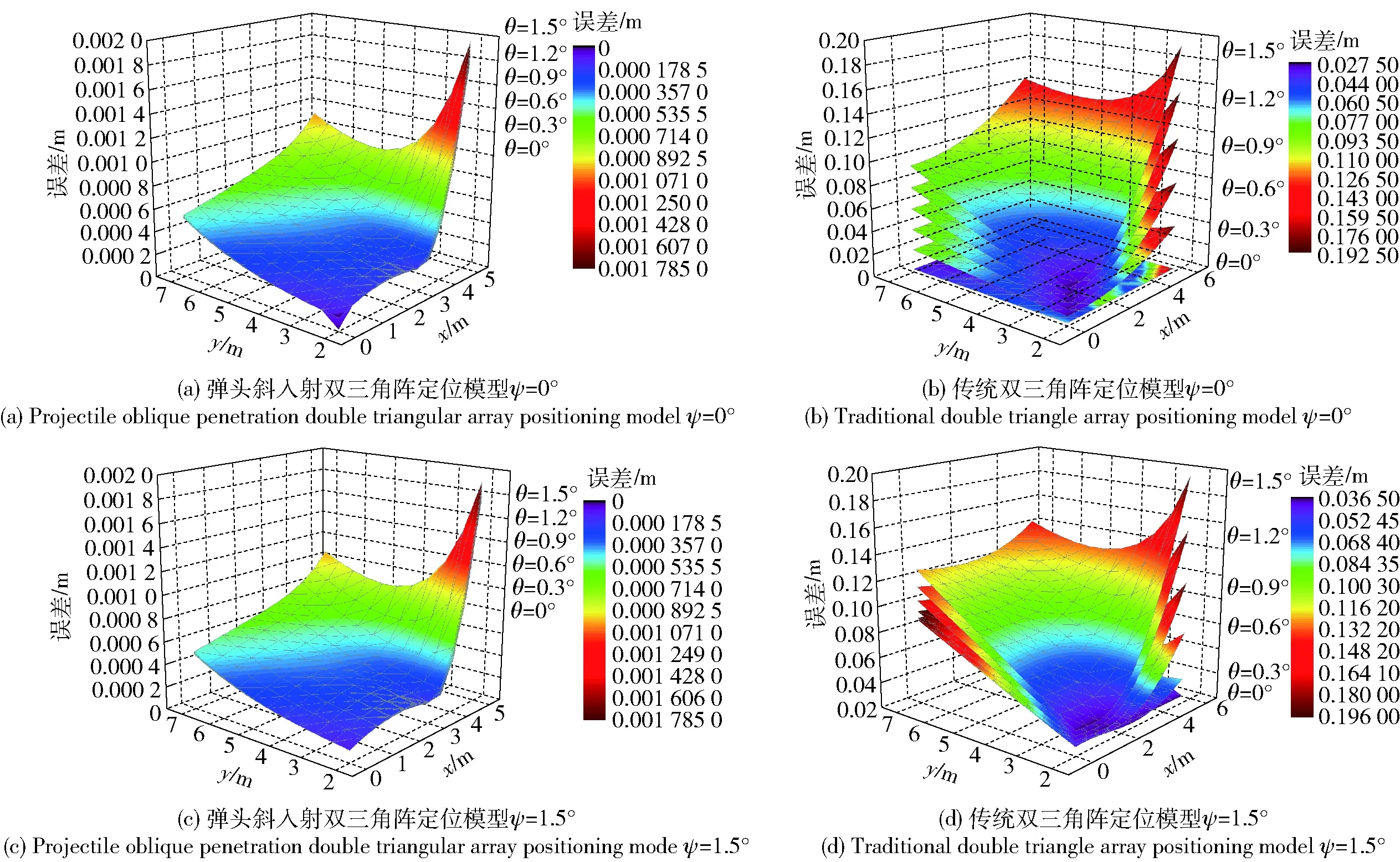
图4 入射角对定位精度的影响Fig.4 Influence of penetration angle on positioning accuracy

由图4和图5可以看出：斜入射模型由于考虑了俯仰角及偏航角的影响，对斜入射引起的定位误差有明显抑制作用，而传统模型中定位误差随着入射角增大而明显增大，且其中俯仰角θ对定位精度的影响较偏航角ψ更大。

3 实验结果及分析

为了验证本文构建的弹头斜入射定位模型相对传统模型定位精度更高，并且能有效地计算出弹头斜入射情况下的弹着点坐标及入射角，在室内靶道进行了实弹射击实验。本次实验坐标测量装置采用的双三角阵声靶的靶面参数为a=0.3 m，b=0.7 m，在声靶后方垂直竖立一张2 m×2 m标准测试靶板(测量精度为1 mm)用于人工测量弹着点坐标，弹头采用5.8 mm步枪弹，室内环境无风。实验时射击起始位置距靶面约20 m，利用弹道垂直控制方法及装置调整靶架位置后，分别瞄准纸靶上预设的多个瞄准点进行多组实弹小角度(±2°范围内)斜入射靶面射击，弹头飞行速度为800 m/s. 分别使用传统双三角阵定位模型和弹头斜入射定位模型计算弹着点坐标并与纸靶测量坐标进行对比，部分实验数据如表1所示。

从表1数据可以看出弹头斜入射定位模型计算的弹头俯仰角和偏航角基本上在±1.4°范围内，符合弹丸射击实际情形(±2°范围内小角度射击)，且弹着点x、y坐标与纸靶坐标基本一致，验证了该模型的可行性。通过对比表1中传统双三角阵模型及弹头斜入射模型计算坐标数据可以得出：传统双三角阵定位模型计算的弹着点坐标在x轴、y轴方向上的误差均不大于1.6 cm，最大定位误差ΔR为2.04 cm，平均定位误差为1.44 cm；弹头斜入射模型计算的弹着点坐标在x轴、y轴方向上的误差均不大于1 cm，最大定位误差ΔR为1.15 cm，平均定位误差为0.82 cm，相比前者减小了0.62 cm，即相比传统双三角阵定位模型误差减小了43.46%，具有更高的定位精度。

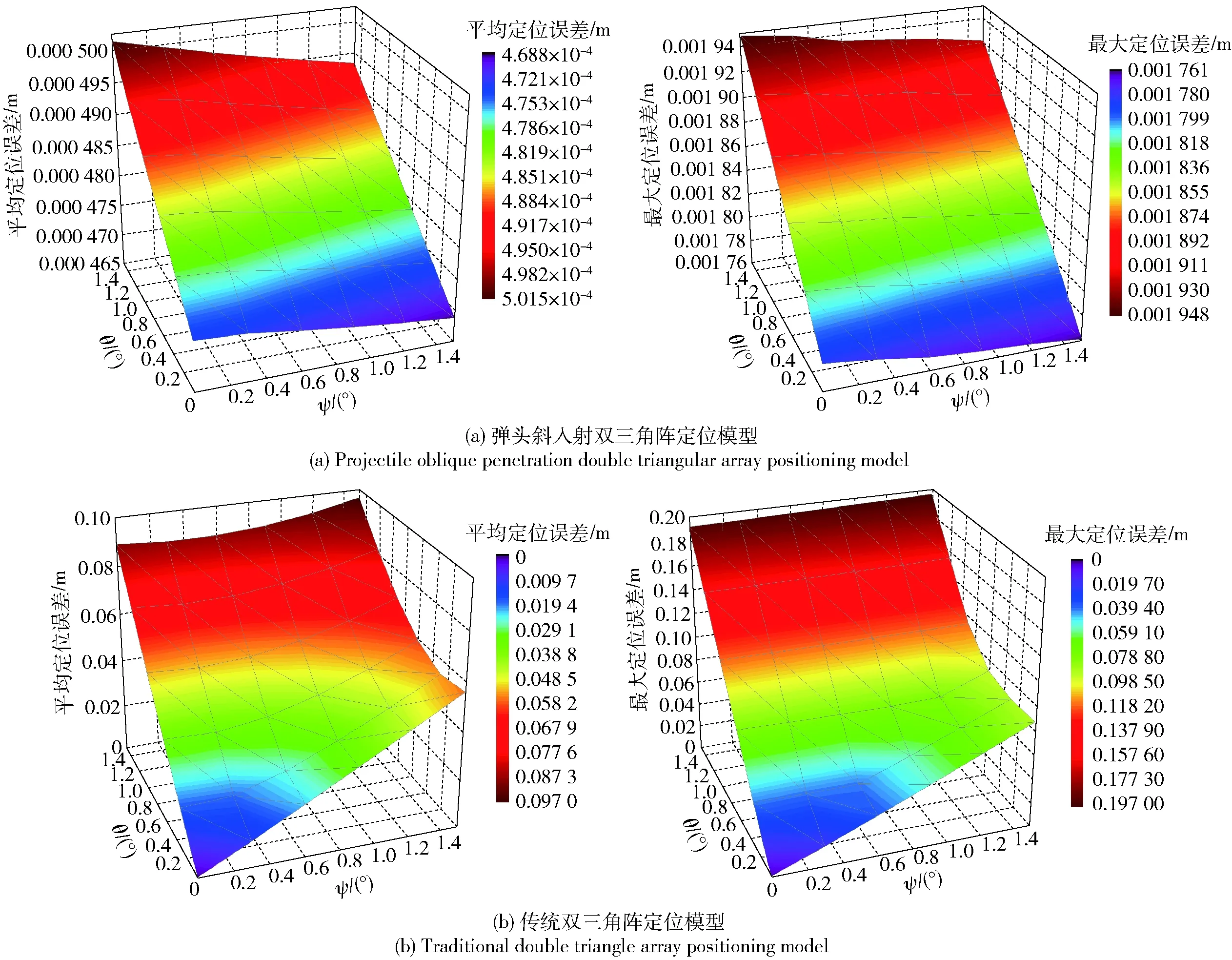
图5 定位误差受入射角影响变化趋势图Fig.5 Position error vs. penetration angle

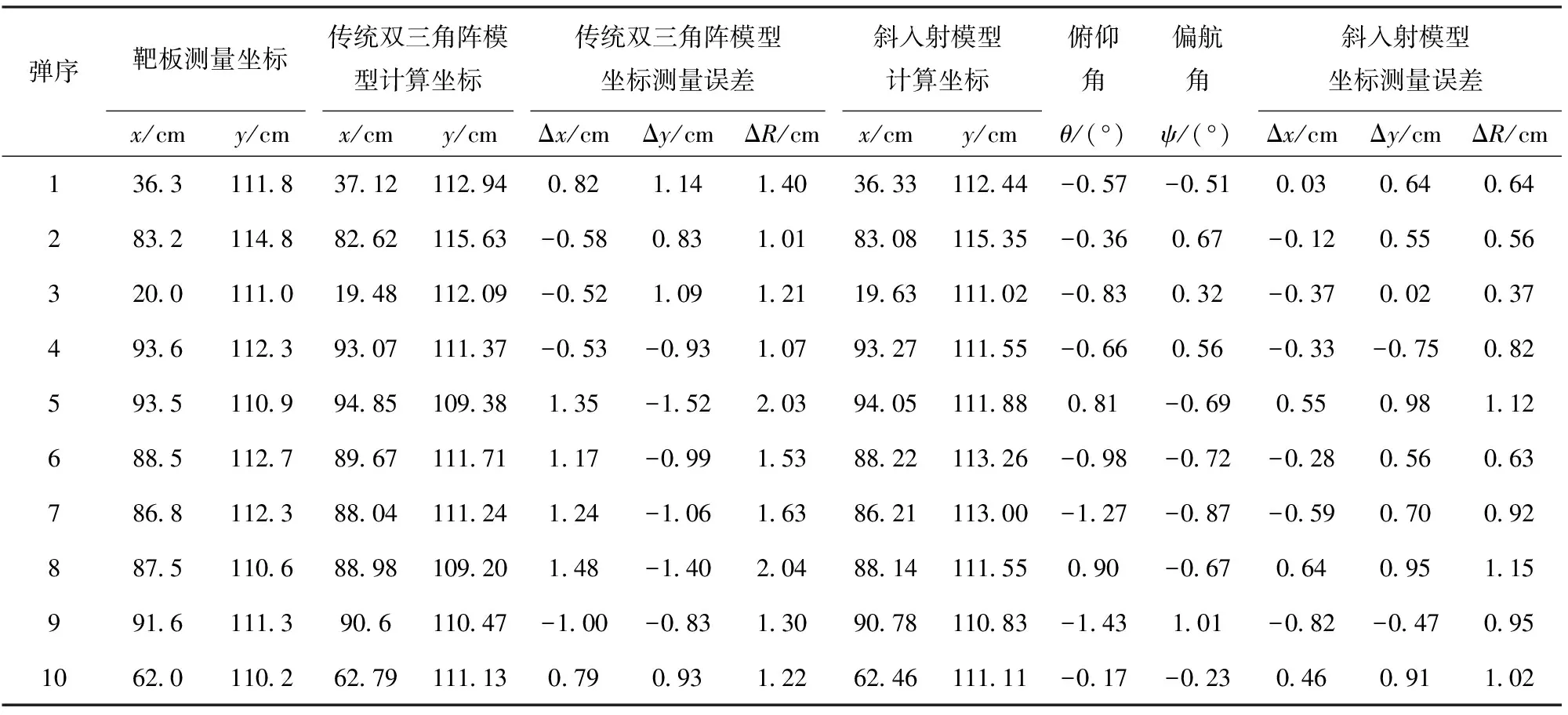
弹序靶板测量坐标传统双三角阵模型计算坐标传统双三角阵模型坐标测量误差斜入射模型计算坐标俯仰角偏航角斜入射模型坐标测量误差x/cmy/cmx/cmy/cmΔx/cmΔy/cmΔR/cmx/cmy/cmθ/(°)ψ/(°)Δx/cmΔy/cmΔR/cm136.3111.837.12112.940.821.141.4036.33112.44-0.57-0.510.030.640.64283.2114.882.62115.63-0.580.831.0183.08115.35-0.360.67-0.120.550.56320.0111.019.48112.09-0.521.091.2119.63111.02-0.830.32-0.370.020.37493.6112.393.07111.37-0.53-0.931.0793.27111.55-0.660.56-0.33-0.750.82593.5110.994.85109.381.35-1.522.0394.05111.880.81-0.690.550.981.12688.5112.789.67111.711.17-0.991.5388.22113.26-0.98-0.72-0.280.560.63786.8112.388.04111.241.24-1.061.6386.21113.00-1.27-0.87-0.590.700.92887.5110.688.98109.201.48-1.402.0488.14111.550.90-0.670.640.951.15991.6111.390.6110.47-1.00-0.831.3090.78110.83-1.431.01-0.82-0.470.951062.0110.262.79111.130.790.931.2262.46111.11-0.17-0.230.460.911.02

4 结论

本文针对传统双三角阵模型未考虑入射角对测量弹头弹着点坐标信息的影响的问题，提出了一种基于激波传播路径的弹头斜入射双三角阵定位模型，并对引入的时延误差进行修正，提高了坐标测量精度。为了验证本文提出的弹头斜入射定位模型，在靶场进行了实弹射击对比实验，实验结果表明，相对于传统双三角阵定位模型，弹头斜入射定位模型有效地修正了斜入射误差，在2 m×2 m靶面内坐标测量误差均小于1 cm，具有更高的定位精度。