固定鸭舵导引组件修正力模型改进及参数辨识
2019-03-13冯斌于纪言王钰王晓鸣鞠潭
冯斌, 于纪言, 王钰, 王晓鸣, 鞠潭
(南京理工大学 智能弹药技术国防重点学科实验室, 江苏 南京 210094)
0 引言
弹道修正弹的弹道预测和修正指令的生成均需要准确的气动力数据,而将弹丸受到的气动力与弹丸状态参数联系起来建立气动力模型,可以为弹丸气动外形设计、弹道设计以及弹丸飞行性能分析提供帮助。固定鸭舵双旋修正弹将带有固定鸭舵的修正组件(见图1)和弹体在旋转通道解耦,弹体的高速旋转保证飞行稳定,修正组件低速转动,调节由舵面产生的修正力方向,从而实现弹道修正。建立准确的导引组件修正力气动工程模型对于修正弹飞行特性研究具有重要意义。
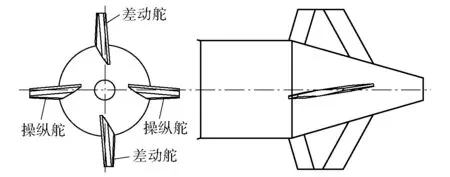
图1 4°舵偏固定鸭舵双旋修正弹修正组件模型Fig.1 Dual-spin projectile correction kit with 4° canard deflection
目前,国内外对双旋弹道修正弹的气动特性研究主要从数值计算和风洞试验两个方面进行。Jermey[1]采用风洞试验对带鸭舵的弹丸进行测力试验。吴萍等[2]通过风洞试验方法对带鸭舵的弹丸气动特性随马赫数、攻角以及舵偏角的变化规律进行了研究。SAHU等[3-4]采用非结构嵌套网格的方法实现了多自由度模拟飞行,为本文计算方法的选取提供了参考。纪秀玲等[5]通过数值计算研究了隔转鸭舵双旋弹纵向气动特性,通过数值仿真得出鸭舵相位角和全弹法向力、俯仰力矩变化呈三角函数关系的结论。许安勇[6]也进行了相应数值研究,通过计算弹丸各修正状态的陀螺稳定因子和动态稳定因子,得出弹丸各修正状态均具有良好飞行稳定性的结论。Liang等[7]将优化算法与数值计算结合起来,对固定鸭舵双旋修正弹的鸭舵外形进行优化。殷婷婷等[8]对固定鸭舵导引组件的控制模型进行了创新,提出了一种结合数值仿真和试验测试的建模方法,通过将修正组件置于自由射流风洞中对模型进行验证。程杰等[9]基于小扰动理论建立的关于双旋修正弹工程模型应用较为广泛。该模型将修正组件的4片固定鸭舵舵片分为提供修正侧向力的操纵舵舵片和提供组件反转力矩的差动舵舵片两组。基于小扰动理论将每组舵片的气动力分解为受横向绕流产生的攻角效应和受轴向绕流产生的舵偏效应。模型相关参数利用风洞试验得到的数据进行参数辨识和验证,但是以两组舵片受力叠加方式仍存在无法精确表示导引组件的修正力问题。根据其模型可知导引组件的修正力在只存在于垂直操纵舵舵片的方向,但是客观物理现象是存在攻角时,迎风侧与背风侧舵片受力差异导致差动舵舵片也能产生修正力。
因此,本文基于小扰动理论分别考虑4片舵片气动力建立导引组件的修正力气动工程模型,并对工程模型中的相关参数使用Levenberg-Marquardt(L-M)算法[10]进行辨识。准确的导引组件修正力模型建立为后续通用性研究和修正弹飞行特性的研究奠定了基础。
1 数值方法验证
本文基于气动力数据进行双旋修正弹导引组件气动工程模型的建立和参数辨识,由于风洞试验六分量天平能测得全弹气动力,但无法直接获得导引组件部分气动力,因此还需要依靠计算流体力学(CFD)方法获得更详细的导引组件部分气动力。在此之前,通过对比风洞试验六分量天平测得全弹气动力数据和数值计算得到的全弹气动力结果,验证数值计算的有效性。
1.1 风洞试验
风洞试验在南京理工大学HG04超声速风洞中进行。HG04风洞为直流下吹暂冲式闭口跨超声速风洞, 采用固块式二元喷管,可以通过更换不同喷管来改变马赫数,试验段横截面面积为0.3 m×0.3 m,试验段长0.6 m. 在试验段两侧开有光学玻璃观察窗,尺寸为0.29 m×0.16 m,便于在试验过程中观测模型姿态或进行纹影照相。试验模型及其在风洞中的安装如图2和图3所示。

图2 风洞试验所用模型Fig.2 Model for wind tunnel experiment

图3 试验模型在风洞中的安装图Fig.3 Physical model mounted in wind tunnel
1.2 数值计算以及结果对比
为了验证数值计算方法的有效性,需对双旋弹所在计算域进行三维建模和空间离散。图4所示为4°舵偏的双旋弹计算域网格,计算域按照空间分布,分解为鸭舵绕流区、弹体绕流区和外部流场。对计算域进行空间离散生成非结构六面体单元计算网格。图5所示为4°舵偏的双旋弹弹体表面网格。
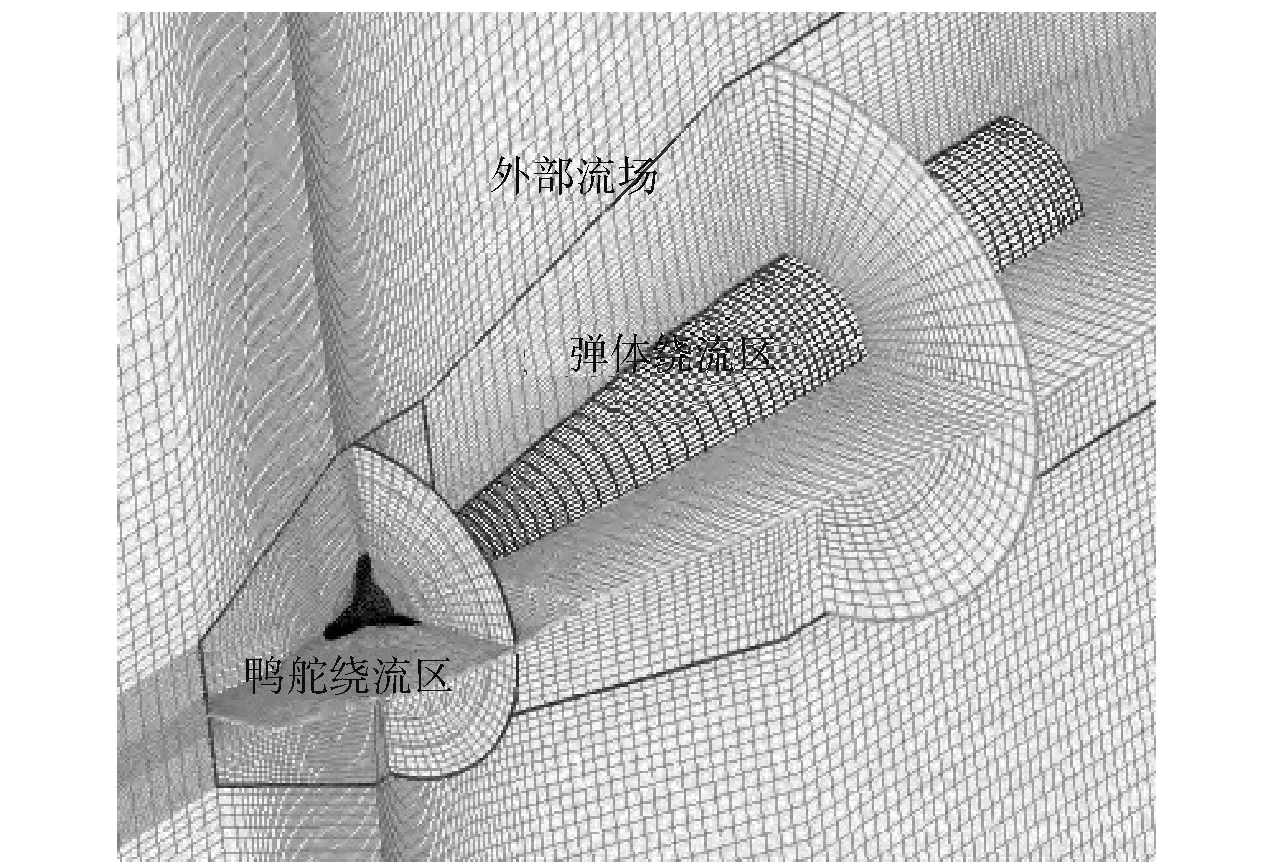
图4 计算域网格Fig.4 Grid of computational domains

图5 弹体表面网格Fig.5 Grid of projectile surface
迭代计算中,使用密度基求解器对流项使用Roe通量差分格式离散,梯度使用最小二乘法求解,其他流动变量使用2阶迎风格式离散。分别引入Spalart-Allmaras(S-A)湍流模型和剪切压力传输(SST)k-ω湍流模型使控制方程组封闭。流场入口边界使用压力远场条件,出口使用压力出口,双旋弹弹体表面使用无滑移壁面条件。计算马赫数分别为1.5、2.0、2.5、3.0、3.5和4.0,攻角分别为0°、4°时全弹模型受力情况。
数值计算结果和风洞试验结果的阻力系数、升力系数对比如图6所示。对于有攻角、无攻角两种工况下,两种气动力系数的计算值和试验值具有相同变化趋势。阻力系数计算值与试验值相对误差小于13%(见图6(a)),升力系数计算值相对误差小于12%(见图6(b)). 对于工程应用,其相对误差值处于可接受范围。通过对比S-A湍流模型和SSTk-ω湍流模型的计算结果可以看出,两种湍流模型结果高度一致。因此,在数值计算中选择计算成本较低的单方程S-A湍流模型。
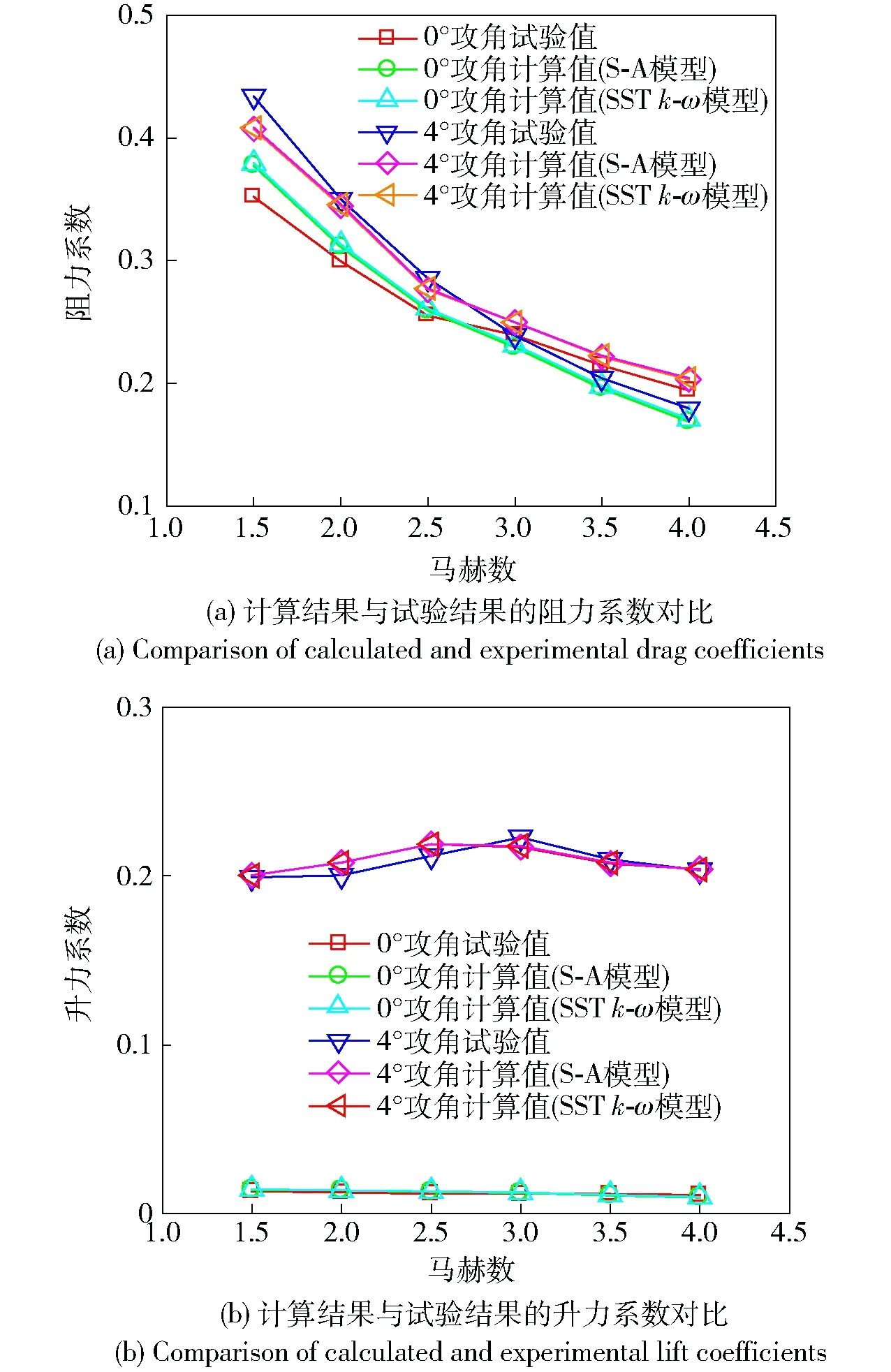
图6 计算结果与试验结果的气动力系数对比Fig.6 Comparison of calculated and experimental aerodynamic coefficients
2 修正力气动工程模型的建立
固定鸭舵双旋修正弹通过导引组件转动来改变修正力方向,从而改变全弹动力平衡角,实现弹道修正。固定鸭舵修正组件产生的修正力来自4片舵片,因此对于4片舵片产生的修正力进行精确建模有助于后续的通用性和修正弹飞行特性研究。
在建立气动工程模型之前,先建立弹体坐标系,原点O取在全弹质心,x轴与弹轴重合指向弹尾方向,y轴垂直于x轴指向上方,z轴与Oxy平面垂直。根据细长体理论,在小攻角、小舵片偏角、薄弹翼条件下,将固定鸭舵双旋修正弹导引组件的小扰动流场简化成由修正弹攻角产生横向绕流的攻角效应(见图7(a),γp为舵片相位角)以及由舵偏角产生的舵偏效应(见图7(b),δd为差动舵舵片舵偏角,δm为操作舵舵片舵偏角)两种效应的叠加。因此,分别单独考虑任意相位角γp两种效应的作用,然后将结果线性叠加得到修正力的工程模型。
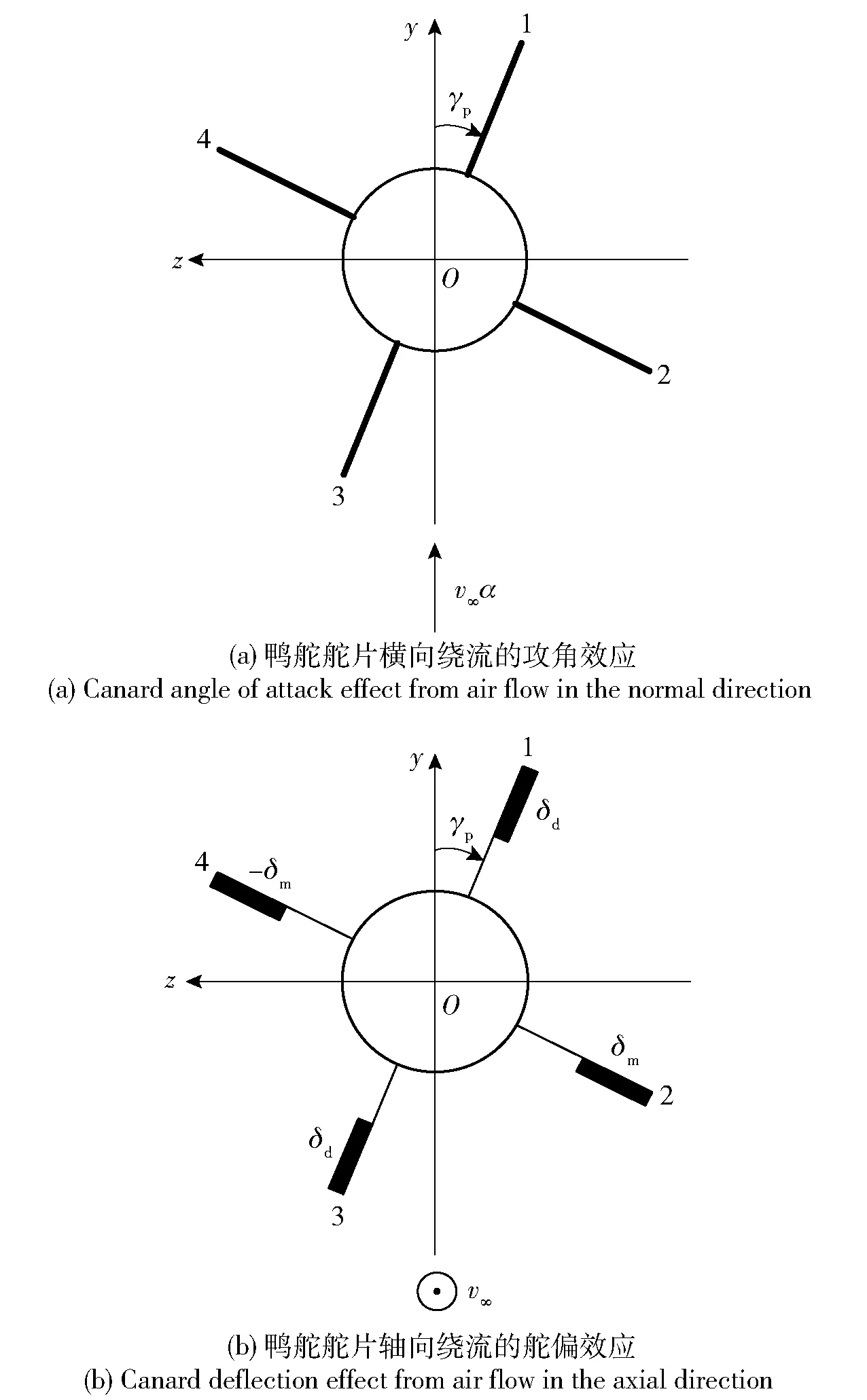
图7 鸭舵舵片绕流示意图(弹尾视图)Fig.7 Air flow in the normal and axial directions (view from the rear of canard)
2.1 攻角效应的修正力
如图7(a)所示“X”形气动布局,以舵片1为例,与攻角平面的夹角为γp,设攻角为α,将来流速度分解为平行弹轴速度分量v∞cosα≈v∞和垂直弹轴速度分量v∞sinα≈v∞α. 前者与舵片平面平行,对于薄舵片不产生升力;后者为升力主要来源。v∞α分解为垂直舵片1分量v∞αsinγp和平行舵片1分量v∞αcosγp,前者为舵片1产生法向力主要成因,因此舵片1有效攻角αe=αsinγp. 规定垂直舵片面指向逆时针方向的法向力为正,综上所述,舵片1由攻角效应产生的法向力表达式为
(1)
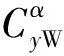
同理,其他3片舵片的法向力表达式依次为
(2)
(3)
(4)
将舵片1所受法向力分解到y轴和z轴方向,得到舵片1产生的y轴方向侧向力Fyα1和z轴方向侧向力Fzα1如(5)式和(6)式所示:
(5)
(6)
同理,其他3片舵片分解后所得侧向力分别为Fyα2、Fzα2、Fyα3、Fzα3、Fyα4、Fzα4.
文献[9]建立的模型中,攻角效应的修正力为各舵片修正力的直接叠加,并乘以攻角效应下弹头部对鸭舵舵片升力的干扰系数Kα,其公式如(7)式[9]所示:
(7)
本文综合考虑导引组件回转体部分对舵片受力的影响,每片舵片的y轴和z轴方向侧向力并不能直接相加,攻角效应的修正力表达式为
(8)
式中:Kα1、Kα2、Kα3、Kα4分别为攻角效应下弹头部对鸭舵舵片1、舵片2、舵片3、舵片4法向力的干扰系数。(8)式也可写成以下矩阵形式:
(9)
利用(10)式将气动力F除以动压q∞和鸭舵舵片参考面积SW换算为气动力系数C,
(10)
同理可得到鸭舵舵片攻角效应产生的修正力系数表达式为
(11)
2.2 舵片偏效应的修正力
如图7(b)所示,只有舵片偏效应中,鸭舵舵片在轴向流的作用下,由舵偏角δd、δm产生法向力。4片舵片法向力表达式分别为
(12)
(13)
(14)
(15)
与2.1节同理,将4片舵片产生的升力在y轴、z轴方向进行分解,得到4片舵片在y轴、z轴方向的修正力分量分别为Fyδ1、Fzδ1、Fyδ2、Fzδ2、Fyδ3、Fzδ3、Fyδ4、Fzδ4.
文献[9]建立的模型中,舵偏效应的修正力为各舵片修正力的直接叠加,并乘以舵偏角效应下弹头部对鸭舵舵片升力的干扰系数Kδ,其公式如(16)式[9]所示:
(16)
本文考虑导引组件回转体部分对舵片受力的影响,舵偏效应修正力的表达式为
(17)
式中:Kδ1、Kδ2、Kδ3、Kδ4分别为舵偏角效应下弹头部对鸭舵舵片1、舵片2、舵片3、舵片4法向力的干扰系数。
同理,利用(10)式可得舵偏效应产生的修正力系数为
(18)
将由攻角效应产生的修正力与舵偏效应产生的修正力相叠加即可得到导引组件的修正力气动工程模型:
(19)
(20)
文献[9]建立气动模型表达式为
(21)
(21)式仍具有缺陷,如当相位角γp=0°时,z轴方向侧向力为0,但是数值计算结果显示上、下两片差动舵舵片由于弹体迎风侧、背风侧的差异,会存在z轴方向侧向力,如马赫数为2.5,攻角为8°,γp=0°时,差动舵舵片产生的z轴方向侧向力为-16.71 N. 本文提出的分别考虑4片舵片的修正力模型可以解决这种缺陷。
3 数值计算与参数辨识
建立双旋弹导引组件修正力气动工程模型过程中,考虑了弹头对舵片升力的干扰系数Kα、Kδ. 根据参考文献[9,11]结论,在给定马赫数情况下,弹头对舵片升力的干扰系数只与展径比有关。对同一马赫数、不同攻角下的干扰系数进行对比,从而验证此结论。对马赫数为1.5和2.5,组件相位角γp不同,攻角α不同时的全弹进行数值计算,获得组件各舵片的修正力数据,并使用L-M算法对给定马赫数情况下、不同攻角的干扰系数进行辨识。
3.1 数值计算
由于风洞试验无法分离出单独导引组件的受力情况和单独舵片的受力情况,为了进行参数辨识,本文改为使用CFD方法计算所得数据。
根据气动工程模型中所需气动参数,可知数值计算使用模型分为带有导引组件的修正弹模型(见图4)和单独舵片模型(见图8)两种。前者用于求解舵片受力,后者用于求解舵片升力线斜率。与第1节相同,迭代计算中使用密度基求解器,对流项使用Roe通量差分格式离散,梯度使用最小二乘法求解,其他流动变量使用2阶迎风格式离散。使用S-A湍流模型使控制方程组封闭。流场入口边界使用压力远场条件,出口使用压力出口,双旋弹弹体表面使用无滑移壁面条件。计算条件如表1所示。
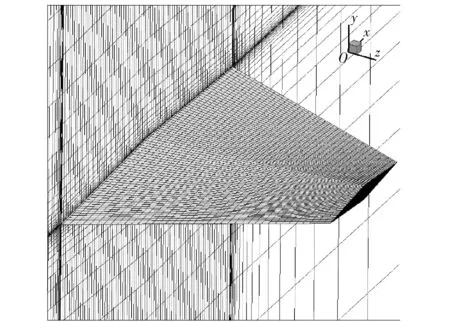
图8 单独舵片计算网格Fig.8 Grid of single canard
3.2 参数辨识
使用L-M算法对导引组件修正力气动模型中头部对舵片的干扰系数进行辨识。为了验证给定展径比情况下,干扰系数只与马赫数有关,与攻角无关,对马赫数分别为1.5、2.5,攻角分别为0°、2°、4°和8°时的干扰系数进行辨识。
L-M算法是非线性最小二乘法常用的一种算法,来源于对高斯牛顿法的改进。对于最小二乘问题:
(22)
式中:S(β)为残差平方和函数;β为待求参数向量;

表1 计算条件
方程f为所建立的模型;xi和yi是第i组已知的变量。
如同高斯牛顿法,方程f(xi,β+Δ)线性近似为
f(xi,β+Δ)≈f(xi,β)+JiΔ,
(23)
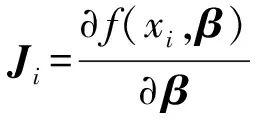
残差平方和函数S(β)在最小值时,S(β)对β的梯度等于0.
(24)
式中:N为样本个数。
对于多组已知变量,(24)式可以写成向量形式:
S(β+Δ)≈‖y-f(β)-JΔ‖2=
[y-f(β)-JΔ]T[y-f(β)-JΔ]=
[y-f(β)]T[y-f(β)]-
2[y-f(β)]TJΔ+ΔTJTJΔ,
(25)
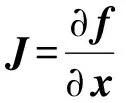
Δ=(JTJ)-1JT[y-f(β)].
(26)
(26)式给出了常规高斯牛顿法迭代增量的表达式。相比于高斯牛顿法,L-M算法引入了阻尼项入,L-M算法迭代增量如(27)式所示:
Δ=(JTJ+λI)-1JT[y-f(β)].
(27)
L-M算法优点在于可以调节:若残差下降太快,则使用较小的λ,使之更接近高斯牛顿法;若残差下降太慢,则使用较大的λ,使之更接近梯度下降法。
将本文建立的修正力工程模型写作矩阵形式:
(28)
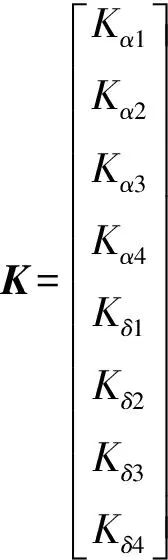
f(K)雅克比行列式为
(29)
通过多组迭代计算,对马赫数分别为1.5、2.5,攻角分别为0°、2°、4°和8°时的干扰系数进行辨识,得到的结果如表2、表3所示。计算表中每列数据的相对极差,结果如表4所示。在给定马赫数情况下,4片舵片的干扰系数随攻角相对变化均小于4.9%,因此可以验证文献[9,11]结论的正确性。
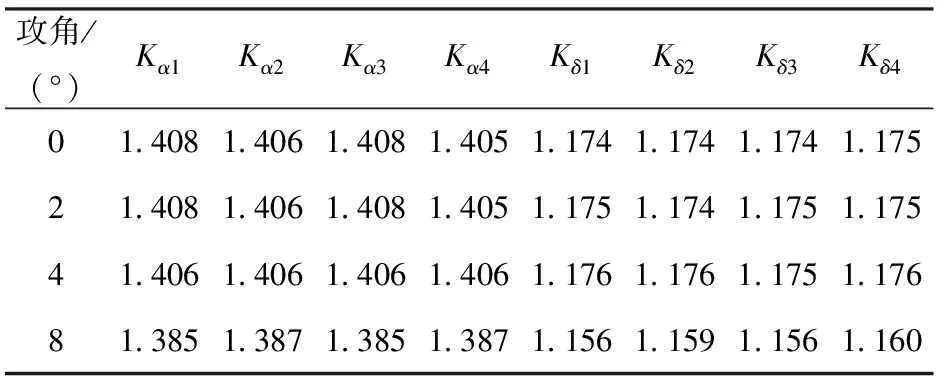
表3 马赫数2.5时干扰系数的计算结果
工程模型验证对比选取在马赫数分别是为1.5、2.5,攻角为4°情况下,分别使用文献[9]工程模型、本文工程模型进行修正力计算,与CFD计算所得结果进行对比,对比结果如图9所示。
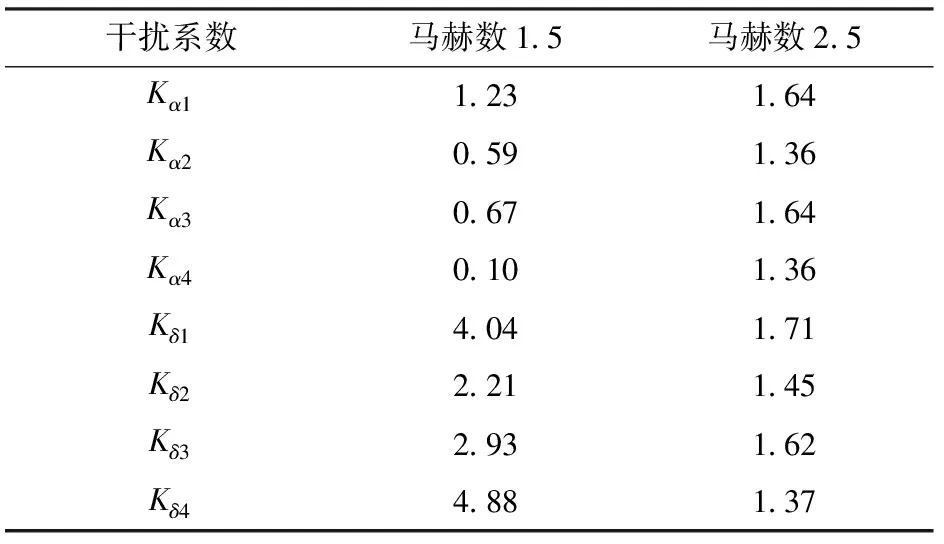
表4 相对极差
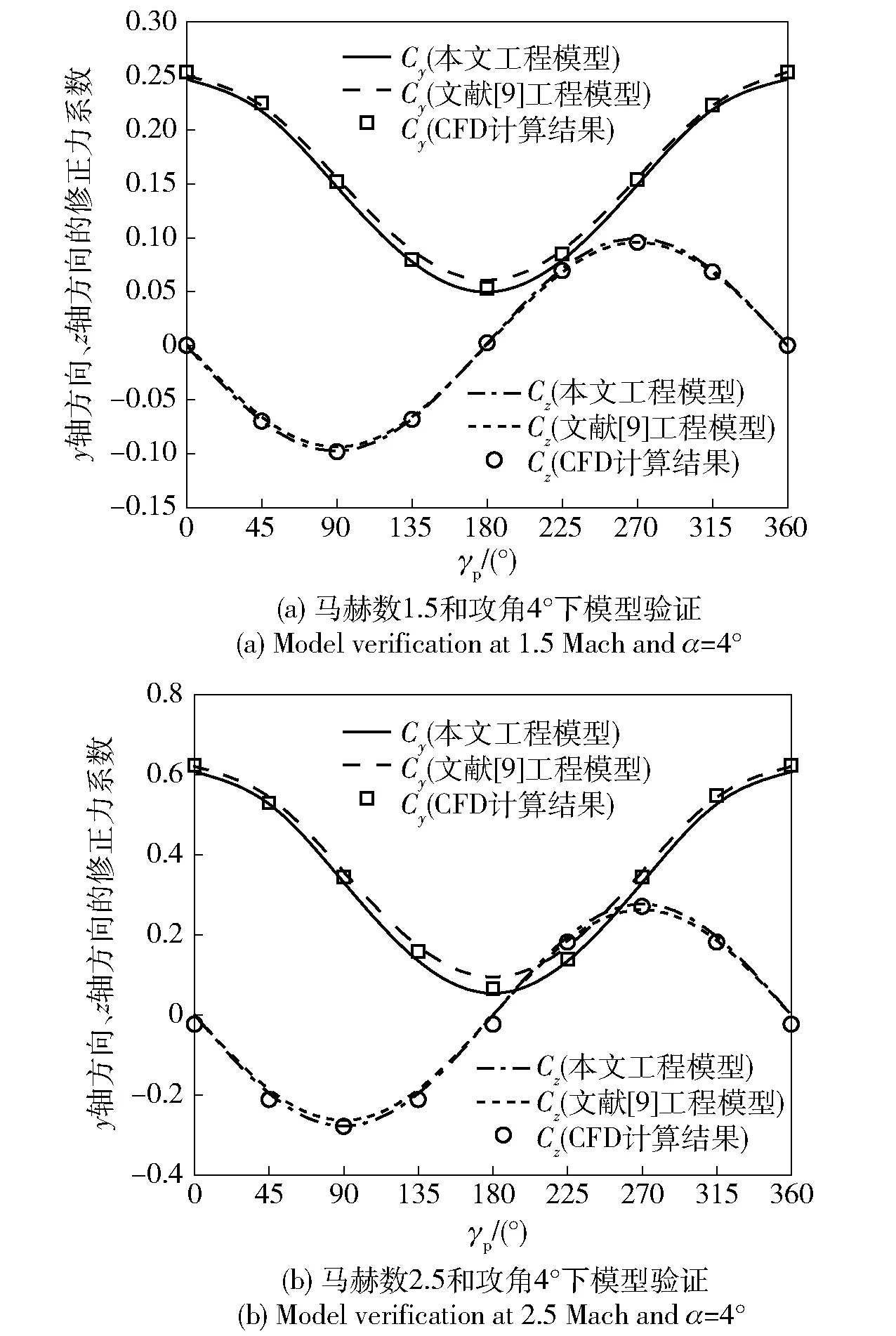
图9 CFD计算结果对工程模型的验证Fig.9 Validation of engineering model by CFD results
按照(30)式分别计算CFD计算结果与两种工程模型在y轴方向、z轴方向的修正力残差平方和SSR,结果如表5所示。
(30)
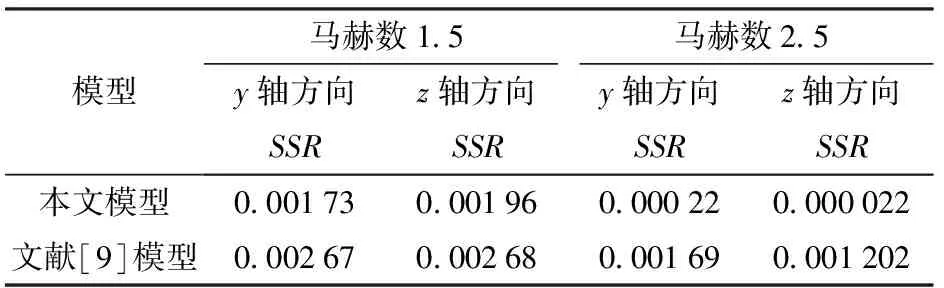
表5 残差平方和对比
通过对比两种模型的残差平方和,可知本文建立的工程模型残差平方和更小,因此可以认为本文建立的气动力模型更加符合物理规律。
4 结论
本文使用风洞试验数据对数值计算方法进行了验证,基于小扰动理论建立了基于4片舵片的修正力气动工程模型。依托数值计算结果,通过L-M算法对气动工程模型中的干扰系数进行辨识,并对模型进行了验证。根据以上研究得出如下结论:
1)阻力系数计算值与试验值的相对误差小于13%,升力系数计算值相对误差小于12%,数值计算方法有效。
2)本文提出的气动模型和文献[9]模型分别与数值计算结果进行验证拟合,结果(见表5)显示本文建立模型的残差平方和更小,因此可以认为本文建立的气动力模型更加符合物理规律。
3)在同一马赫数下,不同舵片干扰系数随攻角相对变化均小于4.9%,验证了给定马赫数下弹头对舵片的干扰系数对攻角变化不敏感。
本文改进后的修正力气动工程模型更加符合物理规律,头部修正组件的修正力模型与CFD计算结果吻合较好,对于修正弹的进一步飞行特性研究具有重要意义。
