小口径步枪弹头后效期运动特性试验与数值研究
2019-03-13陈川琳黄陈磊许辉李忠新吴志林
陈川琳, 黄陈磊, 许辉, 李忠新, 吴志林
(南京理工大学 机械工程学院, 江苏 南京 210094)
0 引言
膛口流场为包含强激波间断的高温、高压、高瞬态复杂非定常流场。发射药击发后,弹头在膛内火药燃气推动下,弹前空气柱受到弹头压缩,在膛口形成初始射流和初始激波;随后弹头底部离开膛口端面高温高压火药燃气因为脱离枪管的约束迅速膨胀,并进入初始流场,膛口周围出现各种复杂的物理和化学现象;弹头在火药燃气射流以及激波的相互作用下继续运动,膛口附近形成了复杂的非定常膛口流场波系结构。由于膛口流场的复杂性、高瞬态性,使得中间弹道学在弹道学中形成了独立体系,并且关于该部分的研究还在不断深化和补充。中间弹道过程的结果是枪外弹道的初始条件,因此对膛口流场与弹头作用的理解以及弹头在膛口流场中的运动规律研究,对提高武器射击精度等具有重要意义。
国外学者公布的关于膛口流场的试验主要应用电火花闪光照相技术,如Glass[1]利用阴影法获得了弹头初速马赫数为2的枪口时序阴影照片。Klingenbeg等[2]以脉冲激光为光源,测试出7.62 mm弹头膛口流场速度变化,并讨论了膨胀波和反应流之间的时序变化。随后,Klingenberg[3]采用时间积累的闪光照相技术观测了膛口初始流场变化过程,通过压电传感器测试压力波变化。Steward等[4]利用1 600 Hz高速相机对榴弹炮的膛口流场作用时间和作用范围进行了研究。另外,就大口径炮弹而言,有学者提出采用弹体安装压力传感器方法研究后效期阶段弹丸底部压力的变化[5-6]。国内对于膛口流场的试验也开展了丰富的研究,李鸿志等[7]应用闪光照相技术对多种口径常规武器的膛口流场进行了可视化试验,获得了丰富的试验照片。郭则庆等[8]应用直接阴影法对7.62 mm口径弹道枪的膛口流场开展了可视化试验研究,着重分析了不同膛口装置下流场特征。王宝元等[9]对火炮后效期时间和作用距离测试提出了基于高速摄影的可视化试验方法,并测试了某小口径炮弹靶场射击时的后效期时间和作用距离。通过分析上述文献可知,大量的试验研究,特别是枪弹膛口流场试验研究都采用闪光照相的可视化方法,但该方法每次闪光在膛口处获得照片数量极为有限,一般时序照片是通过多发枪弹在击发后不同时刻曝光获得的。然而,考虑到弹头对于膛口流场变化影响比较小,闪光照相的可视化方法在研究膛口流场变化仍具有重要意义[8]。为了排除不同枪弹间差异对弹头在膛口流场中运动的影响,更好地研究弹头在膛口流场中的运动规律,本文提出了一种基于高速摄影的阴影照相法来获得同一发弹头运动的连续图像。
数值方法也是膛口流场研究中的重要手段。Jiang等[10]基于任意Lagrange-Euler(ALE)方程及动网格技术对44 mm口径弹丸由内弹道时期的膛内运动直至飞离初始流场的全过程进行了数值分析,并讨论了激波的反射以及激波对弹丸加速的作用。代淑兰等[11]采用三维非定常化学反应流控制方程组对带制退器7.62 mm口径、初速为735 m/s的弹头膛口燃气流场燃烧过程进行了数值分析,清晰地描述了膛口流场发展过程、流场结构和性质及弹头与流场的相互影响。郭则庆等[12-13]基于ALE方程有限体积方法,利用AUSM+格式和分区结构化贴体网格重点研究了初始流场对膛口流场变化的影响,并开展了弹头后效期运动研究。郁伟等[14-16]、Zhang等[17]和Yu[18]基于耦合内弹道过程的膛口流场仿真手段,针对不同武器对象开展了膛口流场分析。Qin等[19]通过基于耦合内弹道的膛口流场数值方法结合组分标记的手段,重点研究初始流场对膛口流场燃烧规律的影响。周鹏等[20]对高压气体装置的膛口流场进行了数值分析,获得弹丸运动特性曲线和膛口流场变化规律。其中,弹丸在火药燃气作用下运动数值研究中,初始流场对膛口流场发展的影响是不能忽略的[12],因此弹头在膛内运动的加速规律需要合理设置。然而,公开可查阅的膛口流场数值研究文献中鲜有以试验数据作为膛内运动边界参数控制依据的报道。为合理设置膛内运动,本文以膛压试验数据为膛内运动边界的设定准则,采用耦合内弹道的膛口流场数值方法开展后效期弹头运动和受力规律的研究。
1 试验研究
研究弹头在膛口流场运动规律过程中,观测同一发枪弹弹头在膛口流场中连续变化,不仅直观而且能排除闪光照相法中因不同枪弹特性差异带来的误差影响。这种连续的运动变化观测结果与数值计算结果对比和验证更具有合理性。
1.1 试验方案
本文采用间接阴影照相方法对膛口流场进行可视化试验。阴影照相法是一种较为实用的可压缩流场可视化方法,其基本原理为光线经过密度不均匀流场时会发生偏转,从而在成像平面上形成光照强度不同的像[8]。此外,本次试验同步测试了弹壳口部的压力。为了描述弹头膛内运动特性,测压试验采用电测法获得试验条件明确的时序膛压曲线,可为更深入理解初始流场的形成和发展机理提供参考,同时为数值计算提供运动边界。
1.2 试验系统搭建
图1所示为可视化试验系统示意图。可视化试验系统主要由高速摄影、采集卡控制箱、电荷放大器、高照度LED光源、压电传感器等组成。拍摄弹头在膛口流场运动全过程,当枪弹击发,弹头在膛内运动,经过测压孔后,压力传感器接收脉冲信号,控制箱中的同步器同时触发测压采集模块和高速摄影采集模块。在高照度LED光源作用下,弹头运动、膛口流场时序变化将清晰可辨地由高速摄影捕捉,膛压时序变化曲线也在试验系统测压模块中采集。

图1 可视化试验系统示意图Fig.1 Schematic diagram of experimental system

图2 试验场景Fig.2 Experimental setup for data capturing
如图2所示试验室为封闭暗室,排除外界杂光和风的影响,室温23.7 ℃,相对湿度65%~70%,具体拍摄参数如表1所示。

表1 试验拍摄参数
1.3 试验结果和分析
试验不仅拍摄到弹头连续运动过程,同时也清晰记录了膛口流场的变化过程。如图3所示为高速摄影捕捉某发5.8 mm口径步枪弹膛口流场变化影像。图3(a)中,弹头在膛内加速,弹前空气柱受到压缩并在膛口形成初始射流,该部分无色透明,呈现含入射激波、反射激波、马赫盘、射流边界湍流气团等构成的激波瓶结构。图3(b)中,弹尖运动至枪口端面,此时少量泄露的火药燃气离开枪膛束缚,迅速补充初始流场并把激波瓶向下游推进,到达图3(c)时,弹头底部刚好到达枪口端面,随着弹头运动,膛口与弹头间隙增大,泄露的火药燃气量增多,极大补充初始流场,激波瓶明显变大,冲击波强度变强。火药燃气中有未燃尽的火药晶体,因此影像中火药燃气部分呈深色。图3(d)~图3(f)记录了弹头出膛口后的火药燃气和初始流场相互作用的过程。图3(d)为弹头出膛口后,膛内高压火药燃气突然释放,在弹头和膛口端面区立即形成火药燃气激波,火药燃气激波在侧向上呈球形波膨胀。此时,火药燃气射流速度大于弹头速度,受弹头尾锥部影响形成弹头底部激波。火药燃气射流受到相交激波和弹头底部激波影响,火药燃气经过马赫盘压缩升压并在弹尖区域汇聚形成一个高密度压力突跃层,使燃气激波冲破球面波约束,火药燃气激波和初始射流界面的轴向运动速度大于侧向运动速度,波阵面向下游突出。图3(e)时刻弹头底部激波限制了火药燃气射流强马赫盘的形成,在火药燃气射流继续补充和推动下,高密度压力突跃层不断增厚和加速,因为轴向速度远高于不断衰减的火药燃气冲击波波阵面速度,于是,受火药燃气激波的束缚,火药燃气高密度气团逐步演变为凸出在弹头前方的高压气团,呈冠状气团。图3(f)所示冠状气团向径向膨胀,其轴向突跃面不断追赶下游的火药燃气激波,压力间断面强度不断增加,逐步叠加形成冠状激波的雏型[21]。由图3(g)可见,随轴向位移增加,火药射流轴向波阵面运动速度减小,最终和弹尾端脱离,由于火药燃气核心区气体为亚音速气流,弹头底部激波消失,在射流区域形成马赫盘。弹头继续运动于图3(h)时刻穿越火药燃气冲击波,此时膛口流场对弹头作用消失,时间为0.211 ms(对应第82598帧),弹头底部距离枪管口部187.46 mm. 由此可见,试验中所采集数据清晰丰富,可以完整呈现膛口流场变化和弹头运动,从一定程度上说明了所设计的试验方法和试验参数在小口径枪弹膛口流场研究中具有一定适用性。

图3 某发5.8 mm口径步枪弹发射过程时序影像Fig.3 Shadowgraphs of eight sequential muzzle flow fields of a 5.8 mm bullet
2 数值计算
试验研究中获得了5.8 mm口径步枪弹弹头膛口运动和膛口流场的连续变化图像,以及弹壳口部同步的膛压变化。正如引言所述,针对国内鲜有文献公开对弹头膛口运动计算结果与试验数据进行验证和结合的研究,同时,考虑到膛内运动的合理性将影响初始流场分布特性,本文采用试验和数值计算相结合方法,将试验获得的膛压数据为数值计算提供膛内运动过程的运动边界,该部分将写成用户自定义函数(UDF),采用4阶5级龙格- 库塔法协同FLUENT16.0计算。所提供的初始流场分布和膛内气压分布将作为膛口流场计算的初始条件和边界。最后用试验数据验证数值计算结果的可靠性,同时数值计算也为弹头运动研究提供更为丰富的数据。
2.1 数学模型
膛口流场数值模拟中作如下假设:
1)膛口火药燃气形成的射流服从轴对称流动规律,对称轴为枪管轴线;
2)将火药气体与外界空气看成同一介质,忽略火药燃气多组分化学反应的影响,状态方程服从完全气体状态方程[22-23]。
2.1.1 控制方程
不考虑外加热和彻体力的影响,笛卡尔坐标系下二维轴对称可压缩非定常Navier-Stokes方程为
(1)
式中:Q为守恒变矢量,
ρ为气体密度,vx和vy别为x轴和y轴方向的速度分量,E为总能量,
pa为气体压力,γ为气体比热比;f和g分别为x轴和y轴方向的通量;S为轴对称源项。

式中:qx、qy分别为x轴方向、y轴方向单位质量的体积加热率;τxx、τyy、τxy、τθθ分别为x轴方向、y轴方向、Oxy平面切向、圆周方向上的黏性力,
μ为层流黏性系数。
由理想气体状态方程得出压力表达式为
(2)
2.1.2 湍流模型
计算采用的湍流模型为Realizablek-ε模型,与标准k-ε模型相比主要有两个不同点:1) Realizablek-ε湍流模型为湍流黏性增加了一个公式;2) Realizablek-ε模型为耗散率增加了新的传输方程。引入Boussinesq线性涡黏假设,雷诺应力表达式[24]为
(3)

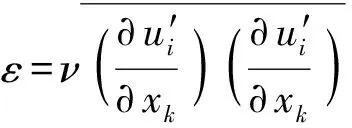

2.1.3 动网格与离散格式
为了处理计算过程中弹头运动引起的网格变化,需要采用动网格技术。依据数值计算中的假设1,采用铺层法。铺层法包含了边界上网格的生成和消失,会根据计算区域的扩张或收缩来生成或合并(消除)相应的网格[22]。模型采用2阶精度AUSM+离散格式,AUSM+格式将流动对流特征中的线性场和非线性场相区别,并将通量分裂为对流项和压力项分别处理。AUSM+格式具有间断分辨率高、数值耗散小以及稳定性好等特点[23]。
2.1.4 网格划分和边界条件
本文主要研究弹头在膛口流场中的运动,气动外形对弹头在膛口流场中运动影响不可忽略,其外形参数如图4所示。

图4 弹头外形Fig.4 Configuration of a 5.8 mm bullet

图5 膛口流场的物理模型示意图Fig.5 Physical model of muzzle flow field
对具有复杂外形的流场进行模拟时,很多情况下很难生成单块高质量结构网格,此时可以采用分区混合网格的方法进行处理。枪管总长460 mm,管壁厚6.96 mm,定义为wall边界。如图5所示,周围流场区域长600 mm、宽420 mm,定义为压力出口边界。最小网格尺寸为0.05 mm,为避免非结构网格带来过多的计算量与格式耗散,本文采用的混合网格共17.4万个。为验证本文所采用的网格划分方法及网格尺寸、数量的合理性,以总网格数20.6万的计算模型作对比,两种情况后效期弹头底部压力最大误差不超过1%,证明所划分的网格能保证结论可靠。
2.2 膛内运动模型
本文数值仿真计算中,弹头膛内运动速度,即弹头膛内运动边界是由经典内弹道提供的。某型5.8 mm口径步枪弹使用球扁药,根据几何燃烧定律,同时考虑燃烧过程仅有减面燃烧阶段,该枪弹的内弹道由5个方程组成。
1)形状函数:
ψ=χZ(1+ξZ+ηZ2),
(4)
式中:ψ为火药燃气相对生成量;Z为相对已燃厚度;χ、ξ、η为发射药的形状特征量。
2)燃烧规律:
(5)
式中:e1为发射药半弧厚;u1为燃速系数,u1=1.86×10-8;p为膛内平均压力;n为燃速指数,n=0.86.
3)动量方程:
(6)
式中:φ为次要功系数;m为弹头质量;v为弹头速度;S为枪管截面积。
4)能量方程:
(7)
(8)
式中:l为枪管长度;lψ为药室自由容积缩径长;f和ω分别为火药力和装药量;ζ=γ-1;Δ为装填密度;V0为药室容积;l0为药室容积缩径长;ρp为火药密度。
5)运动方程:
(9)
在编写UDF和FLUENT耦合计算时,为避免因各参量数量级悬殊而导致计算截断误差过大,需要将上述方程进行归一化[25]。
引入相对变量:

最终归一化后的方程为
(10)
式中:
2.3 模型计算结果
2.3.1 弹头膛内运动边界设定
UDF中的内弹道程序将实时为数值计算提供弹头运动边界和弹后空间压力边界。弹头运动规律影响初始流场的形成,弹后空间压力分布对弹头出膛后燃气冲击波的形成和演变至为关键。
如图6所示,从压电传感器获得的弹壳口部压力变化看:测试膛压曲线在0.293 ms时,达到最大膛压值289.01 MPa;弹头出膛口时刻,试验测试值为68.09 MPa. 由于没有点传火过程,弹壳口部测压孔测试压力不是从大气压开始逐渐升高,而是约在击发后0.03 ms开始逐渐升高。当弹头运动经过测压孔,高压火药燃气突然加载,传感器受高压冲击载荷作用,测试曲线产生阶跃响应。根据试验数据进行符合计算,由UDF计算内弹道膛压,最大平均膛压为285.070 MPa,对应时刻为0.280 ms. 弹头圆弧部恰好完全离开枪口端面时刻,通过UDF计算获得的膛口压力为66.451 MPa.
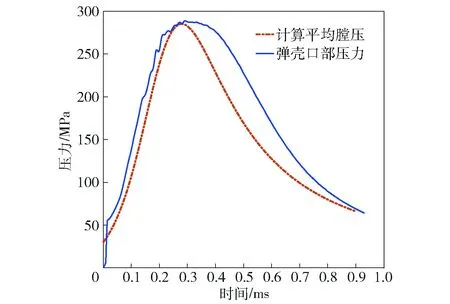
图6 弹壳口部测试压力与计算平均膛压 Fig.6 Pressure vs. time
由UDF计算弹头在膛内运动曲线如图7所示。从图7可以看出,弹头圆弧部和圆柱部交接处恰好完全离开枪口端面时刻,此时速度为882.702 5 m/s.
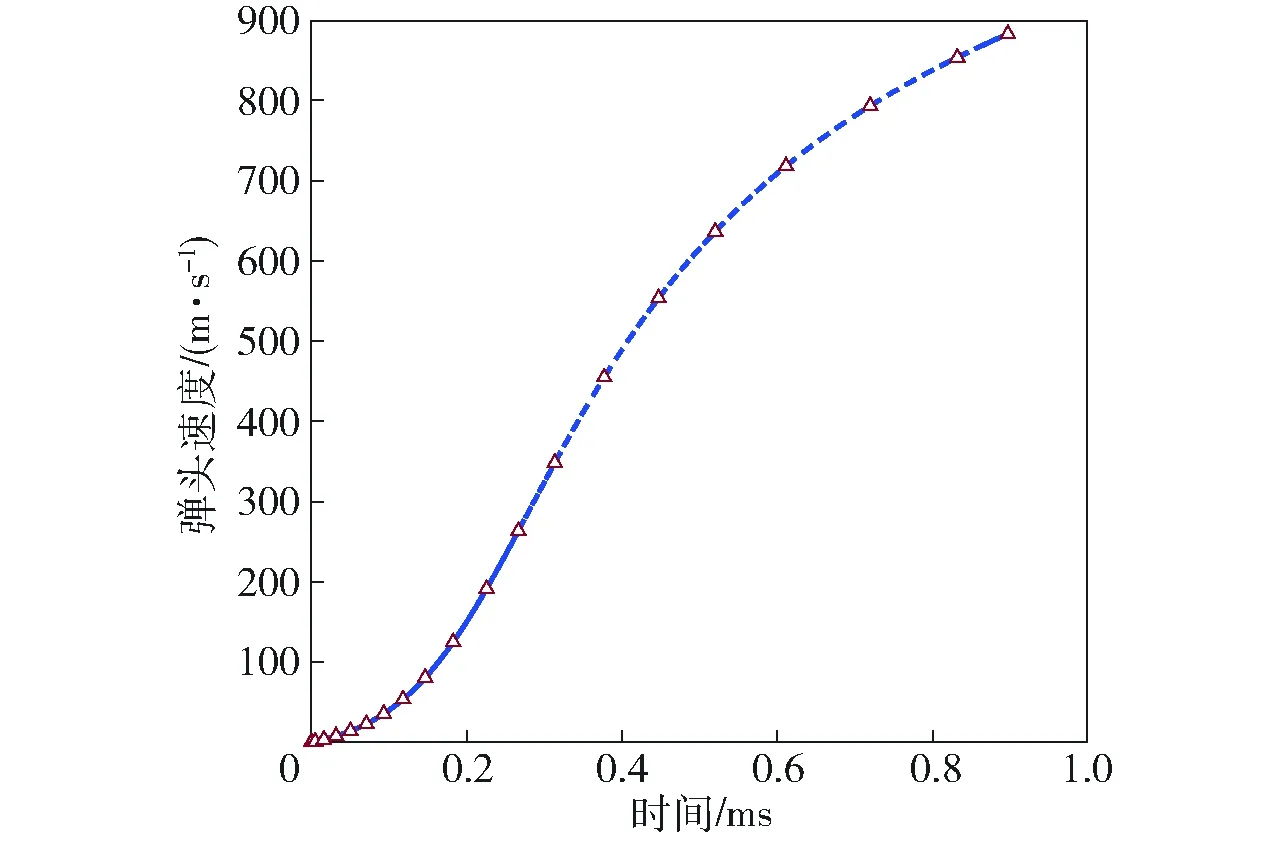
图7 弹头在内弹道时期的速度曲线Fig.7 Velocity vs. time during the interior ballistics
2.3.2 数值计算结果分析
图8所示为初始流场的仿真结果与试验结果对比。由图8可以看出,初始流场主要因弹头膛内运动压缩产生弹头前部的空气,如此弱激波瓶结构在数值计算中仍被精细捕捉到,进一步证明了膛内运动规律有其一定的合理性,也说明了所使用方法对于弱激波有较好的分辨能力。图9所示为弹头出膛口后火药燃气激波分布情况。由图9中仿真结果可见,即将与火药燃气冲击波闭合时刻,冠状气团在弹体头部汇聚,火药燃气射流速度大于弹头速度,在弹头底部产生弹底激波。由图9中试验结果可见,冠状气团在弹尖汇聚,弹底激波及其连接处的激波位置、最外围火药燃气激波、火药燃气射流的核心区域轮廓和数值方法计算获得的阴影图几乎一致。通过强、弱激波的计算阴影图和试验观测图对比,说明所用数值方法和计算参数可以较好反映实际流场的变化情况,可以为弹头运动研究提供更丰富的数据支撑。

图8 初始流场阴影图(下)与仿真结果(上)对比Fig.8 Numerically calculated (upper) and experimental (below) precursor flow fields around muzzle

图9 第82587帧火药燃气阴影图(下)与仿真结果(上)对比Fig.9 Numerically calculated (upper) and experimental (below) muzzle flow fields at the 82587th frame

图10 不同时刻的弹头底部轴向位移Fig.10 Axial displacement vs. time
与1.3节试验结果分析一致,本文定义第82579帧为0 ms时刻,此时弹头底部恰好和枪口端面平齐。图10所示给出了弹头底部距离枪口端面的轴向位移- 时间曲线。其中,误差棒为多次判读的误差,最大标准偏差为2.47 mm. 弹头行程180.45 mm,各时刻计算流体力学(CFD)计算数据均对比试验数据均值,其最大偏差为4.35 mm,可见基于试验膛压数据的耦合内弹道膛口流场CFD方法计算研究5.8 mm口径步枪弹轴向运动具有一定的可靠性。
3 弹头膛口受力和运动分析
2.3节已经验证了数值方法的适用性,本节基于仿真计算结果对弹头膛口运动和受力进行分析。
文献[13]对弹头外形进行了简化、没有考虑尾锥部,研究轴向合力时仅考虑了弹头和弹尾部的压力差,而实际上尾锥部也是弹头的重要组成部分,本文研究将对完整的弹形进行计算。为了更精确地研究弹头受力情况,不再沿用文献[13]提出的用弹头底部与头部压力差作为轴向力,改为采用实时压力场在沿弹体表面积分获得的弹头轴向合力。与文献[13]另外不同的是,采用的数值模型考虑了初始流场的影响。
如图11所示,给出了以弹头底部恰好离开枪管为0时刻,弹头在膛口流场中运动的速度变化和轴向合力分布。由图11可知:时间t=-0.015 ms时,弹头弧形部和圆柱部连接处恰好与枪口端面平齐,此时弹头进入半约束期;弹头底部受到火药燃气作用,t为-0.015 0~0 ms时,弹头轴向合力约保持在1 346.77 N,弹头速度由882.702 5 m/s增加到888.229 m/s;随着半约束期结束,t为0~0.062 9 ms时,火药燃气脱离了枪管束缚,高温、高压燃气迅速向四周膨胀,弹头底部压力大幅减小,弹前阻力增大;t=0.062 9 ms时,火药燃气对弹头轴向合力减小为0 N,弹头达到的最大速度为890.42 m/s;膛外加速期结束,进入膛外减速期,火药燃气推力继续减小,弹头持续减速,直至t=0.211 ms时,弹头底部完全离开火药燃气激波,后效期结束,弹头进入外弹道阶段自由飞行。

图11 弹头在膛口流场中运动速度和轴向压力Fig.11 Velocity-time and axial force-time curves
预估弹头后效期运动,工程上常假设弹头底部压力由出膛瞬间弹头底部压力峰值于后效期作用时间内指数式衰减为0 N,即F=Ae-Bt,假设0~0.211 ms之间,轴向压力由峰值1 346.765 4 N衰减趋于0 N,易得A=1 346.765 4 N,B=107 819,即得图11所示的经验轴向压力。
忽略弹前阻力的影响,弹头在弹头底部压力作用下的速度变化可表示为
(11)
式中:弹头初速v0=888.229 m/s;弹头质量m=4.55 g. 经验轴向压力作用下的速度曲线如图11所示。经验模型计算弹头在0~0.211 ms之间,速度由888.229 m/s增加至890.97 m/s. 通过CFD方法计算,最大速度为890.42 m/s,可见通过CFD计算方法计算的弹头运动特性具有一定的可信度。
综上所述,表2所示总结了弹头分别在半约束期、膛外加速期、膛外减速期的速度变化Δv,速度变化占速度最大变化Δvmax的比例Δv/Δvmax,以及各过程所占时间比例Δt/Δta. 其中:弹头在膛口流场中运动的速度最大变化Δvmax=vmax-vmin;Δta为半约束期、膛外加速期、膛外减速期3个阶段的时间之和。

表2 弹头膛口运动参数对比
如表2所示:半约束期所占作用时间最短,对速度变化影响却最为明显;与之相反,膛外减速期虽作用时间约占整个膛口运动时间的60%以上,但对速度影响几乎可以忽略不计,这一结论也同时说明了忽略减速期的工程方法可以较精确地描述弹头膛口速度变化的原因。
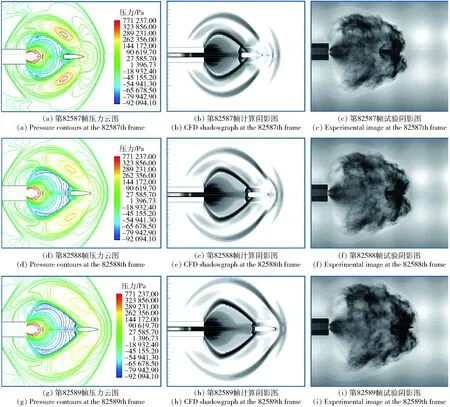
图12 轴向压力转变前、后一帧的压力云图、计算阴影图、试验图对比Fig.12 Pressure contours, numerically calculated shadowgraphs and experimental images of muzzle flow fields at different times

图13 不同时刻的弹头表面压力分布Fig.13 Pressure distributions of a 5.8 mm bullet at different frames
为了说明轴向压力转变点产生的机理。图12所示分别展示了在轴向合力为0 N时刻前、后一帧的情况,即t为0.053 05~0.072 75 ms时刻的压力云图、计算阴影图、试验图的对比。从图12(b)可以看出,此刻弹头速度较低,阻碍了火药燃气射流轴向膨胀形成弹底激波,弹头向前移动,弹底激波减弱,波阵面逐步向上游弯曲,同时冠状气团不断压缩,在图12(e)时刻形成冠状激波。从图12(h)可以看出,随着弹底激波减弱,由于火药燃气经过马赫盘后变为亚音速,弹头穿越马赫盘后,弹底激波完全消失。在上述图12(b)、图12(e)、图12(h)变化过程中,弹头附近流场最明显的变化有两个方面:一方面弹底激波强度减弱,由图12(a)、图12(d)、图12(g)可见;另一方面,由于冠状激波的形成,弹前气流密度增加,静压力增加,如图12(b)、图12(e)、图12(h)所示,如图13所示弹体表面4~23 mm区域的压力变化也说明了这一点。图12(e)、图12(f)、图12(i)的流场变化也显示了和数值计算相同的规律,弹底激波减小直至消失,同时弹前的冠状气团逐渐形成冠状激波。通过轴向合力转变过程的物理现象试验研究和数值分析可知,该5.8 mm口径步枪弹在后效期运动过程中,存在膛外加速期和膛外减速期两个阶段。轴向合力转变点在弹头完全穿过马赫盘形成之前,此时弹头底部仍存在弹底激波。有别于7.62 mm口径步枪弹膛外减速开始于弹底激波消失的结论[13],5.8 mm口径步枪弹膛外减速期开始时刻仍然受到火药燃气核心射流的作用,即弹底激波依然存在。在加速期末期,随着弹头运动,弹底激波作用减小,火药燃气推动力迅速减小,同时,冠状气团密度、压力不断增大,最终形成冠状激波,弹前阻力增大,最终弹头进入减速期。
4 结论
为了研究小口径枪弹在后效期的运动和受力规律,本文提出了一种基于高速摄影结合阴影照相的方法,并开展了相关试验研究。应用耦合内弹道的CFD计算方法对弹头运动和受力规律进行了分析。所得结论如下:
1)本文高速摄影结合阴影法在研究小口径步弹头的后效期运动试验研究中,可获得清晰的膛口流场变化和弹头运动过程影像。
2)基于耦合内弹道的CFD计算方法,阐明了弹头在膛口流场中运动的3个阶段:半约束期、膛外加速期和膛外减速期。给出了各阶段的时间、轴向力和运动速度的变化。
3)在膛外加速期和减速期的转变点研究发现:对于某型5.8 mm口径步枪弹,两个时期的转变时刻弹头受到火药燃气核心射流和弹前冠状气团的组合作用。在加速期末期随弹头运动,火药燃气推动力迅速减小,同时冠状气团密度、压力不断增大,弹前阻力增大,最终弹头进入减速期。
与膛外加速期和膛外减速期的转变时机和机理相关结论,将在后续工作中进一步深化,并设计相关试验进行验证。
致谢南京理工大学机械工程学院蔡红明副教授对本文数值计算部分提出宝贵建议;南京理工大学机械工程学院蒋明飞博士在试验实施过程中给予的帮助。
