“圆”满解题:例谈辅助圆求最值

安徽省安庆市第二中学 (246001) 王 庆

最值问题是高中数学中重要的内容，常常与其它知识点一起考查，可以从多个角度思考，能用多种方法解决.它能够全方位考查学生解题能力和数学思想，因此最值问题是高考的重点和热点.由于最值题型较多，因此根据试题选择解题方法是这类问题的难点.数形结合思想是高中数学中最重要的数学思想之一，数形结合法往往能让抽象问题直观形象化，让复杂问题简单化.下面介绍利用数形结合思想构造圆来处理最值的方法.

一、外接圆解单动点问题

最值问题中一定含有动点(变量)，若只有一个动点(变量)时，常常构造外接圆解决问题.

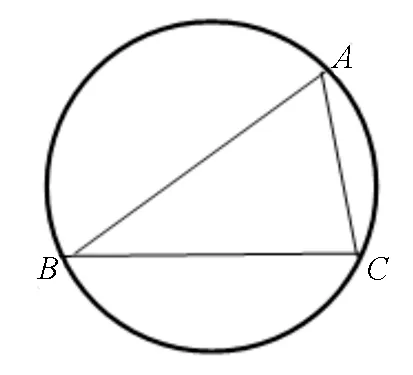
图1

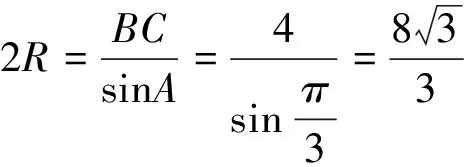
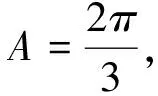
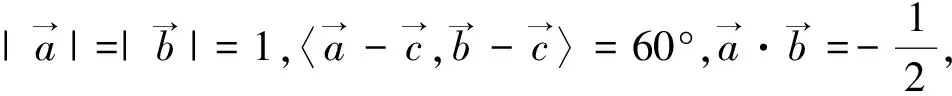
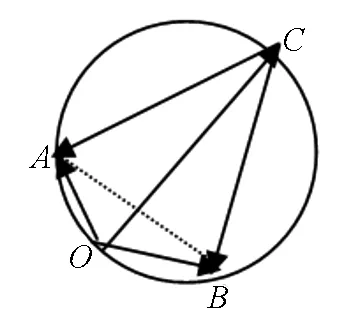
图2

二、组合圆解多动点问题

最值问题中含有多个动点(变量)，常常需要构造多个圆，利用动点(变量)间关系处理问题.

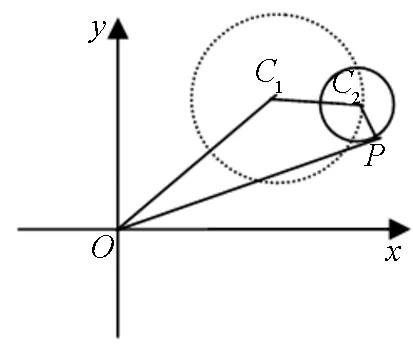
图3

例3 已知实数x，y满足(x-2cosθ-3)2+(y-2sinθ-4)2=1，θ∈R.求x2+y2取值范围.

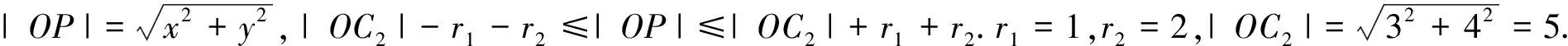
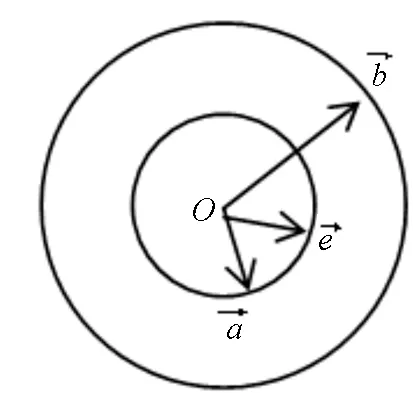
图4

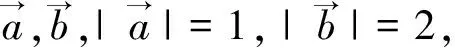
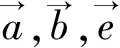
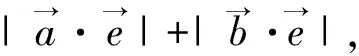
解决最值问题时，常常选择数形结合法，以形导数，以形助数，既直观形象，又减少了计算量，同时还体现了直观想象的数学核心素养.圆具有对称性，图形简单等特点，作为考查数形结合思想的载体方便易行，并且事半功倍.