微专题“扬帆”，学习进阶“导航”*

江苏省宜兴市丁蜀高级中学 (214221) 邵 曦

学习进阶理念在数学学科的研究主要有两个方面：第一类是理论性的基础研究，通过实证方法建立纵向的学习进阶；第二类是将学习进阶应用于数学课程、教学和评价中的研究.学习进阶理念是对学生学习路径的研究，探索学生思维如何发展.

一、学习进阶的概念和特点

学习进阶(Learning Progression)的理念最初由美国国家研究委员会提出，为了促进美国学生更好的掌握核心概念，打破传统教学模式[1].近年来，该理念被引入到各种学科的教学当中，但是数学领域的研究仍然处于起步阶段.

学习进阶从提出到现在，仍然没有一个统一的定义，来自全世界的多个学者都提出了自己的看法，例如Songer、Salinas、Duncan等.进行归纳后可以发现提出的定义主要有四类：过程论、假设论、方法论和序列论.目前被广泛接受的是认为学生的学习过程是发生在一个大的时间间隔内的，学生在这个时间内不断的学习完善自己的知识体系，更加深入的对知识进行研究，整个过程中学生需要经历多个不同层次的中间水平.首先，学习进阶是基于核心概念展开的，数学中的核心概念可以是抽象的模型思想，也可以是倍数、统计量等具体知识点，学习进阶的整个过程需要围绕核心概念不断深入；其次，进阶的途径不是固定的，是可以改变的.对于不同的学生，学生进阶的途径是不一样的；最后，学习进阶具有假设性和层级性，学习进阶是循序渐进的，通过不断验证假设修改完善最初的学习进阶方案.

二、微专题教学的概念

微专题教学指的是在数学教学过程中，围绕着某个知识点或者数学思想开展研究，从知识或者思想初始的概念开始，不断渐进，并且通过一条清晰的主线串接起来的教学过程.微专题具有灵活、实用和有效的特点，能够让不同层次的学生在整个教学活动中起到作用，并且提升综合能力[2].

三、学习进阶在高中数学微专题教学中的应用

学习进阶由五个要素组成：进阶起点和终点、进阶水平、学业表现、进阶维度和测评工具.教师首先需要选取一个范围合适的核心概念，随后查阅文献资料，了解核心概念.下面将以苏教版高中数学“函数零点”这一核心概念为例，建立函数零点高三复习微专题，阐述“学习进阶”在高中数学微专题中的建立.

1、确定进阶起点和进阶终点

学习进阶的起点指的是学生已经具备的知识技能和学习经验，进阶的终点指的是学生最终需要达到的目标，也就是学生可以达到的最高水平.教师首先需要对本班学生已有的知识储备有一定的了解，随后查阅资料文献，结合课程标准、教学目标确定进阶的终点.

例如在“函数零点”的学习进阶建立中，进阶起点的设计如下：进阶起点1：学生在前面学习中已经熟练掌握了解方程的方法，例如因式分解法、配方法和公式求解法.进阶起点2：学生已经熟练掌握各类基本函数图像，能够理解和应用函数图像与坐标轴之间的关系，以及依据判别式判断函数图像与x轴的交点个数.进阶终点是：学生能够结合函数图像以及基本函数的性质，使用分类讨论的数学思想解决复杂的零点问题，让学生深入理解体会零点问题的精髓，可以灵活的将不等式问题转换成为零点问题.

2、建构精准性学习进阶

在实际的教学过程中，教师根据班级的实际情况修改假设性学习进阶，设计符合本班学生实际情况的分层进阶学习方案.数学教学是基于练习来完成的，学生通过不断的练习，来掌握和学习知识.教师依据进阶起点，结合学生实际的情况，在假设进阶的基础之上，选取代表性题型，引导学生进行思维的迁移和发散，促进学生形成完整的逻辑链，体会其中的数学思想，从而达到进阶终点.

例如在零点问题的教学设计中，在学习进阶理念的指导之下，可以从设计如下三个层级的学习内容，促进学生逐步加深理解.

层级1：直接应用，基础层级

对于零点问题，其进阶的起点是理解“显性”零点，结合方程的思想和函数图像，找到解决零点问题时的转换方法：函数的零点⟺方程的根⟺函数图像与横坐标轴的交点.学生若想从进阶的起点进阶至下一个层级，需要完成一定的练习，同时教师通过讲解例题和习题的过程中，引导学生总结规律，从而学生可以高质量的完成层级跨越.

例1 (1)求函数f(x)=x2+x-6的零点;

(2)判断f(x)=x2+2x+4的零点个数.

解析：(1)全部学生都可以将零点问题转换成为方程问题，随后解方程x2+x-6=0，超过半数的学生使用了因式分解的方法进行解答(x+3)(x-2)=0，可以得到x1=-3,x2=2.剩下的学生采用了判别式法进行解答.

(2)此题中学生们采用了判别式Δ<0和函数图像两种方法得到了零点个数为0.

设计意图：例1的设计目的是为了让学生通过自己动手练习，可以体会到方程、函数图像和零点之间的关系，同时巩固之前所学习的方程求解方法.

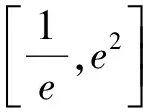
解析：例2在前面例题的基础上添加了区间，同时函数变得较复杂，学生若不能进行适当的变形，则无法正确解答此题.

求解f(x)=x-lnx-2的零点，即求x-lnx-2=0的解的个数，依靠学生现在的水平，是没有办法直接进行求解的，但是上式可以变为lnx=x-2.此时可以通过分别画出y=lnx和y=x-2的图像，通过在区间内交点的个数进行判断.

设计意图：此题是“隐性”的零点问题，这类零点问题往往不能通过方程思想进行求解，需要依靠图像，结合数形结合的思想解决问题.学生通过解答此类问题，可以得到此类问题的一般解法，从而提升思维.

通过以上两个例题可以发现，层级一是在进阶起点上的直接应用，主要就是“解”，就是要求学生使用所学的知识，解决问题.这一层级的学习主要是通过模仿练习，不断的巩固知识，总结规律.学生若处于这一层级，教师需要多加以引导，帮助学生找到知识盲区，进入下一层级.

层级二：变形应用，能力层级

在零点问题的基础题之上加入参数，是对零点问题的变形，参数的位置改变等都会使得问题变得不一样，使得零点静态问题变为动态的.引入参数之后，零点问题开始变得复杂起来，需要使用分离参数的方法和函数单调性的判断，这样使得学生的思维从形式表征到方法思想讨论的多维度进阶.

例3 请讨论以下问题(1)求当k取何值时，f(x)=x-lnx-2-k有两个零点；(2)f(x)=kx-lnx-2有且仅有一个零点，求k的取值范围；(3)若函数f(x)=x-klnx有两个零点，请求出此时k的取值范围.

解析：(1)在此问中，将参数引入到了常数项的位置，结合函数图像引导学生思考，这只是将函数进行上下平移，因此可以直接根据图像得到：当k>-1时，函数有两个零点.第二种方法是使用分离参数的方法，讨论y=x-2-k和y=lnx的交点个数，在例2的图像基础上进行平移就可以得到相同结论.

(3)此时将参数k的位置移动到了lnx前面，使得问题变得更加复杂，但是整体的思路仍然相同，可以结合图像得到k的取值范围为(e,+∞).

此层级的例题相比于基础层级，在思维和解题复杂程度上都有了明显的提升，需要学生在掌握好基础知识规律的同时，能够认真分析题目，结合分离参数方法进行解答.

层次三：综合应用，发散层级

进阶终点是学生的综合应用能力，学生在掌握了零点的定义、判定定理等概念之后，需要结合分类讨论、数形结合等数学思想，解决复杂的数学问题.因此学习路径中的最后一个层级，是在前面两个层级的基础之上，逐渐递进，达到较高的水平.

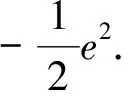
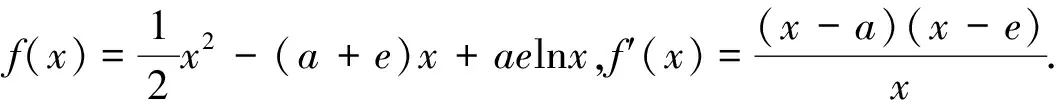
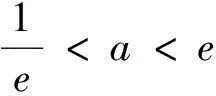
第三层级也就是最高层级，是学生在高中阶段需要最终达到的层级.通过前面两个层级的铺垫，学生整合了相关的知识要点和思想方法，最终达到综合应用层级.

在本节“函数零点”的教学设计中，是基于进阶分层理论为学生设计的学习路径，借助习题按照“直接应用、变形应用、综合应用”三个层级设置具体的内容[3].教师在具体的实施过程中，会及时观察学生的学习情况，即判断学生处于哪一个层级，若学生处于第一层级，则加以引导，找出学生的问题所在，帮助学生快速进入到第二层级当中；若学生处于第二层级，要引导学生找出瓶颈所在，从而达到最终层级.

总而言之，“学习进阶”理念指导下的高中数学教学，既需要教师根据学生现有的知识水平、学习能力，结合层级水平，确定不同层级学生的学习方向；又要不断的调查了解学生的层级水平，了解学生已经学到了多少知识，理解了多少知识，可以应用多少知识解决问题，从这些方面判定学生的层级，帮助学生从进阶起点不断努力，跨越连续层级，抵达进阶终点.