数学文化如何在高中课堂教学中生根发芽*

江苏省吴县中学 (215151) 张 芳

新的课程标准已经将数学文化作为一个独立的要求融入课程内容中，要求把数学的文化价值渗透到课程内容中.通过数学文化的学习，学生应该需要初步了解数学科学与人类社会发展之间的相互作用，体会数学的科学价值、思维价值、应用价值、人文价值，开阔视野，寻求数学进步的历史轨迹，激发对于数学创新原动力的认识，学生如果能够长期的受到优秀的数学文化熏陶，领会数学的美学价值，那么自身的文化素养和创新意识也会得到进一步的提升，核心素养和“四基”也能够慢慢的养成.这和我们现阶段的新课程标准所要培养的学生正是相辅相成、不谋而合的.

数学文化不但包含了数学家，数学史，数学美，数学教育，也包括了数学的思想，精神，方法，观点，语言，以及他们形成和发展所包含的领域，其不仅仅是在课堂上，更多的是与我们的生活息息相关，所以教师在课堂教学中其实还可以从多方位，多角度的渗透数学文化，而不是在课堂开始或者结束的地方轻描淡写地嫁接一些数学名人名句或者数学史，这样的生拉硬套难免就失去了课标中设置数学文化的初衷.数学文化不能单独成一章节，应该在必修、选修课程中都应得到体现.

那么如何更好的渗透数学文化的课堂教学呢？笔者认为可以从以下几方面做好文化渗透的教学，不当之处还请各位专家批评指正.

一、让学生从数学史中发现数学的有趣性

数学家M·克莱因曾说：“数学史是数学教学的核心.”由此可见，只有充分的了解了数学的发展史，才能更好的学好数学的知识技能.而现阶段，学生往往会有如下一些误区：“高考对数学史没有要求，在高考的压力下，学习数学史有点浪费时间”、“学习数学史无形中增加了我们学习的负担，我们连最基本的知识都没有弄清楚，学习数学史又有何用”.这些想法其实已经偏离了设置数学史的“初衷”.了解数学史并不会增加学习的负担，相反了解了数学史的发展反而会更加增进对数学知识的理解与掌握.而了解数学史也能在数学解题中得到更好的应用.提升数学史的关注度，提高教材中的数学史知识呈现的有效性.通过图表文字结合的方式增强学生的学习趣味性；善于组织数学史教材，将数学史渗透到日常的教学中来，使数学文化的知识贯穿于课堂.

兴趣是最好的老师，兴趣是探索研究的起源，学习数学首要的任务就是要培养学生学习的兴趣，有了这个“兴趣”老师就不怕学生学习数学时感到枯燥无味了.众所周知，数学史中有很多丰富多彩且生动有趣的小故事，这些故事既贴近生活又富含哲理，让学生了解这些故事既能带动学生学习的积极性、主动性，又能使他们形成良好的数学的情感态度价值观.

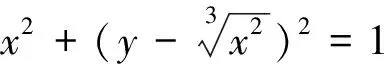
二、让学生从练习中发现数学文化的重要性

数学文化的内容往往并未直接在教材中给出，是蕴涵于数学知识之中，是从数学内容反映出来的.因此教师要把显性知识中所隐含的隐性的数学文化及时挖掘出来，并呈现给学生，让学生不仅掌握了数学知识，而且还了解了数学史，达到了数学知识与数学发展史有机的统一，相辅相成.

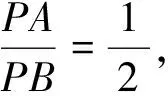
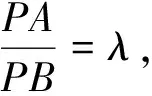
三、研究高考试卷中的数学文化的典型题

近些年,以名题为背景的高考试题,在一些省份的试卷中多有出现,也深受广大教师和学生的喜爱.其次也体现出对新的课程标准中文化目标落实起着导向性的作用.

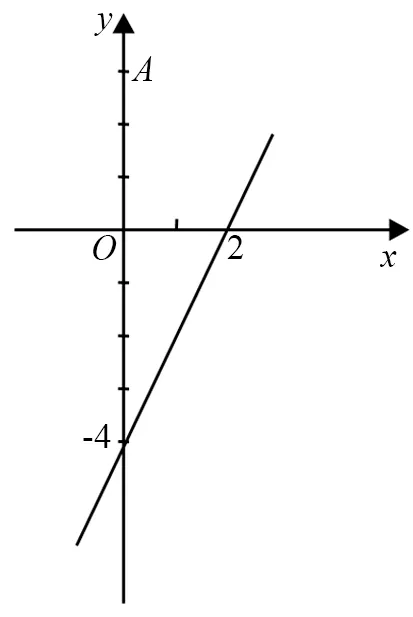
图1

(2)如图1，在平面直角坐标系xOy中，点A(0,3)，直线l：y=2x-4.设圆的半径为1，圆心在l上.

①若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；②若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

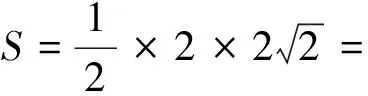
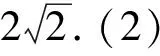
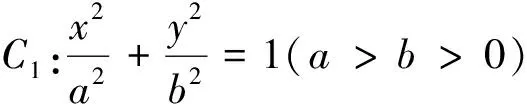
(1)求椭圆C1的方程；

(2)若动点P(x0,y0)为椭圆外一点，且点P到椭圆的两条切线相互垂直，求点P的轨迹方程.

此题是2014年广东高考理科卷的第二十题，其中第二小问是我们解析几何中另一个“大名鼎鼎”的圆—蒙日圆.创新并不是无中生有，空穴来风，要有坚实的基础.以数学名题为背景的试题不断出现，对教师和学生都提出了新的挑战和机遇.尽管试题的设计来源于世界数学名题，但处理问题的手段和方法还都没有逾越中学阶段所应该掌握的、具备的能力，基于此,作为教师自身就应该了解试题的来龙去脉，要懂得数学名题的经典处理方法,才会把数学文化更好的渗透到学生的思维水平中.作为新时代的人民教师,传播弘扬数学文化是我们义不容辞的责任,但也要清楚地认识到,数学文化的传播肯定不是一朝一夕就能完成的，而是要在潜移默化中让学生慢慢加以接受.数学教学也应该越来越多地考虑到数学文化的渗透，有计划、有目的和自然地引入到数学教学中，让数学文化帮助学生学习数学、理解数学、深刻地认识数学和真正地去应用数学，让数学真正发挥它应有的作用.

四、让学生从网络资源寻求数学的创新性

在数学文化目标真正落实的过程中，很多一线教师受到了时间的约束，教学进度的影响，往往在教学中感到十分的困惑，不知道如何进行数学文化教学的渗透，更受迫于高考升学率的压力，轻视了数学文化的渗透，通常是例行公事，敷衍检查，若是公开课，教师则可能生拉硬套地简单贴加一块数学史，或是简单讲讲数学历史上的人物和相应的事迹，讲讲数学家的生平，以及数学概念、公式、定理等成就诞生的历史背景．以为这就是进行了数学文化的教育了.而若没人听课，那么上课则就又回到了原来传统的样子.其实教师学生如果以这样的心态来理解要学习数学文化的话，那就大错特错了.随着高考自主命题省份不断增加，越来越多的大学教授和数学专家参与高考命题.大学教授们非常希望通过此类试题的考查来选拔一些有发展潜能的人才.这种类型的试题落脚点一般是：著名的数学问题、著名定理、著名公式或著名图形等，如高考试题除了上面我们提到的阿波罗尼斯圆、蒙日圆等著名的数学文化背景以外，还出现过以杨辉三角、四色问题、蝴蝶定理、哥尼斯堡七桥问题、克拉茨猜想等等为背景的试题，这种试题观点较高，试题的知识点源于初等数学的内容，解题的手段和方法一般也是中学中较常用的.以名题为背景的试题使得这些考试对中学数学教学的创新和改革以及对数学文化的渗透起到明显的导向作用，更能够调动中学数学教师积极地在课堂里渗透数学文化，拉近课标理念与实际教学的距离.通过高考试题文化背景的渗透,学生对数学文化的理解又会达到一个新的理性的高度.

其实现在已经进入了互联网家的时代，学生的学习不能再是老一套的方法，更多的可以借助网络媒体这样的工具，教师也可以适当给出相应的数学文化学习的任务，布置一些课外阅读，让学生在课余兴趣活动中多了解数学的发展历史.特别是高一的学生刚进入高中，学习的压力没有那么大，学校或备课组完全可以专门开设数学课外选修课，让学生可以借助于课外选修课的机会，老师与学生一起学习数学史，也可以通过网络媒体一起了解学习相应的数学发展史.

最后引入叶中豪先生一句话，“数学是一种文化，而文化就是要被继承的东西”.教师本身也需要加强数学文化的学习，提高自身数学文化素养水平，数学教学应将“让数学变得文化些，还数学以文化之本来面目”作为每个数学教师追求的目标.我们要从学生的终身发展出发，多思考如何将数学文化在我们的课堂上生根发芽，从而让课堂教学绽放绚丽的光彩.