抛物线内接三角形的面积
2019-03-08山东省莱芜市教学研究室271100房增军
中学数学研究(江西) 2019年2期
山东省莱芜市教学研究室 (271100) 房增军
对于坐标系内某一个具体的三角形的面积,我们有很多方法可以求得,但对于无法确定形状的三角形,其面积求法很难统一起来.经过推导,抛物线内接三角形的面积满足统一的表达式,现分享给大家,有不正确的地方,请指正.
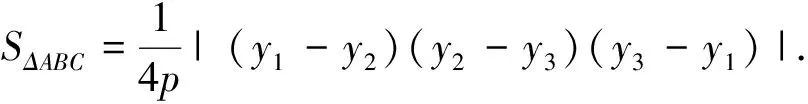
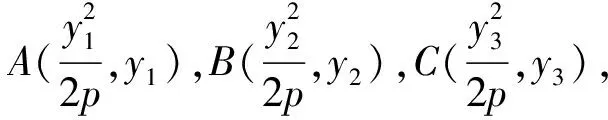

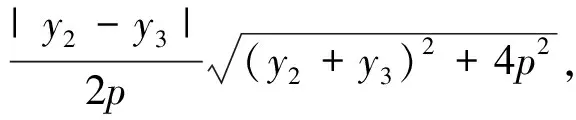
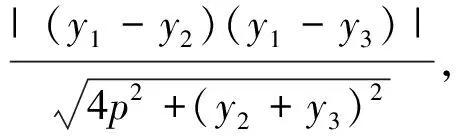
注:如果A、B、C三点中有两点关于x轴对称,易知上述公式也成立.
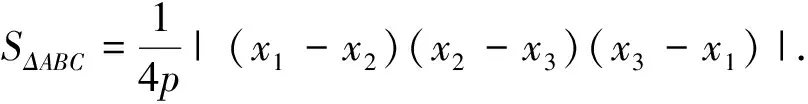
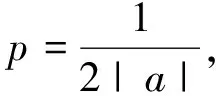
对于抛物线的内接三角形的面积,还有一个重要的结论.
已知A、B、C是抛物线y2=2px(p>0)上三点,过A、B、C三点的抛物线的切线分别交于P、Q、R三点,则SΔABC=2SΔPQR.
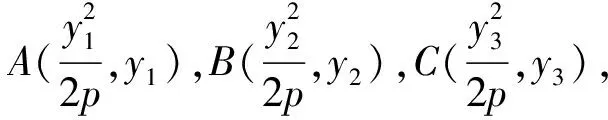
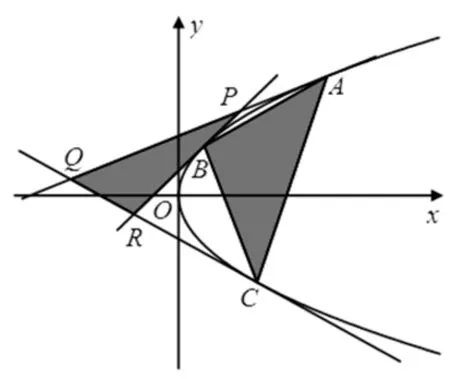
图1
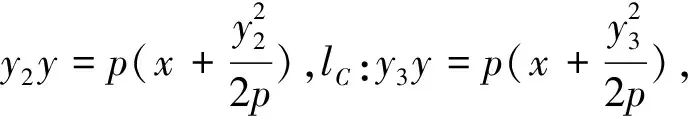
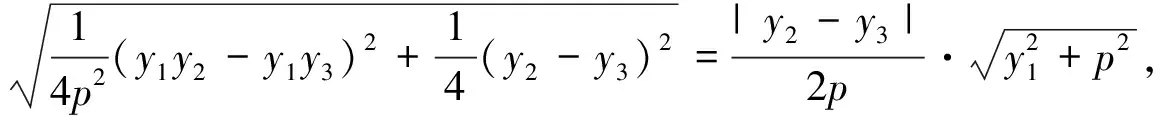
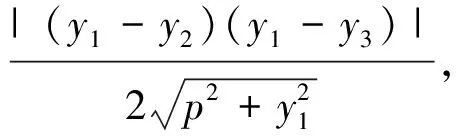
注:如果A、B、C三点中有一点与原点重合,易知上述公式也成立.
∴根据前面的公式,可得SΔABC=2SΔPQR.
在圆锥曲线中,抛物线具有重要地位,它有很多很重要的性质.抛物线方程结构简单、代数计算量适中,并且关于抛物线的试题具有良好的区分度.结合初中学过的二次函数,对于进一步理解抛物线很有帮助,研究抛物线的相关性质,掌握这些性质对于其它圆锥曲线的学习有很好的借鉴意义.
