素养导向下的2018年高考数学试题选析

广东省增城中学 (511300) 邱昌燕

一、试题回顾

(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB.

全国卷Ⅰ文科20.设抛物线C:y2=2x，点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点．

(1)当l与x轴垂直时，求直线BM的方程；

(2)证明：∠ABM=∠ABN.

二、试题分析

这两道题是2018年全国卷Ⅰ理科和文科的解析几何解答题，第二问都是证明角相等，两角相等本属平面几何范畴，但用初中平面几何难以求证，必须把角化归为斜率之和为零采用代数的方法求证，故两道题都体现了高中解析几何的精髓，也即考查了解析法.理科第19题以椭圆为载体，文科第20题以抛物线为载体，然这两道题的第二问有本质的关联吗?

三、本质探究

为探究问题的本质，用字母代替数字，且把问题设置成存在性问题进行探究.

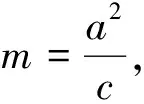
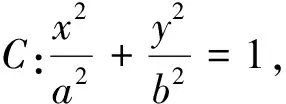
把③④代入⑤化简得mp=a2.此结论对于双曲线会是怎样情况呢？

解：对于双曲线的运算只须把椭圆中的b2改成-b2，仍得出结论：mp=a2.探究到此，对于圆的将要探究的结论则显而易见了.

探究4 设圆C：x2+y2=a2，过圆C内部点P(p,0)的直线l与C交于A,B两点，问是否在x轴上存在点M(m,0)?使得∠OMA=∠OMB,O为坐标原点.

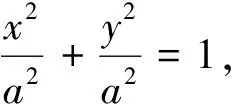
探究5 设抛物线C:y2=2px，过抛物线C内部点T(t,0)的直线l与C交于A,B两点，问是否在x轴上存在点M(m,0)，使得∠OMA=∠OMB，O为坐标原点.

解：假设存在点M(m,0),使得∠OMA=

把①②代入③得m+t=0,即m=-t.

综合探究1至探究5可得四个结论：

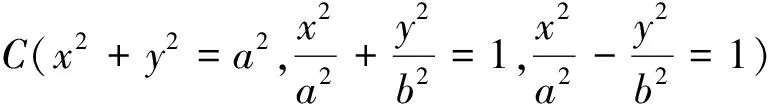
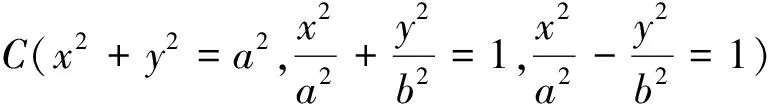
结论3 过抛物线C:y2=2px内部点T(t,0)的直线l与C交于A,B两点,则存在唯一点M(m,0)(m=-t),使得kMA+kMB=0.

结论4 过抛物线C:y2=2px外一点M(m,0)分别作两斜率互为相反数的直线交曲线于A,B,D,E,则等腰梯形ABDE任一对角线必过定点T(t,0)(t=-m).

四、功能评价

任子朝先生在《从能力立意到素养导向》一文中指出：“素养导向不但强调知识和智力,更强调知识的迁移和后天的习得.考查目的在于更清晰、准确地考查学生的智力水平、思考深度、思维习惯和科学态度.素养导向的高考命题重视学科观念、规律的考查，将这些学科知识作为素养养成和发展的基础和先决条件.素养导向高考命题注重科学思维的考查，科学思维是对客观的事物本质的属性以及潜在的规律和相互之间的关系的一种认知方式.素养导向的高考命题更注重科学探究能力的考查.素养导向的高考命题更注重情境化试题的考查，情境活动包括生活实践活动与学术探究情境活动[1].”而本文选用这两道高考试题设计的五个探究符合从能力立意向素养导向命题的转变，对提升学生的数学素养有一定的功效，具体表现在下面几个方面：

首先，用字母代替数字化的探究运算，对运算要求比较高，对提升学生的运算素养很有帮助，只有注意力高度集中，具有强烈运算意识和运算品质才尽可能避免运算出错.其次，上述探究活动本身就是一个学术知识探究情境活动，故有助于培养学生科学的探究素养.再次，上述探究活动的设计有助于培养学生深度化思考的习惯和激发学生兴趣，苏霍姆林斯基说：接近和深挖事物的本质及其因果联系的实质.这一过程本身就是兴趣的主要源泉.最后，经过深度思考探究后这一类型问题有本质的认识后也即提升了学生素养,对探究试题后的优美结论:mt=a2(有心曲线)和m+t=0(抛物线)了解和掌握可帮助学生快速解决同类型的试题，如：

(1)求点G的轨迹C的方程；

(2)过点T(4,0)作斜率不为0的直线l与(1)中的轨迹C交于A,B两点，点A关于x轴的对称点为D，连接BD交x轴于点Q，求△ABQ面积的最大值．

2018年全国高中数学联赛陕西赛区预赛试题：如图，圆C与x轴相切于点T(2,0)与y轴的正半轴相交于A,B两点(A在B的上方).且|AB|=3.

(1)求圆C的方程；

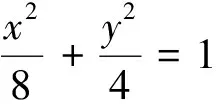
学生会解答问题是能力问题，学生能看清问题的本质从而能快速解答就是素养问题，显然素养考查比能力考查要求更高，更强调平时深度的思考及后天的习得.