几道高考压轴题的自然解法与解题思考

福建省闽清教师进修学校 (350800) 黄如炎

导数与函数综合题大多作为高考压轴题，主要考查理性思维和创新意识.对导数与函数综合题学生思路迷茫，一筹莫展，在考试中几乎是空白题.高考命题组给出的标准解答具有抽象、严谨、精练、规范的特点，体现了数学的理性思维，很有数学味，但由于没有给出解题的思维过程(连图形都没有)，使人很难领悟标准解答，对直接给出的某些结论，学生感到莫名其妙，如坠烟海，不利于学生思维的培养和素养的发展．

“数学是自然的，数学是清楚的”[1]，因此数学解题应是清晰明理的！本文对2018年高考几道典型的函数与导数压轴题，探析不同于命题组标准解答的自然、明快的解法，从中感悟解决函数与导数综合问题的基本通径和主要对策．

1 试题探析

题1 (2018年高考全国Ⅲ卷理科第21题)已知函数f(x)=(2+x+ax2)ln(1+x)-2x．(1)若a=0，证明：当-10时，f(x)>0；(2)若x=0为f(x)的极大值点，求a．

第(1)步略，第(2)步探析如下．

探析:f′(x)=(1+2ax)ln(1+x)+

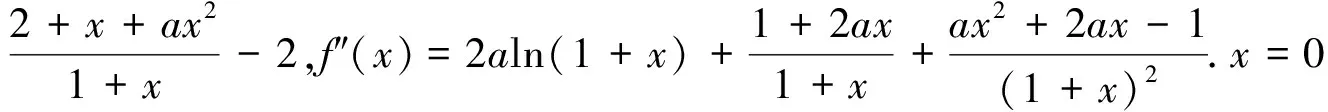
图1

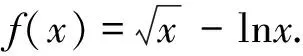
第(Ⅰ)步略，第(Ⅱ)步解析如下．

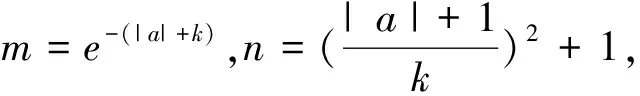
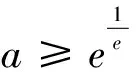
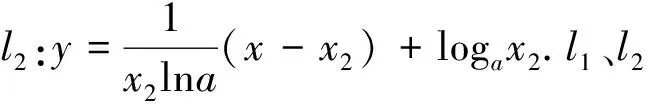
标解评析:命题组的标解是通过研究函数u′(x)的零点、单调性和符号，找到函数u(x)最大值u(x0)，再证u(x0)≥0，还用到第(Ⅰ)步的结论．本解法不用探求u(x)最大值，无需前问铺垫，通过特殊点的精准验证和函数式的灵活放缩，达到优化解题思维，提高解题品质．

题4 (2018年高考全国Ⅱ卷理科第21题) 已知函数f(x)=ex-ax2.

(1)若a=1，证明：当x≥0时，f(x)≥1；

(2)若f(x)在(0，+∞)只有一个零点，求a．

第(1)略，第(2)步解析如下．

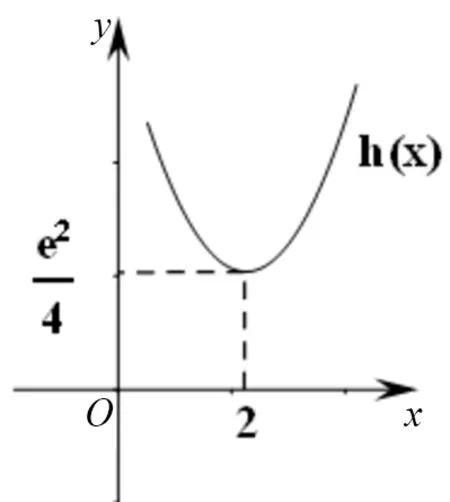
图2

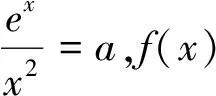
标解评析:命题组的标解是根据f(x)=ex-ax2=e2(1-ax2e-x)，把f(x)在(0，+∞)只有一个零点等价转化为h(x)=1-ax2e-x在(0，+∞)只有一个零点．在寻找h(x)零点存在区间时，利用不等式ex>x2进行放缩，较难想到．

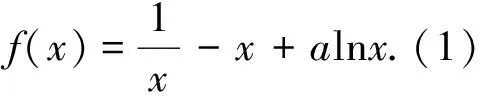
第(1)步略，第(2)步探析如下.

2.解题思考

《普通高中数学课程标准》(2017年版)指出：“直观想象是发现和提出问题、分析和解决问题的重要手段，是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础”[2].函数图像刻画了函数的性质，图像为抽象的推理增添了形象支持，在茫然的思路中，图像指引着推理的方向．因此研究函数与导数综合问题要顺应学生从形象思维到抽象思维的认知过程，通过直观想象，把对“形”的感知转化为对“数”的表达．求解函数与导数综合问题的基本通径为：

(1)求导，确定函数单调区间．

(2)作图，根据函数单调性和关键点(如定义域区间端点、坐标轴交点、极值点等)作出函数图像．

(3)推证，依托图像确定推理证明的方向．

函数与导数综合题常涉及到零点存在问题，导函数零点不可求问题，不等式问题和含参问题，主要解决对策有：

(1)对函数零点存在问题，关键在零点两侧探求实数m、n(可以是一个具体的数、式或区间)，使f(n)f(m)<0．

①特值验证：根据函数式的特征，取特殊自变量m，验证是否满足f(m)>0(或f(m)<0)．

②解不等式：当不等式f(x)>0(或f(x)<0)可解时，可直接通过解不等式求出满足f(m)>0(或f(m)<0)的实数m．

③放缩化归：当f(x)较复杂时，可将f(x)放缩为简单的函数g(x)，使f(x)>g(x)(或f(x)0(或g(m)<0)，则f(m)>g(m)>0(或f(m)

为便于放缩，可根据函数图像和解析式特征，在某特定范围内进行放缩．对含有指、对数函数的要注意运用重要不等式ex≥x+1,lnx≤x-1进行放缩．还要注意能否利用前问结论进行放缩．

(2)对导函数零点不可求问题，可再次求导，通过高一阶导函数的零点研究函数性质．若多次求导后的函数零点仍不可求，可将函数放缩或化归转化为简单的函数求解．

(3)对不等式问题，要先构建相应函数再运用导数求解(证)．

(4)对含参问题，要注意变量分离和分类讨论的缘由．

教学中要讲道理，多体悟，力求解题思路的自然形成.教师要启迪学生利用直观想象与推理论证相结合的方法，沿着求导→作图→推证的基本路径，通过特值验证或放缩化归探求函数零点存在区间；通过再次求导或放缩化归解决导函数零点不可求问题；通过构建函数和求导求证(解)不等式；通过分类讨论或变量分离求解含参问题．