一类不等式的简证

新疆生产建设兵团第二中学 (830002) 张国治 江睿煊 张益斌 李 响新疆乌鲁木齐市第68中学 (830001) 何雨辰

面对庞杂的知识体系和大量的模拟试题，如何针对高考竞赛展开高效的针对性复习？通过对近几年高考和竞赛试题的研究，笔者有一个很有趣的发现——试题各异，出题角度多变，但探源溯流，它们来源于同一个问题．我们可以把这类不断衍生的题目称为“题根”．那么如何寻找“题根”呢？将源于课本的题目进行提炼与升华形成结论，然后再将其广泛应用于解题实践中，这便是寻觅“题根”的不二法门了.这一过程意义非凡，因为茫茫题海中很多题目表面不同，但实质一样(可归结于同一个“题根”)．一个“题根”加工而成的结论，其功效不亚于教材中的一个定理.笔者从一个重要的不等式出发，探源溯流得到竞赛题、高考题命题的题根，并给出一种高效学习数学的方法，敬请同行指正.[1]

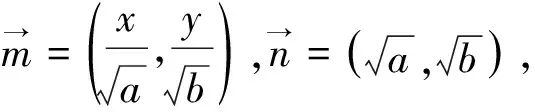
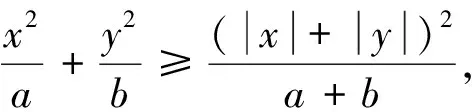
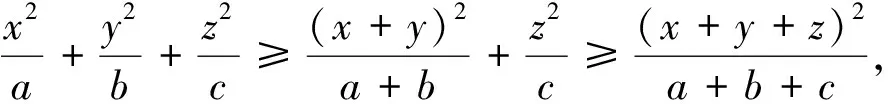
下面以近期竞赛试题和数学通讯问题征解为例谈谈此不等式的应用，追本溯源，以期抛砖引玉，凸显回归题根的重要性.

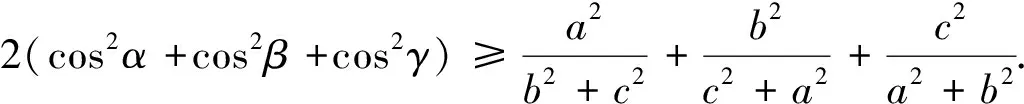
分析1：解决三角形中的问题，通常是采用“减元”的策略，即将“边元”和“角元”做一转化.考虑到待证的不等式是分式结构，可以利用本文结论和正弦定理便有如下简洁明快的证法.

证明1：根据正弦定理，右边等价于

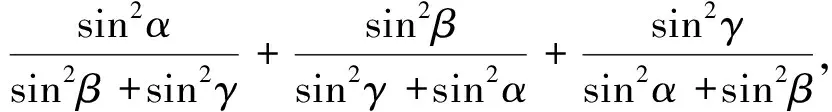
分析2：由题设结构联想到射影定理：在ΔABC中，有a=bcosC+ccosB,b=ccosA+acosC,c=acosB+bcosA成立.由本文结论推广便有如下别具一格的证明.

点评：上述证明过程中巧妙的用到了射影定理和本文引理的推广，由证明过程不难得到下面推广：

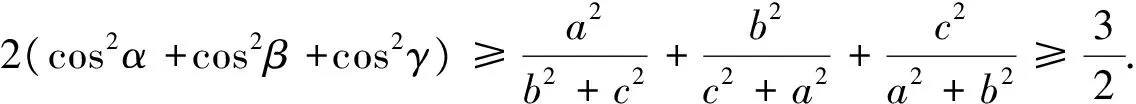
分析：本题几个作者提供标准解答是先利用比较法证明2(a4+b4)≥(a+b)(a3+b3)2.然后利用基本不等式获解，解法显得很突兀，非常不自然且不易推广.但倘若利用本文的结论便有如下简洁明快的解答.

按上述证明不难作如下推广：

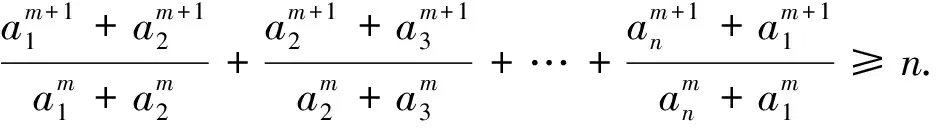
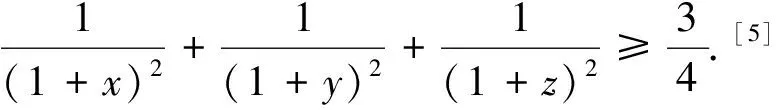
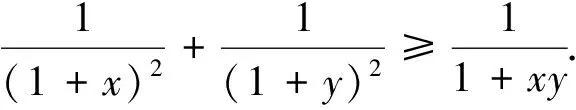
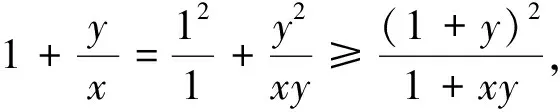
按上述证明不难作如下推广：

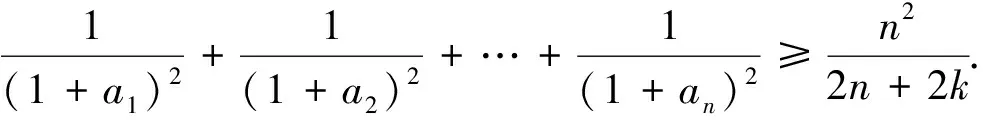
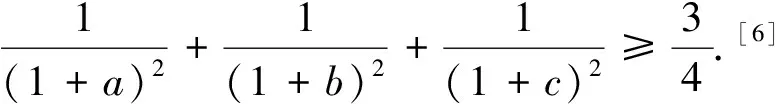
按上述证明不难作如下推广：

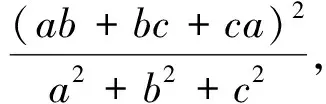
分析：本题标准解答利用柯西不等式获解，但倘若利用本文的结论便有如下别具一格的解答.

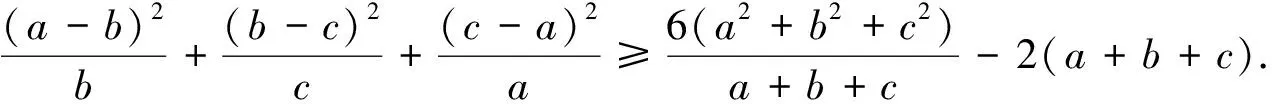
按上述证明不难作如下推广：

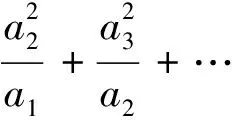
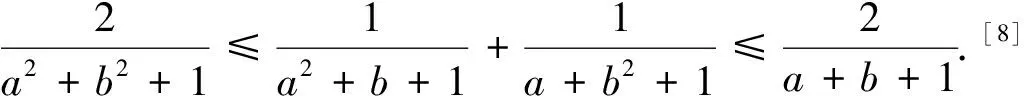
分析：本题标准解答利用柯西不等式获解，但倘若利用本文的结论便有如下别具一格的解答.

按上述证明不难作如下推广：

总之，研究“题根”对教学、命题和解题都有深远的意义，变幻多端的数学题目犹如葱郁繁密的树叶.看似难以捉摸，实则息息相关，故而在研究问题时应拨开层层枝叶，寻其根源，以本见全.如果把一道数学题比作一棵大树，那么，“题根”就是它的根系，“题根”周围的知识生长点不断推广和延伸，逐渐长成了参天大树.因此倘若我们回归课本，并且沿着课本例习题的生长点正确推导下去，便能“占领”学习数学的制高点，把握全局，轻松“玩转”数学.这也完全符合“回归课本”的学习理念，也满足了不同学生的认知需求，为学生的个性化发展提供了滋养的土壤.“把一个比较复杂的问题，‘退’到最简单最原始的问题，把这个最简单最原始的问题想通了、想透了”然后再进行归纳、综合而实现质的飞跃，“这是学好数学的一个诀窍”，引申开来，这何尝不是“教好数学的一个诀窍”.