数列的不定方程求解归类

江苏省南京市第二十九中学 (210036) 王知博 郭建华(指导教师)

数列中的不定方程是指数列中含有未知整数的等式，它的求解是数列中的一个难点.很多同学对处理数列中的不定方程问题束手无策，甚至畏惧，所以很有必要对数列中的不等方程求解进行整理和归类.本文通过具体的题目介绍不定方程的处理技巧和方法.

一、因式分解型

将所得到的方程一边化为常数，另一边化为含有未知数的代数式，并将两边分别做质因数分解和因式分解，通过讨论借助对应项相等，将方程分解成若干个方程组，以此增加方程组的个数，降低方程中未知数的次数等目的，进而求出其解.

二、范围制约型

将所得到的方程进行整理，用一个变量表示另外一个变量，借助某一变量的范围，构造不等式求解即可.

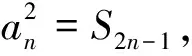
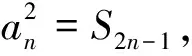
三、奇偶分析型

奇偶分析法是指通过对方程的两边是否同时取得奇数或偶数来确定方程的解的方法.一般处理数列中的方程解的存在性问题，对方程的整合变形是关键.

例3 已知各项均为正数的数列{an}的前n项和为Sn，数列{an}的前n项和为Tn，且(Sn-2)2+3Tn=4,n∈N*．(1)证明数列{an}是等比数列，并写出通项公式；(2)若an,2xan+1,2yan+2成等差数列，求正整数x,y的值．

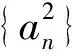
四、矛盾对立型

这种方法常用于处理数列中的存在性问题，通过对方程整合变形推出矛盾，进而说明该方程无解达到求解的目的.

例4 已知数列{an}的通项公式为an=2n-(-1)n，n∈N*．在数列{an}中是否存在某4项成等差数列？若存在，求出所有满足条件的项；若不存在，说明理由．

解析:由于an+1-an=2n+1-(-1)n+1-2n+(-1)n=2n+2(-1)n≥0，不妨设aq,ar,as,at成等差数列，其中1≤q

五、探寻约数型

探寻约数型其实就是在正整数范围内求解不定方程，将求解方程化为一边整式另一边变成分式，则分式的分子一定要满足能被分母整除，这是处理整除问题的常用方法.

求解数列中不定方程的方法有很多，在平时的学习中应对数列中的不定方程的题型进行归类，灵活选择所对应的解题方法进行求解.