随机形貌岩石节理剪切破坏分析

曹平，唐国栋，范文臣



随机形貌岩石节理剪切破坏分析

曹平，唐国栋，范文臣

(中南大学 资源与安全工程学院，湖南 长沙 410083)

基于三维高精度形貌扫描技术和节理剪切试验及数值模拟，研究随机形貌岩石节理剪切的节理表面破坏过程及机理。利用自定义参数(节理面破坏量d、破坏增量d-inc)定量分析节理面破坏过程，并基于节理表面破坏特征将随机形貌岩石节理剪切破坏过程细化为6个基本阶段。研究结果表明：节理表面破坏开始于破坏起始阶段，主要发生在整体破坏阶段，节理面整体破坏阶段的破坏量占整个剪切过程总破坏量的70%以上。节理表面破坏主要为剪胀伴随凸起体顶部剪断和沿凸起体根部剪断，前者比后者更迅速。节理面凸起体根部易产生拉伸裂纹，但整体破坏形式以剪切破坏为主。

节理；破坏过程；破坏机理；随机形貌；剪切破坏；三维数值模拟

工程岩体中存在大量节理面，节理的力学性质对岩体的力学性质有着重要影响，而节理表面的形貌特征是影响节理力学性质的主要因素。节理面的破坏在表观上表现为形貌表面凹凸体的破坏，因此，分析岩石节理剪切引起的节理面表面破坏特性对研究节理力学性质有着重要意义。Barton等[1]引入JRC表述节理面粗糙度，建立了抗剪强度公式。此后众多学者研究了剪切前后节理表面的形貌变化，提出了很多表征节理表面特征的形貌特征参数[2−4]，分析了形貌特征参数对节理抗剪强度的影响[5−7]，并建立了含有形貌特征参数的抗剪强度公式[8−10]。但这些研究都没有分析节理的剪切破坏机理和节理的表面破坏特性。王金安等[11]研究了岩石节理面在剪切前后表面损伤的分形演化。杜守继等[12]在同一花岗岩和砂岩节理试样上进行了不同垂直应力和剪切位移历史的循环剪切试验，通过计算破坏体积定量分析了节理表面的剪切破坏特性。但试验只能得到几个不同剪切位移历史的表面破坏体积，没有分析剪切过程中节理表面破坏体积的演化规律，也无法分析节理剪切的破坏机理。LI 等[13]结合声发射技术和三维形貌扫描技术研究了节理面破坏，分阶段分析了声发射事件与剪切应力−剪切位移曲线的相关关系，并研究了4个形貌参数在剪切过程中的变化规律。余华中等[14−19]利用PFC2D程序进行了二维粗糙节理剪切性质的颗粒流数值模拟，研究了节理的宏细观剪切力学行为及微裂纹的发育、演化规律和破坏机制。Nguyen等[20]结合室内试验和FLAC3D数值模拟研究了三维形貌岩石节理的剪切力学行为。由于室内直剪试验无法在剪切过程中实时捕捉节理表面破坏情况，通过试验只能得到剪切后的节理面总破坏量，无法得到节理面破坏量在剪切过程中的发展变化。本文在验证数值模拟节理面破坏分析正确性的前提下，采用FLAC3D数值模拟方法分析三维节理面剪切过程中的破坏规律及破坏机理。从节理面破坏角度出发对节理剪切破坏过程进行分阶段分析，并基于塑性区演化、单元体应变软化机制研究三维凸起体剪断机理。采用数值模拟方法进行节理表面破坏分析，通过实时捕捉剪切过程中节理面三维形貌特征分析了节理面形貌的破坏过程。

1 三维节理剪切试验及数值模拟

1.1 试件制作及数值模型的建立

采集天然花岗岩用岩石切割机加工为70 mm×70 mm×70 mm的正方体试样，并用磨石机将其各面打磨光滑。采用巴西劈裂法将完整岩石沿轴线方向对称劈裂，制作人工岩石节理试样，见图1(a)。选用英国Taylor Hobson公司生产的Talysurf CLI 2000 三维表面形貌测试仪进行节理表面三维形貌量测，所得三维节理面见图1(b)。利用三维表面形貌测试仪获取的点云数据生成节理面网格，进而建立三维数值模型，见图1(c)。

试验所用花岗岩的基本力学参数根据室内试验确定，取值见表1。数值模型采用Mohr-Coulomb应变软化本构，参考沈华章等[21]提出的花岗岩应变软化参数的计算方法，应变软化模型参数的选取如表2所示。

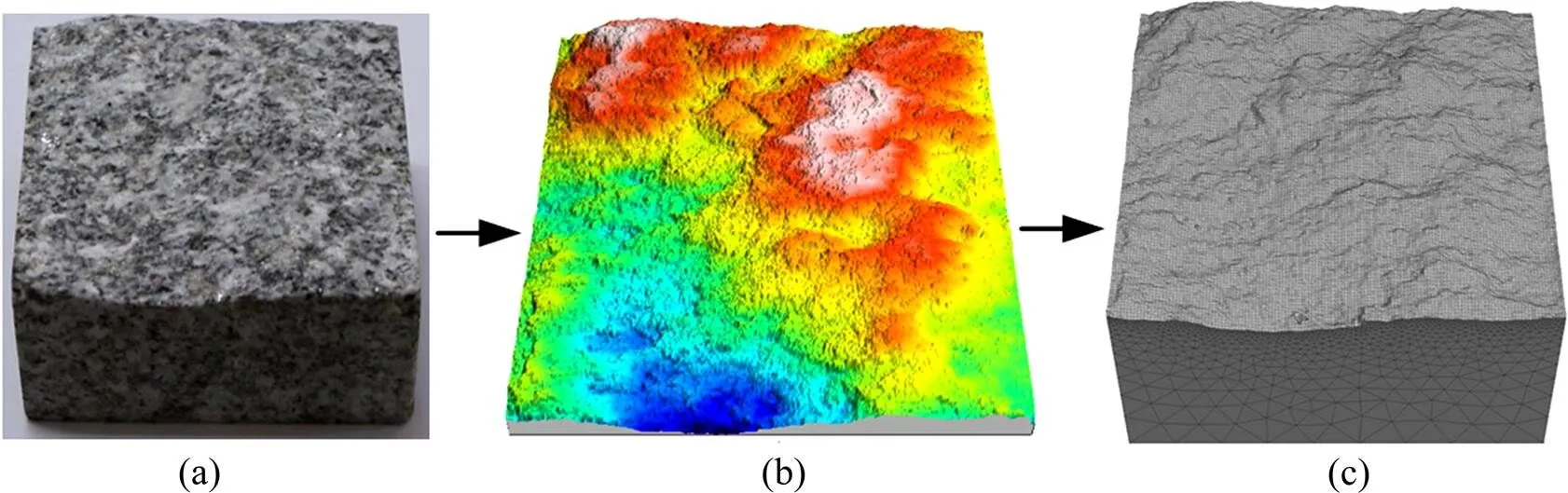
(a) 节理试件；(b) 节理三维形貌；(c) 节理三维模型

相比以往大量用于节理剪切数值模拟中的根据JRC值建立的简化模型和利用剖面线建立的二维节理模型，三维节理面模型更接近于工程实例中节理面的真实形貌，能更真实地反映三维形貌对岩石节理力学特性的影响。

表1 花岗岩基本力学参数

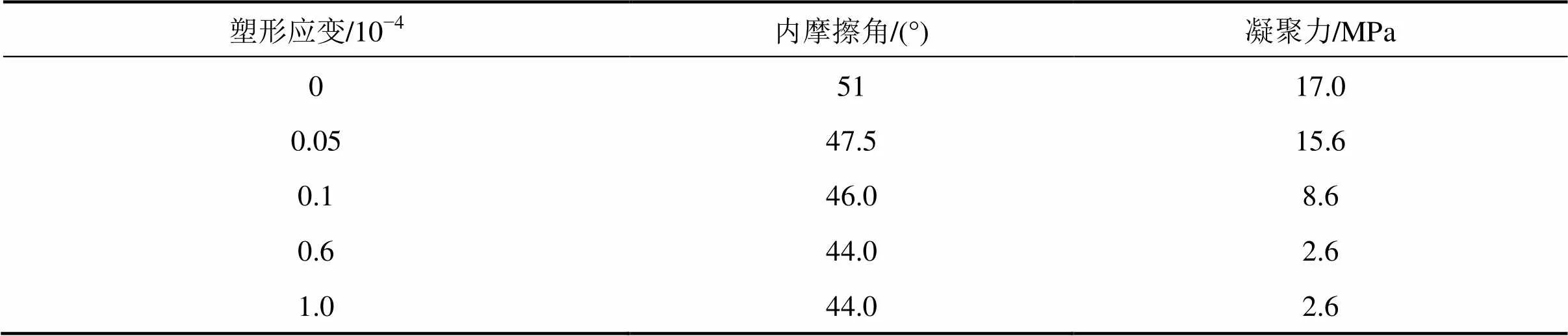
表2 数值模型软化参数

1.2 直剪试验及数值模拟

分别对节理试样及模型进行1，3和5 MPa法向荷载下的直剪试验和数值模拟。直剪试验在RYL−600岩石剪切流变仪上进行，剪切速率为0.6 mm/min，试验过程中记录法向位移、剪切位移、剪应力和应变等参数。为了真实模拟直剪试验中试件的应力状态，数值计算模型的边界条件如图2所示。以上部模型顶面节点的法向位移平均值作为法向位移；以上部模型左面节点的剪切方向位移平均值作为剪切位移；以下部模型右面节点的不平衡力之和与试件剪切面积之比作为剪切应力。

在FLAC3D数值模拟中，三维节理面的力学特性可运用interface接触单元来实现，采用Coulomb滑移本构，其力学性能由黏结力，内摩擦角，法相刚度k，剪切刚度k和抗拉强度等力学参数共同控制。因为本文所用节理面为非黏性贯通无填充节理面，故黏结力、抗拉强度、剪胀角均取为0。其他参数均基于室内试验进行标定。

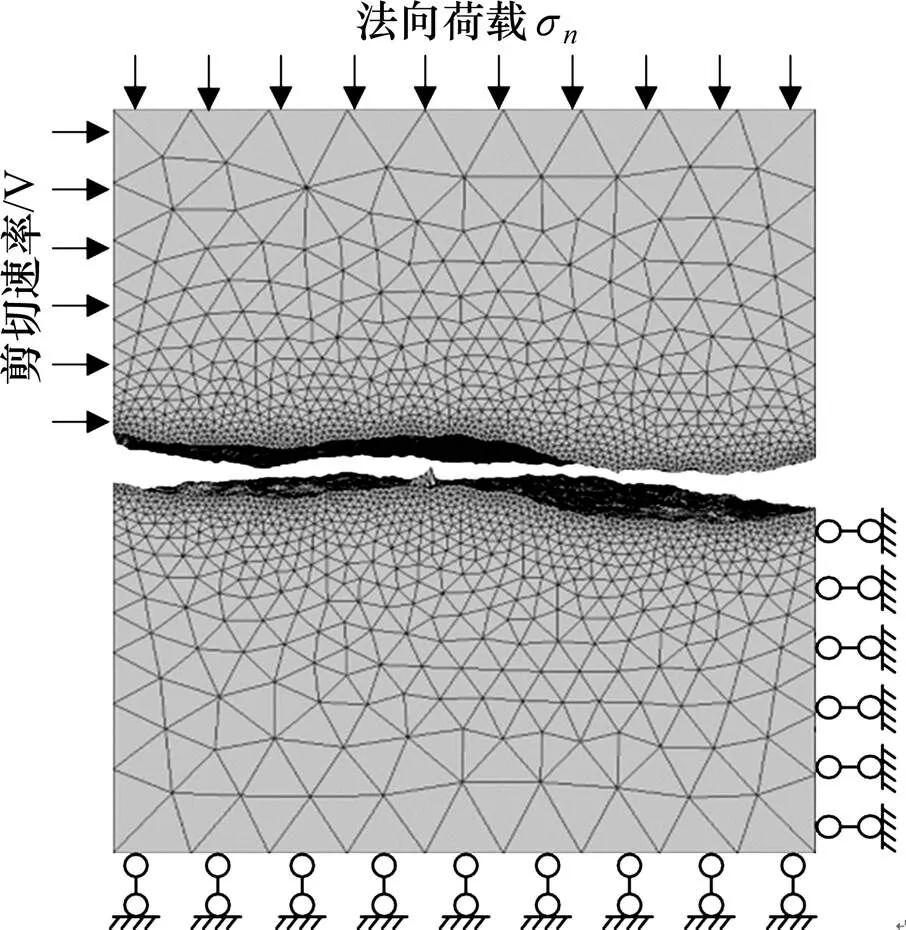
图2 三维节理剪切试验的数值模拟

根据Bandis等[22]提出的法向刚度标定方法，通过平直节理闭合试验，得出法向刚度k的值。采用Vallier等[23]的研究中给出的方法，基于平直节理剪切试验结果对k值进行标定。和的取值通过平直节理剪切实验得出。根据以上方法，本文所用节理面模型的力学参数如表3所示。

表3 节理面模型力学参数

1.3 试验结果分析

图3和图4给出了G1，G2和G3节理分别在1，3和5 MPa法向应力下直剪试验的剪切应力−剪切位移曲线和剪胀曲线，以及相应的FLAC3D数值试验结果。由图3和图4可知，直剪试验与数值试验结果呈现相同规律。剪切应力−剪切位移曲线中，不同法向荷载下弹性阶段曲线基本重合，峰值强度随法向荷载的增加而增大，峰后曲线下降至残余剪切强度，残余剪切强度随法向荷载的增加而增大。剪胀曲线中法向位移随剪切位移的增大而增大，且法向位移不仅与法向荷载有关，还与节理面形貌特征有关。虽然G3的法向荷载最大，但剪胀大于G2，这是由于节理面形貌不同而引起的。数值试验的峰值强度、残余强度、剪胀位移及剪应力曲线和剪胀曲线的趋势均与直剪试验结果保持一致。

图3 剪切应力–剪切位移曲线

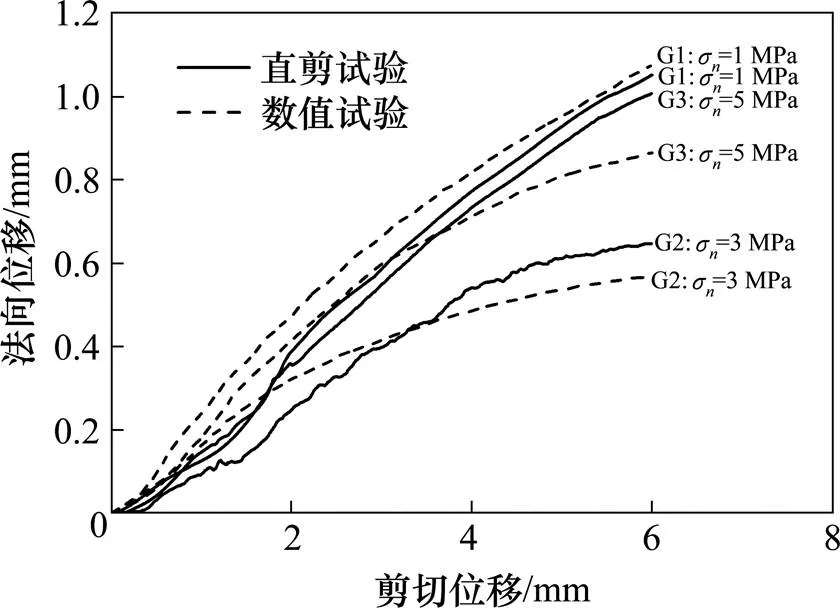
图4 剪胀–剪切位移曲线

以上分析表明，数值试验与直剪试验结果都非常吻合，证明三维形貌节理模型的数值试验能真实反映三维岩石节理的剪切力学特性。

2 节理面破坏分析

2.1 节理面破坏

节理剪切过程中，由于节理面上的凸起体形态的不均匀，导致了节理面上应力的不均匀分布，从而引起各凸起体先后发生剪断或磨损，即为节理表面破坏。

节理表面破坏可通过将节理剪切前后的形貌高度数据相减求得的形貌差值图像来显现，该形貌差值图像可真实、形象、直观地反映节理面破坏情况，限于篇幅，仅以G2节理为例，如图5(a)，5(b)和5(c)所示。由图可知，节理面破坏主要为小区域内陡峭凹凸体的破坏。

在FLAC3D数值模拟中，定义塑性应变达到0.6×10−4的单元体为已破坏的单元体。在节理剪切过程中，定义已发生破坏的单元体体积之和为破坏量d，量纲为m3。破坏量d越大，即节理表面发生破坏的凸起体越多，节理面破坏程度越大。剪切后已破坏的单元体用红色表示，用以呈现节理面破坏状态，见图5(d)。

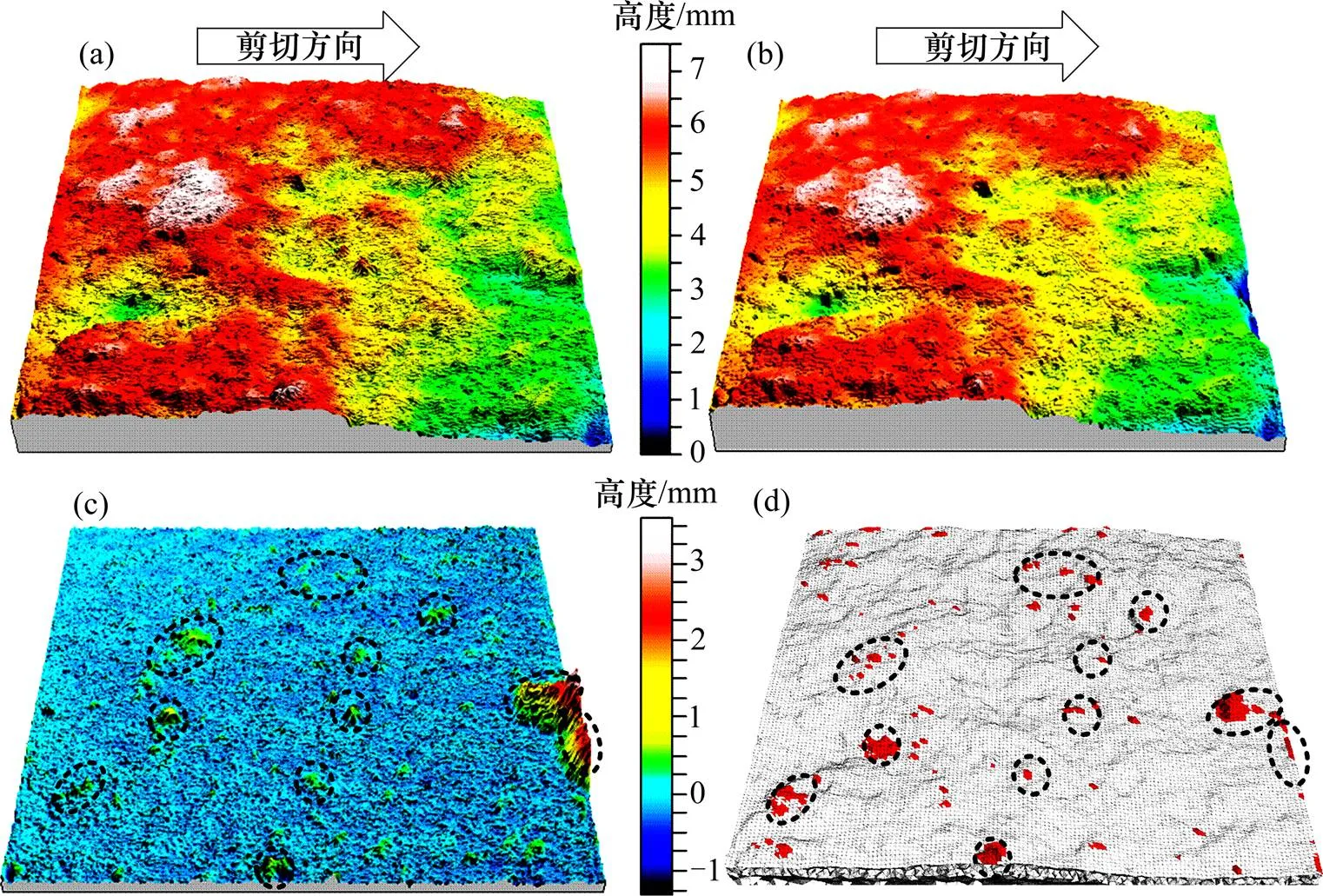
(a) 剪切前节理形貌；(b) 剪切后节理形貌；(c) 剪切前后形貌差值；(d) 数值模拟剪切后破坏单元体

为了验证数值模拟用于节理面破坏分析的正确性，进行了破坏区域及破坏量的对比分析。在图5(c)和5(d)中，将几处较大的形貌破坏用虚线圈出，对比可知，在破坏区域方面，数值试验与剪切试验结果保持较高的一致性。计算3组试验与数值模拟的节理面破坏量，列于表4。定量比较可知，数值模拟结果与试验值的误差也相对较小。以上分析可作为进一步研究剪切过程中节理面破坏规律与破坏机理的依据。

表4 破坏量的试验与数值模拟结果

2.2 破坏过程分析

定义每0.1 mm剪切位移内的节理面破坏量为破坏增量d-inc，用来描述节理面破坏速率。破坏增量d-inc越大，即单位剪切位移内节理表面凸起体破坏越多，节理面破坏速率越快。破坏增量d-inc节理面的破坏过程分析以G3节理为例，图6为G3节理数值剪切试验的剪切应力、破坏增量与剪切位移的关系，并选取4个剪切过程中具有代表性的节理面破坏状态，见图7。

图6 剪切应力、破坏增量与剪切位移的关系

(a) B点剪切位移=0.9 mm；(b) C点剪切位移=1.1 mm=1.1 mm；(c) D点剪切位移=3.2 mm；(d) E点剪切位移=6.0 mm

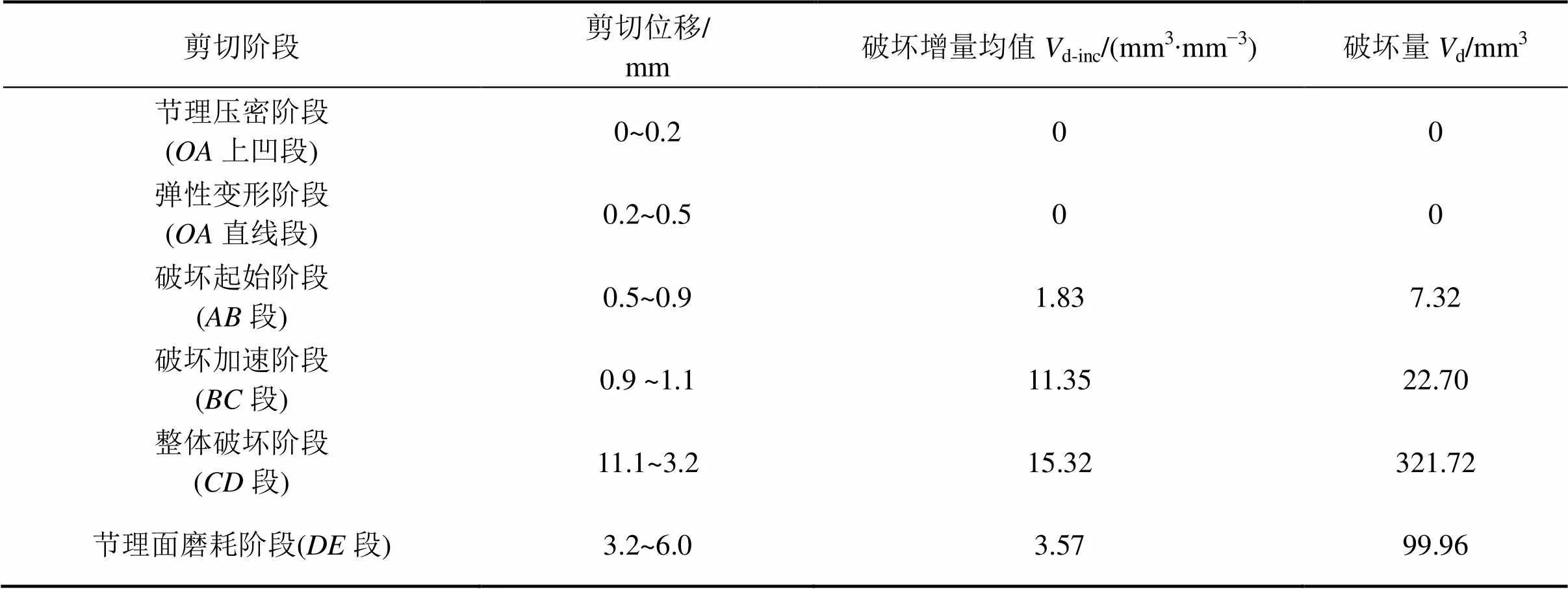
表5 各阶段节理面破坏量

对节理面破坏过程进行分段分析，各阶段节理面破坏增量均值和破坏量见表5，结合图6和图7可知，节理面破坏量与剪切应力之间存在如下对应关系：

1)图6中段包含前半段的上凹曲线和后半段的近似直线，分别为节理压密阶段和弹性变形阶段，该段范围内未出现节理面破坏。

2) 节理面在点处开始出现破坏，直至点，破坏增量逐渐增加，但总体破坏量依然较小，只有7.32 mm3。由图7(a)可知，在段破坏的节理面单元体为零散分布的少量体积小、高径比大的微凸体，可将段称为破坏起始阶段。

3)段节理面破坏速率急剧增大，破坏增量均值达到11.35 mm3，比上一阶段增大了9.52 mm3。点处剪切位移为1.1 mm，剪切应力达到峰值强度。对比图7(a)和7(b)可知，在段节理面发生了几处较大的破坏，且该段的剪切位移只有0.2 mm，故将段称为破坏加速阶段。

4)段，剪切应力过了峰值后明显下降，节理面破坏增量维持较高值，增量均值为15.32 mm3，该阶段节理面破坏量最大，有321.72 mm3，占整个剪切过程中破坏总量的71.22%。至点时节理面破坏量如图7(c)所示，故称段为整体破坏阶段。

5)点后剪切应力趋于平稳，逐渐达到残余剪切强度，节理面破坏增量逐渐减小并趋于稳定。该阶段破坏增量均值为3.57 mm3，仅为整体破坏阶段的23.3%。对比图7(c)和7(d)可知，该阶段仅有少许零碎破坏，故点后称为节理面磨耗阶段。

以上分析根据剪切过程中节理面破坏增量、破坏量的变化规律及其与剪切应力−剪切位移的对应关系，将三维形貌节理剪切过程分为6个基本阶段：节理压密阶段、弹性变形阶段、破坏起始阶段、破坏加速阶段、整体破坏阶段和节理面磨耗阶段。

破坏加速阶段破坏的微凸体分布零散，容易剪断，对节理面抗剪强度的影响非常小；节理面破坏主要发生在抗剪强度之后的节理面整体破坏阶段，该阶段破坏量占全过程破坏量的70%以上；整体破坏后节理面磨耗阶段只有少部分节理面单元体被磨损，剪切应力基本上全部来自节理表面摩擦力。

2.3 破坏机理分析

节理面破坏机制有渐进的磨耗和急剧的凹凸体剪断破坏，且凹凸体剪断破坏为主，约占整个破坏区域的70%~80%[12]。节理面渐进磨耗为残余剪切阶段的主要破坏机制，凹凸体剪断破坏从机理上可分为剪胀伴随凸起体顶部剪断和沿凸起体根部剪断2种破坏模式。

图8为一个凸起体发生剪胀伴随凸起体顶部剪断的塑性区演化图。该凸起体的破坏出现在峰值前的破坏加速阶段，主要发生在节理面整体破坏 阶段。

由图8可知，剪切位移达到0.90 mm时，凸起体面向剪切方向一侧的底部开始发生拉应变，顶部发生塑性剪应变。随着剪切的进行，拉应变区逐渐向凸起体底部中央扩展，塑性剪应变区向底部边缘扩展，还未发生凸起的破坏；剪切位移达到1.00 mm时，凸起体顶部单元体发生剪切破坏。剪切位移达到1.70 mm时，凸起体底部部分单元体发生拉伸破坏，但法向荷载及凸起体坡面角不足以阻止剪胀现象，拉伸裂纹并未沿凸起体底部扩展，所以凸起体的主要破坏仍为顶部处于塑性剪应变区的单元体随着剪胀的进行逐渐被剪断。剪切位移达到3.20 mm时，拉应变区已扩展至凸起体中部，塑性剪应变区阻碍剪胀现象的单元体已完全被剪断，可视为该凸起体完全破坏。整个凸起体破坏过程的剪切位移增量有2.20 mm。凸起体根部有少量单元体发生拉伸破坏，顶部随剪胀被剪断的单元体破坏模式基本都是剪切破坏。

图9为一个凸起体发生沿凸起体根部剪断的塑性区演化。该凸起体的破坏发生在破坏起始阶段及峰值前的破坏加速阶段。

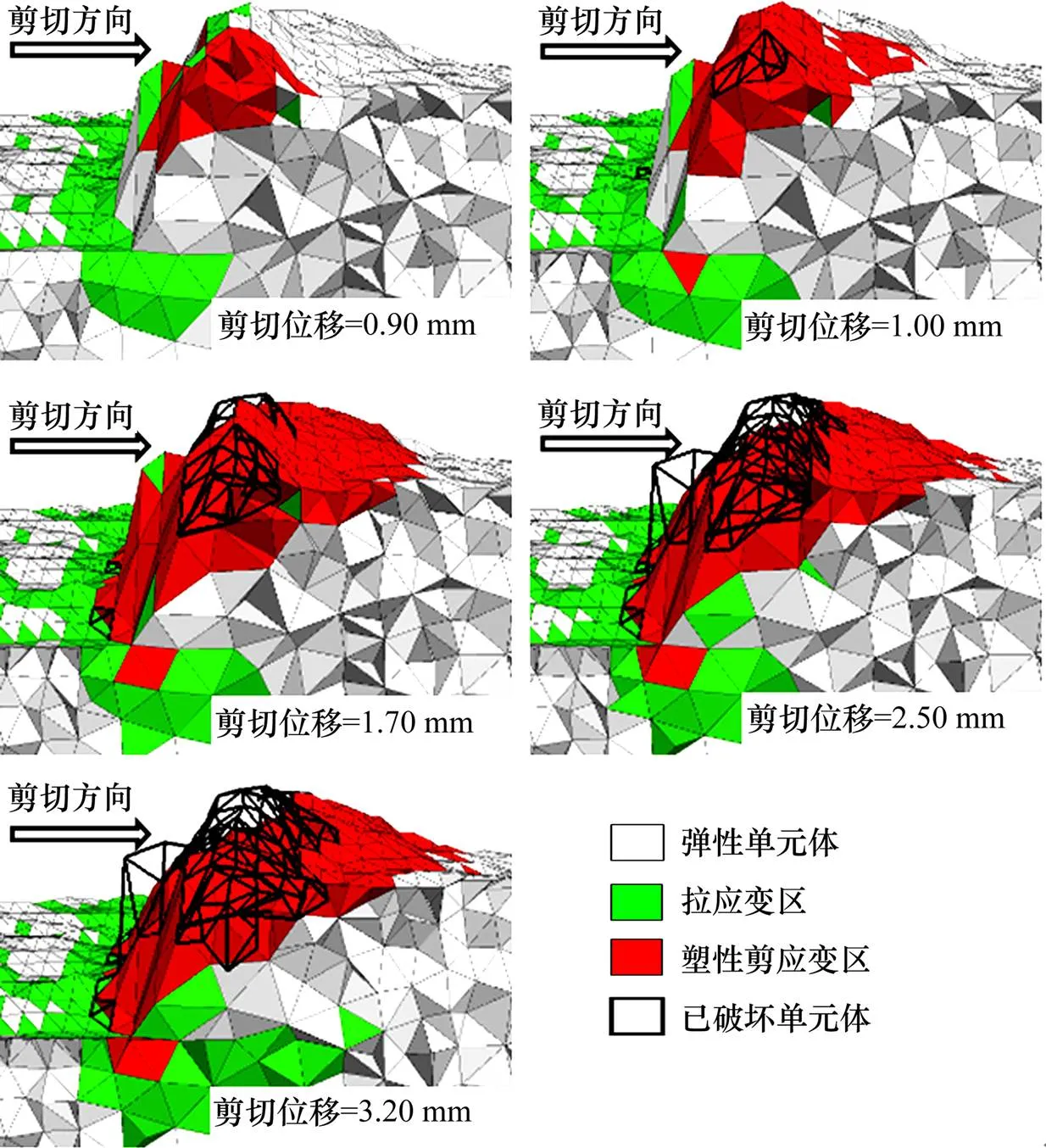
图8 剪胀伴随凸起体顶部剪断的塑性区演化图

图9 沿凸起体根部剪断的塑性区演化图

由图9可知，剪切位移达到0.6 mm时，凸起体面向剪切方向根部单元体已有拉应变，随后拉应变区从根部沿圆弧形向凸起体底部中心扩展，根部少量单元体发生拉伸破坏，凸起体坡面发生塑性剪应变，塑性剪应变区紧贴拉应变区沿剪切方向扩展，如剪切位移为0.75 mm时塑性区图所示。此后单元体的破坏模式也逐渐从拉伸破坏转为剪切破坏，剪切位移为1.00 mm时，破坏单元体基本都处于塑性剪应变区。单元体破坏继续快速扩展贯通整个凸起体底部，剪切位移达到1.10 mm时，凸起体整体与岩石试件分离，造成破坏。整个凸起体破坏过程的剪切位移增量只有0.35 mm。破坏初期凸起体根部单元体表现为拉伸破坏，随后破坏区域集中在塑性剪应变区，即大部分单元体的破坏模式为剪切破坏。

通过以上分析可知，凸起体发生剪胀伴随凸起体顶部剪断时的剪切位移增量比发生沿凸起体根部剪断时大很多，说明沿凸起体根部剪断比剪胀伴随凸起体顶部剪断破坏速度快很多；凸起体的根部易产生拉伸裂纹，即使是剪胀伴随凸起体顶部剪断的破坏模式，凸起体的根部也可能产生较小的拉伸裂纹，只是拉伸裂纹并未进一步扩展贯通造成凸起体的整体分离。2种破坏机理下单元体的破坏形式均以剪切破坏为主。

3 结论

1) 基于三维扫描技术与数值模拟相结合的方法，进行了岩石节理剪切过程中的节理面破坏研究，通过实时捕捉剪切过程中节理面的三维形貌特征分析了节理面形貌的破坏过程。

2) 提出使用破坏量d和破坏增量d-inc定量分析节理剪切破坏过程，结合剪切过程中节理面破坏量的发展变化，将三维形貌节理剪切破坏过程细化为6个基本阶段：节理压密阶段、弹性变形阶段、破坏起始阶段、破坏加速阶段、整体破坏阶段和节理面磨耗阶段。

3) 节理面破坏过程分析表明节理面破坏开始于破坏起始阶段，该阶段破坏的节理面单元体为零散分布的少量体积小、高径比大的微凸体，对节理面的剪切强度没有影响；剪切应力达到峰值前有凸起体破坏速率急剧增大现象；节理表面破坏主要发生在峰值后的整体破坏阶段；节理面磨耗阶段只有少部分节理表面单元体被磨损，剪切应力基本上全部来自节理表面摩擦力。

4) 沿凸起体根部剪断比剪胀伴随凸起体顶部剪断更迅速；凸起体的根部易产生拉伸裂纹，但整体破坏形式仍以剪切破坏为主。

[1] Barton N, Choubey V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1977, 10(1/2): 1−54.

[2] Belem T, Homand-Etienne F, Souley M. Quantitative parameters for rock joint surface roughness[J]. Rock Mechanics and Rock Engineering, 2000, 33(4): 217−242.

[3] Homand F, Belem T, Souley M. Friction and degradation of rock joint surfaces under shear loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(10): 973−999.

[4] Riss J, Gentier S, Sirieix C, et al. Degradation characterization of sheared joint wall surface morphology[C]// Proceedings of the 2nd North American Rock Mechanics Symposium. [S. l.]:[s. n.], 1996: 1343− 1349.

[5] 曹平, 范祥, 蒲成志, 等. 节理剪切试验及其表面形貌特征变化分析[J]. 岩石力学与工程学报, 2011, 30(3): 480–485. CAO Ping, FAN Xiang, PU Chengzhi, et al. Shear test of joint and analysis of morohology characteristic evolution of joint surface[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 480−485.

[6] 曹平, 贾洪强, 刘涛影, 等. 岩石节理表面三维形貌特征的分形分析[J]. 岩石力学与工程学报, 2011, 30(增2): 3839−3843. CAO Ping, JIA Hongqiang, LIU Taoying, et al. Fractal analysis of three-dimensional topography characteristics of rock joint surface[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Suppl 2): 3839– 3843.

[7] 曹平, 何云, 范祥, 等. 剪切前后节理表面形貌纹理特征变化[J]. 中南大学学报, 2013, 44(11): 4624−4630. CAO Ping, HE Yun, FAN Xiang, et al. Evolution of morphology texture characteristics based on rock joints shear tests[J]. Journal of Central South University, 2013, 44(11): 4624−4630.

[8] Grasselli G. Shear strength of rock joints based on quantified surface description[D]. Switzerland: Swiss Federal Institute of Technology, 2001.

[9] 夏才初, 唐志成, 宋英龙.基于三维形貌参数的偶合节理峰值抗剪强度公式[J]. 岩石力学与工程学报, 2013, 32(增1): 2833−2839. XIA Caichu, TANG Zhicheng, SONG Yinglong. A new peak shear strength formula for matching irregular joints based on 3D morphology parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 32(Suppl 1): 2833−2839.

[10] 唐志成, 黄润秋, 张建明, 等. 含坡度均方根的节理峰值剪切强度经验公式[J].岩土力学, 2015, 36(12): 3433−3438. TANG Zhicheng, HUANG Runqiu, ZHANG Jianming, et al. Empirical peak shear strength criterion for rock joints based on slope root-mean-square[J]. Rock and Soil Mechanics, 2015, 36(12): 3433−3438.

[11] 王金安, 谢和平. 岩石节理面在剪切中表面损伤的分形演化[J]. 力学与实践, 1997, 19(4): 56−58, 55. WANG Jinan, XIE Heping. Fractal evolution of surface damage of rock joints during shearing[J]. Mechanics in Engineering, 1997, 19(4): 56−58, 55.

[12] 杜守继, 江崎哲郎, 蒋宇静, 等. 岩石节理的剪切破坏特性的定量分析[C]// 中国岩石力学与工程学会第五次学术大会论文集. 北京: 中国科学技术出版社, 1998: 239−244. DU Shouji, Tetsuro E, JIANG Yujing, et al. The quantitative evaluation of surface damage of rock joint during shear processes[C]// The 7th Academic Congress of Chinese Society for Rock Mechanics and Engineering. Beijing: China Science and Technology Press, 1998: 239−244.

[13] LI Kaihui, CAO Ping, ZHANG Ke, et al. Macro and meso characteristics evolution on shear behavior of rock joints [J]. Journal of Central South University, 2015, 22(8): 3087−3096.

[14] 余华中, 阮怀宁, 褚卫江. 岩石节理剪切力学行为的颗粒流数值模拟[J]. 岩石力学与工程学报, 2013, 32(7): 1482−1490. YU Huazhong, RUAN Huaining, CHU Weijiang. Particle flow code modeling of shear behavior of rock joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(7): 1482−1490.

[15] 余华中, 阮怀宁, 褚卫江. 弱化节理剪切力学特征的颗粒流模拟研究[J]. 岩土力学, 2016, 37(9): 2712−2720. YU Huazhong, RUAN Huaining, CHU Weijiang. Particle flow modeling of shear character of weakened joint[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 37(9):2712-2720.)

[16] 夏才初, 宋英龙, 唐志成, 等. 粗糙节理剪切性质的颗粒流数值模拟[J]. 岩石力学与工程学报, 2012, 31(8): 1545–1552. XIA Caichu, SONG Yinglong, TANG Zhicheng, et al. Particle flow numerical simulation for shear behavior of rough joints[J]. Rock and Soil Mechanics, 2012, 31(8): 1545−1552.

[17] 宋英龙, 夏才初, 唐志成, 等. 不同接触状态下粗糙节理剪切强度性质的颗粒流数值模拟和试验验证[J]. 岩石力学与工程学报,2013, 32(10): 2028−2035. SONG Yinglong, XIA Caichu, TANG Zhicheng, et al. Numerical simulation and test validation for direct shear properties of rough joint under different contact states[J]. Rock and Soil Mechanics, 2013, 32(10): 2028−2035.

[18] 周喻, Misra A, 吴顺川, 等. 岩石节理直剪试验颗粒流宏细观分析[J]. 岩石力学与工程学报, 2012, 31(6): 1245−1256. ZHOU Yu, Misra A, WU Shunchuan, et al. Macro and meso-analyses of rock joint direct shear test using particle flow theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1245−1256.

[19] 曹日红, 曹平, 林杭, 等. 不同粗糙度的节理直剪颗粒流分析[J]. 岩土力学, 2013, 34(增2): 456−463. CAO Rihong, CAO Ping, LIN Hang, et al. Particle flow analysis of direct shear tests on joints with different roughnesses[J]. Rock and Soil Mechanics, 2013, 34(Suppl 2): 456−463.

[20] Nguyen V M, Konietzky H, Frühwirt T. New methodology to characterize shear behavior of joints by combination of direct shear box testing and numerical simulations[J]. Geotechnical and Geological Engineering, 2014, 32(4): 829−846.

[21] 沈华章, 王水林, 刘泉声. 模拟应变软化岩石三轴试验过程曲线[J]. 岩土力学, 2014, 35(6): 1647−1654. SHEN Huazhang, WANG Shuilin, LIU Quansheng. Simulation of constitutive curves for strain-softening rock in triaxial compression[J]. Rock and Soil Mechanics, 2014, 35(6): 1647−1654.

[22] Bandis S, Lumsden A C, Barton N R. Experimental studies of scale effect on the shear behaviour of rock joints[J]. International Journal of Rock Mechanics & Mining Sciences Geomechanics Abstracts, 1981, 20: 249−268.

[23] Vallier F, Mitani Y, Boulon M, et al. A Shear model accounting scale effect in rock joints behavior[J]. Rock Mechanics and Rock Engineering, 2010, 43(5): 581−595.

Shear failure analysis of rock joint with random morphology

CAO Ping, TANG Guodong, FAN Wenchen

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

The shear failure process and mechanism of Joint surface with random morphology rock joint was investigated, based on 3D high precision morphology scanning technique and joint shear test and numerical simulation. Damage evolution process of joint surface was quantitative analysis using the failure quantity (d) and the failure increment (d-inc), and the shear process of random morphology rock joint was divided into six basic stage based on the joint surface damage evolution characteristics. The results show that the joint surface damage begin in initial stage of destruction, and mainly in the whole failure stage, joint surface damage in the whole failure stage account for more than 70% of the whole shear process. Joint surface damage mainly the dilation with shearing at the top of the convex and the shearing along the convex root, and the former is more rapid than the latter.

joint; failure process; failure mechanism; random morphology; shear failure; three-dimensional numerical simulation

10.19713/j.cnki.43−1423/u.2019.02.012

TU452

A

1672 − 7029(2019)02 − 0367 − 09

2018−01−24

国家自然科学基金资助项目(11772358)；中南大学研究生创新项目(2016zzts461)

曹平(1977−)，男, 湖南衡阳人, 教授，从事岩石力学、断裂力学方面研究；E−mail：pcao_csu@sina.com

(编辑 涂鹏)