宝兰客专路堤段地面振动特性试验研究与数值分析
2019-03-07马骙骙李斌王东白广明
马骙骙,李斌,王东,白广明
宝兰客专路堤段地面振动特性试验研究与数值分析
马骙骙,李斌,王东,白广明
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
基于高速列车动荷载激励引起的无砟轨道-路基-黄土地基体系的地面振动问题,对宝兰客专DK993+110处路堤区段地面振动进行试验研究和数值分析。对试验数据从时域和频域2个方面进行分析,研究不同车型的动荷载引起地面垂向振动加速度在黄土地基中的衰减规律,研究结果表明;在距离线路中心线10~24 m衰减较快,随着距离增大,距离线路中心线24~42 m衰减速度趋于平缓,且在30~42 m处各型车引起地面振动均出现了振动反弹增大现象。建立车辆-轨道-地基系统模型,研究列车动荷载作用下的地面响应,发现与实测结果吻合良好,验证模型的合理性与计算的正确性,依据不同场地速度结构,通过改变地基介质模量比和覆盖层厚度的方式,分析地基介质模量比和覆盖层厚度对振动反弹增大的影响。分析车速对地面振动的影响,发现地面振动随车速增大呈增大趋势,且不同车速列车引起振动反弹区域也有一定差异。按《城市区域环境振动标准》评价该处地面振动Z振级,回归分析得出各型车引起Z振级符合对数衰减规律,但在振动反弹区30~42 m处拟合效果较差,表明拟合公式适用范围应当限定在10~30 m之间。
高速铁路;地面振动;现场试验;数值分析;振动反弹
铁路交通所引起的地面振动与现场地质条件、列车类型以及线路断面形式等因素密切相关。为此,人们对铁路交通引起的地面振动进行了很多研究,这些研究均表明地面振动随距离衰减的一般规律[1−2],但很多实测结果和理论研究也发现地面振动并不是单调减小的,在一定区域会出现反弹增大现象,导致振动波能量在阻尼作用下逐渐衰减的一般规律在反弹增大区域不再适用。为了分析地面振动的衰减规律和引起反弹增大的机理,马蒙等[3]通过地面落锤试验发现地表体波和瑞利波衰减速度不同是引起地面振动的波动式衰减的原因;郑鑫等[4]通过三维层状场地的格林函数研究了单一频率激励时不同场地速度结构对地面振动衰减过程中反弹增大的影响,Fujikake[5]认为与土层固有频率相近的振源激励的频率会引起地表振动的反弹增大。这些研究虽从不同角度分析了地面振动规律,但缺乏与实际铁路现场情况的结合,因此有必要结合具体工况,采用数值方法进行分析。为了考察宝兰客专高速列车运行状态下不同车型引起的地面振动在黄土地基中的横向衰减规律,本文对宝兰客专DK993+110处通过的3种典型车型CRH380B,CRH5G和CRH2G引起的地面振动进行试验研究,基于试验结果和现场工况指导有限元建模,对该处高速列车引起地面振动特性进行分析,并采用数值试验的方法,结合波的传播理论,分析实测结果中地面振动随距离衰减的一般规律,并对一定区域出现的振动反弹增大现象的成因和影响因素进行 探讨。
1 现场测试方案
1.1 测点布设方案
依据我国城市区域地面振动评价的规范要 求[5],铁路干线两侧(铁路外轨两侧30 m外)昼夜间地面振动Z振级不应大于80 dB,测试场地横向取距线路中心线42 m,可以覆盖铁路外轨两侧30 m的测试范围,依次布设6个测点,布点位置如图1所示。
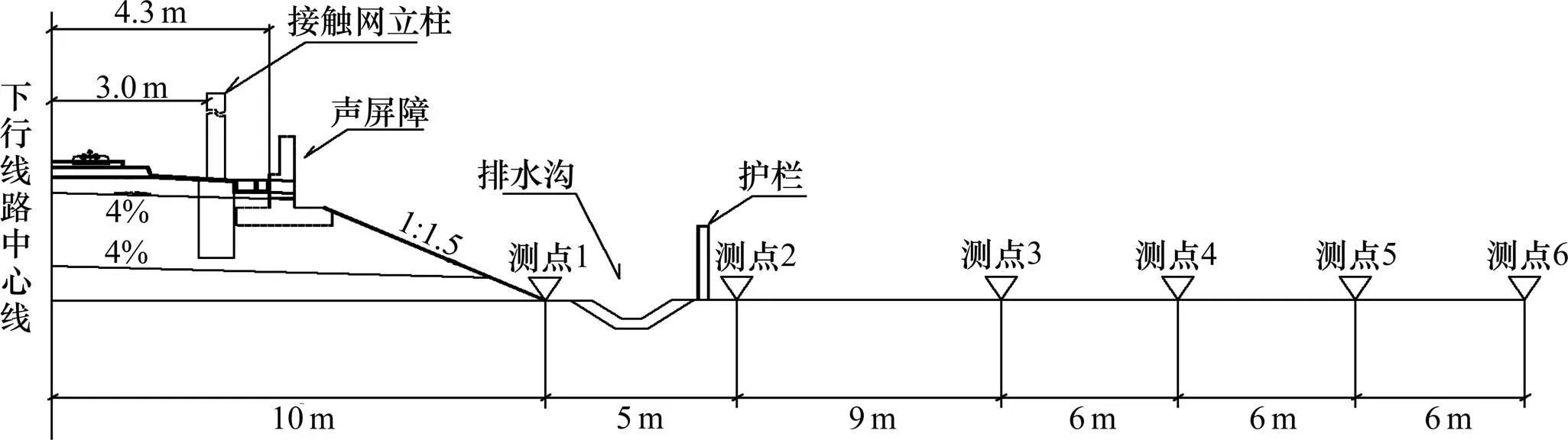
图1 测点布置示意图
1.2 现场概况与测试仪器
测试地点位于宝兰客专DK993+110处,该段为CRTSⅠ型双块式无砟轨道路堤段,沿线路两侧方向地势平坦开阔,便于布设测点。地基土层由素填土、粉状黄土组成。试验仪器为东方所INV3062C型24位采集仪,配套加速度传感器,采样频率为1 024 Hz。考虑到地面振动评价多以垂向响应为指标,在垂向设置加速度传感器。
1.3 车辆特征
现场共采集30列动车数据,从中选取有速度差异的CRH5G 2列,再选取CRH2G和CRH380B各一列作为分析对象,相对采集器均为近轨,保证了振源位置的一致性,CRH5G按车速大小编号为1号和2号。现场通过记录列车通过测段的时间计算出列车速度。各列车参数及实测速度如表1所示。

表1 列车通过情况统计表
2 测试结果分析
2.1 地面振动加速度时程响应
现场试验对3种车型在以上6个测点处的地面垂向加速度时程响应均进行了测试,限于篇幅,如图2所示,这里主要对时速245 km/h的CRH5G(1号)列车在10,24,30和42 m处引起的振动进行 分析。
对该处地面振动垂向加速度时程响应的测试结果表明,CRH5G列车在各测点的振动持续时间基本一致,在距线路中心线10m处,如图3所示,随着列车通过该测试断面,振动加速度出现由单个转向架作用产生的明显的周期性峰值,随着距线路中心线距离的增加,加速度在24m处发生显著衰减,在30m处已经不能分辨明显的周期性峰值,振动衰减速度也呈减缓趋势。

(a) 10 cm;(b) 24 cm;(c) 30 m;(d) 42 m
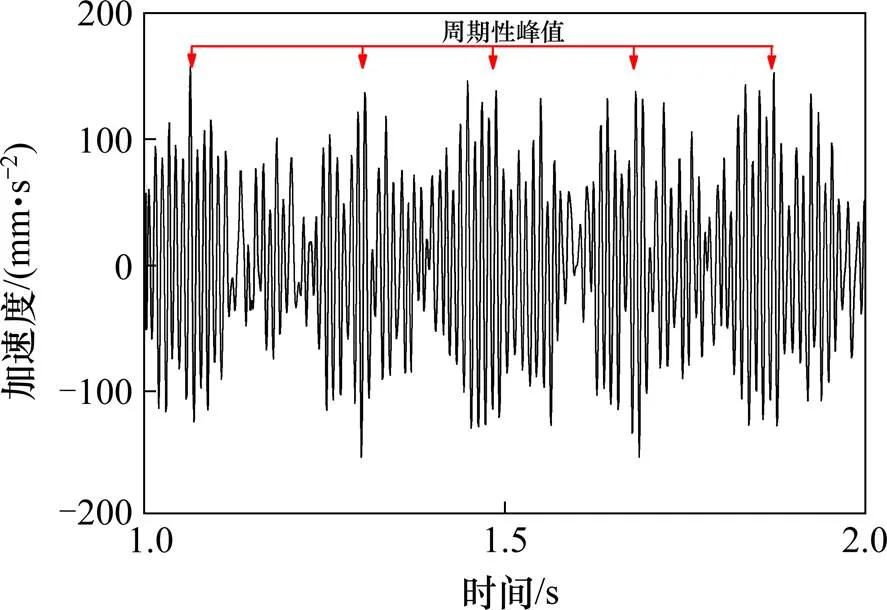
图3 10 m处地面垂向振动加速度时程曲线局部放大图
2.2 振动频域响应测试结果及分析
对振动加速度时程响应数据进行傅里叶变换并滤去现场存在的50 Hz工频干扰,得到地面振动的频谱数据,图3为时速245 km/h的CRH5G列车通过时地面振动加速度频谱图。

(a) 10 cm;(b) 24 cm;(c) 30 m;(d) 42 m
频谱分析表明,10 m处频谱内出现多个单峰值,主频在100 Hz左右,且有150 Hz以上的高频成分出现,证明振动能量在频域内分布较分散。随着距离的增大,地面振动加速度幅值逐渐衰减,主要体现在高频成分被抑制,24 m和30 m处的高频成分已经明显衰减,在24 m处25~50 Hz的振动出现了反弹增大现象,到了距线路中心线42 m处,100 Hz以上的振动能量已经很小,主要由25~50 Hz的低频成分起作用。图4中10 m处的主频主要是由轨枕间距作用率(68.06/0.65=104.7 Hz)引起,24 m后的频谱主要由移动轴重作用率(60.08/2.7=25.2 Hz)引起。
2.3 振动波在土体中随距离的衰减特性
为了分析不同车型在不同速度下引起地面振动随距离衰减的规律,以加速度峰值||max和加速度有效值rms为指标来衡量地基土体振动响应,对于离散采样:

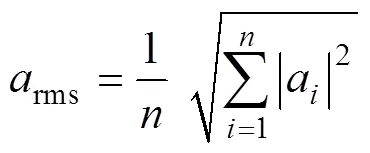
式中:为采样点的个数。由式(1)和式(2)求得的不同车型加速度峰值和加速度有效值如图5和图6 所示。

图5 加速度峰值曲线
由图5和图6可以看出,各车型加速度峰值和加速度有效值变化规律基本一致,随距离增大并不是呈单调衰减趋势,在距线路中心线30~42 m处均出现了加速度的反弹增大现象,其中CRH5G(1号)出现在36 m处,CRH5G(2号)出现在42 m处,不同车速的两列车加速度反弹增大出现在不同位置,表明出现“振动反弹”位置与车速相关,在42 m处,时速228 km/h的2号车引起的地面振动加速度甚至比时速245 km/h的1号车要大,说明振动反弹现象应该引起足够的重视。从衰减速率来看,10~24 m衰减较快,随着距离增大趋于平缓。除了反弹区以外,CRH5G较大速度的1号车加速度曲线在各测点处均在2号车上方,说明同一车型速度越大,引起地面振动加速度越大。CRH2G和CRH380B时速均为220 km/h,但由于CRH380B轴重较大,故引起地面振动加速度较大。
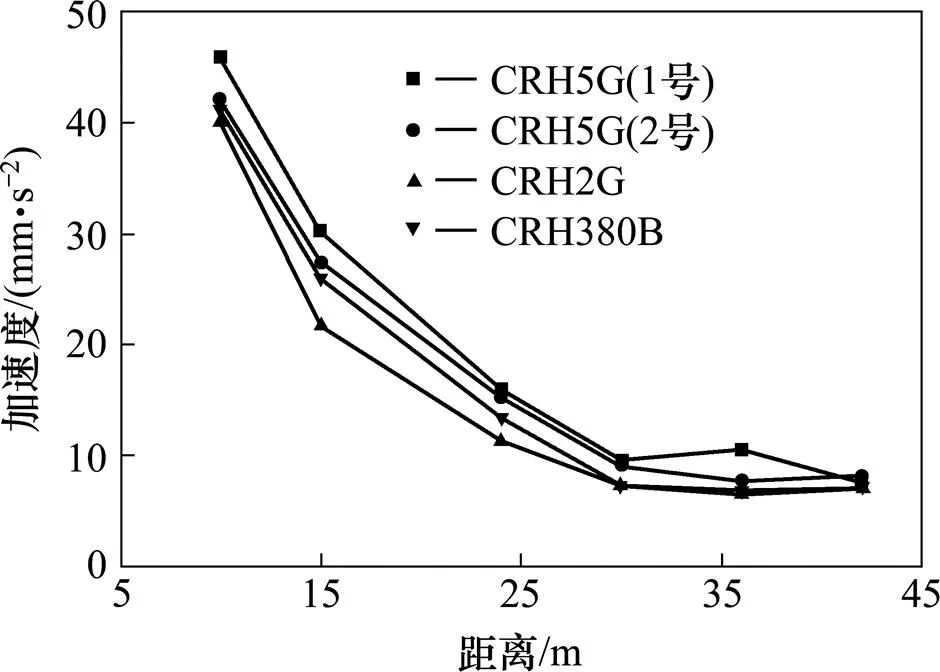
图6 加速度有效值曲线
3 地面振动数值分析
基于现场试验工况,利用多体动力学软件UM建立了车辆模型,同时依据有限元理论[7]建立了轨道−地基模型,考虑车辆—轨道—地基的耦合动力作用,将轨道−地基有限元模型作为子系统导入UM进行耦合计算,从而得到地基在列车动荷载下的动力响应。
如图7所示,轨道振动以振动波的形式传播到地基内部,入射角小于临界角时,地面振动是由入射波在分界面处产生的反射波与直达波的叠加引起的,入射角大于临界角时,还会产生折射波,地面振动受直达波、反射波、折射波共同作用,因此,地面振动与场地速度结构直接相关,而地基速度界面阻抗比、覆盖层厚度是场地速度结构的2个主要方面,同时波阻抗为介质密度和波速的乘积,弹性模量为介质密度与波速平方的乘积,因此不同的模量比对应不同的波阻抗比[8]。基于此,本文依照不同介质模量比,不同覆盖层厚度建立了场地模型,采取数值试验的方法,分析场地不同速度结构对振动反弹的影响。

图7 路堤段振动波传播路径
3.1 模型参数
车辆部分采用CRH5G动车模型,车辆系统参数如表2所示。

表2 车辆系统参数
轨道采用CRTSⅠ型双块式无砟轨道模型,轮轨接触采用FASTSIM轮轨作用模型[9]。轨道参数如表3所示。

表3 轨道参数
以德国低干扰谱[10]的高低不平顺作为激励输入轨道模型,由于列车动荷载下土体变形在弹性变形范围内[11],可以忽略地基土体的非线性,按弹性材料考虑。采用黏弹性人工边界[12]消除有限尺寸区域的边界效应。根据该处地勘资料地基参数取值如表4所示。有限元模型沿线路方向长100 m,车辆−轨道−路基−地基模型示意图如图8所示。

表4 地基模型材料参数

图8 车辆-轨道-路基-地基模型
3.2 数值结果分析
取覆盖层模量为实测值(15.2 MPa),下卧层模量与覆盖层模量之比取1,50,113.8(实际模量比)和200分别进行计算,得到加速度有效值如图9 所示。

图9 不同模量比下振动加速度有效值
如图9所示,实测加速度有效值与模量比为113.8(场地实际模量比)时的数值结果最为接近,表明了模型的合理性与数值计算的正确性。当模量比为1(对应均质情况)时,加速度有效值是随距离单调减小的,并未出现反弹增大现象,模量比分别为50,113.8和200时,10~30 m之间的加速度有效值与均质地基相差不大,而在30~42 m之间出现了反弹增大现象,且模量比越大,反弹的幅度越大,这说明场地速度界面的波阻抗比是形成振动反弹增大和影响其剧烈程度的重要因素。从波的传播理论解释,均质地基模型下,入射波于黏弹性边界处被吸收,直达波在地表传播时,没有反射波和折射波与之叠加,故未出现振动的反弹增大现象,而地基非均质时,入射波于介质分界面处发生反射和折射,与直达波在地表叠加形成振动反弹区,且介质分界面波阻抗比越大,反射波能量越大,故反弹增大幅度也越剧烈。
取覆盖层厚度分别为3,5(实际厚度),7和9 m分别进行计算,得到不同覆盖层厚度下振动加速度有效值如图10所示。
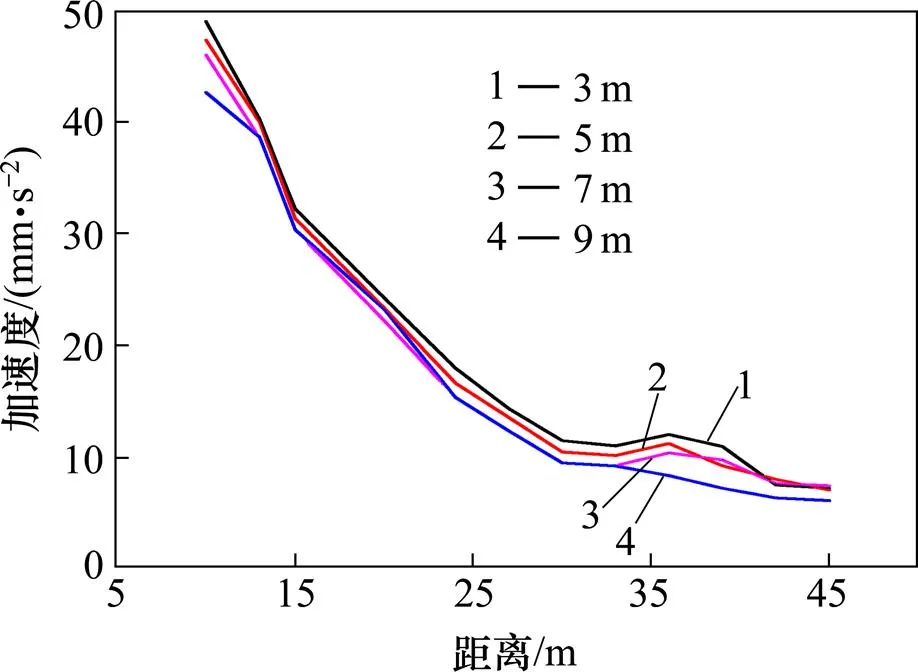
图10 不同覆盖层厚度下振动加速度有效值
图10表明,覆盖层厚度为3~7 m时在距离线路中心线30~42 m处出现的反弹增大现象较显著,随着覆盖层厚度的增大,反弹增大的幅度逐渐减弱,覆盖层厚度为9 m时,没有出现反弹增大现象。可见,覆盖层厚度对振动反弹现象出现与否和剧烈程度也有重要影响。从波的传播理论解释,当覆盖层厚度大到一定程度时,由于介质的阻尼作用,反射波在较长的传播路径上能量已经有很大损耗,与直达波叠加后不足以引起振动的反弹增大。
3.3 列车速度对地面振动的影响
选取了150,200,250和300 km/h4种车速进行计算,分析列车运行速度对地面振动的影响,取实测地基参数,得到不同车速下地面振动峰值加速度如图11所示。

图11 不同车速下地面振动加速度有效值
由图11可以看出,各测点处地面振动在随车速增大呈增大趋势,150 km/h下,加速度随距离衰减较为平缓,随着车速的增加,振动加速度随距离衰减速度也越快。车速为150 km/h和300 km/h时加速度反弹增大在42 m处,200 km/h和250 km/h时加速度反弹增大在36 m处。可见不同车速对振动反弹出现位置也有一定影响。从波的传播理论解释,地面振动可以看作一系列谐波的叠加,车速不同时,引起的地面各频率振动强度不同,不同频率的反射波、折射波的波峰到达地面的位置也不同,故不同车速的振动反弹出现的位置表现出一定的差异。
4 地面振动评价
4.1 评价指标
依据《城市区域环境振动测量方法》(GB 10071—88)[13],地面振动量以振动加速度级来评价。由于各频率成分的振动对人的影响不同,将按《机械振动与冲击——人体暴露于全身振动的评价》(GB/T 13441.1—2007)规定的全身振动k计权因子修正后得到的垂向振动加速度级定义为Z振 级[14],由式(4)得出:

式中:a为经k计权因子修正后的振动加速度有效值,m/s2,0为振动基准加速度有效值,取10−6 m/s2。
由式(4)得出的该处各车型引起Z振级如图12所示。

图12 Z振级
Z振级计算结果表明,Z振级与加速度随距离衰减的规律基本一致,在30~42 m处也出现了反弹增大现象。我国规定铁路干线两侧(铁路外轨两侧30 m外)昼夜间地面振动Z振级不应大于80 dB[13],由图12可以看出30 m外各型列车引起振动的Z振级均小于70 dB,所以该处受高铁地面振动影响是在规范要求之内的。
4.2 Z振级回归分析
对各车型引起Z振级进行回归拟合分析,得到Z振级随距离衰减得回归曲线如图13所示。
可见,各车型引起Z振级随距离的衰减符合对数衰减规律,10~30 m之间拟合效果很好,而在30~42 m之间的反弹增大区拟合效果较差,因此,在对高速铁路引起地面振动进行回归分析时,考虑到反弹增大现象及其影响因素的复杂性,应当将拟合公式的适用范围进行限定,故图12得出的拟合公式适用范围在10~30 m之间。
5 结论
1) 以加速度为指标衡量了CRH5G(1号)车引起各测点的地面振动量。从时域来看,振动加速度随距离增大呈衰减趋势,在10~24m处衰减较快,24~42 m处衰减较慢。从频域来看,10 m处振动加速度主频在100 Hz左右,随着距离的增大,100 Hz高频成分衰减至很小,30~42 m处振动集中25~ 50 Hz。
2) 不同列车引起的地面振动加速度峰值和加速度有效值受列车速度和轴重影响,在距离线路中心线10~36 m处,列车速度越大,引起地面振动加速度越大,而在42 m处,由于振动反弹区的存在,速度较小的CRH5G(2号)引起加速度反而比CRH5G(1号)大。对于同一速度的CRH2G车和CRH380B车,轴重较大的CRH380B引起地面振动加速度较大。
3) 通过数值试验方法对振动反弹分析的结果表明,场地的速度结构是形成和影响振动反弹现象的重要因素,覆盖层与下卧土体模量比、覆盖层厚度对振动反弹的剧烈程度均有影响,这说明在通过数值分析手段研究地面振动时,必须要考虑合理的场地地基结构和参数,否则在振动反弹可能出现的区域得不到准确结果。
4) 对该处的地面振动试验表明其Z振级在距离线路中心线30 m外小于70 dB,没有超出规范限值,回归分析表明Z振级符合对数衰减规律,但在振动反弹区30~42 m处拟合效果较差,说明拟合公式适用范围应当限定在10~30 m之间。
[1] LUO Wei, WANG Ping, YAN Le, et al. Research on the laws of the environmental vibration induced by elevated rail transit[J]. Applied Mechanics and Materials, 2013(405−408): 1881−1886.
[2] FENG Shijin, ZHANG Xiaolei, WANG Lei, et al. In situ experimental study on high speed train induced ground vibrations with the ballast-less track[J]. Soil Dynamics and Earthquake Engineering, 2017(2): 195−214.
[3] 马蒙, 刘维宁, 王文斌. 轨道交通地表振动局部放大现象成因分析[J]. 工程力学, 2013, 30(4): 275−279. MA Meng, LIU Weining, WANG Wenbin. Analysis on the reasons of ground vibration amplification induced by railway traffic[J]. Engineering Mechanics, 2013, 30(4): 275−279.
[4] 郑鑫, 陶夏新, 王福彤, 等.轨道交通地面振动衰减关系中局部放大现象形成机理研究[J]. 振动与冲击, 2014, 33(3): 35−40. ZHENG Xin, TAO Xiaxin, WANG Futong, et al. Mechanism of local amplification in attenuation of ground vibration induced by rail traffic[J]. Journal of Vibration and Shock, 2014, 33(3): 35−40.
[5] Fujikake T. A prediction method for the propagation of ground vibration from railway trains[J]. Journal of Sound and Vibration, 1986, 111(2): 289−297.
[6] GB 10070—88, 城市区域环境振动标准[S]. GB 10070—88, Standard of environmment vibration of urban area[S].
[7] Clouteau D, Degrande G, Lombeart G. Numerical modeling of traffic induced vibration[J]. Meccanica, 2001, 36(4): 401−420.
[8] 廖振鹏.工程波动理论导论[M]. 2版.北京: 科学出版社, 2002: 190−227. LIAO Zhengpeng. Introduction to wave motion theories in engineering[M]. 2nd ed. Beijing: Science Press, 2002: 190−227.
[9] Sajjad Z, Meymand, Alexander Keylin, et al. A survey of wheel–rail contact models for rail vehicles[J]. Vehicle System Dynamics, 2016, 54(3): 386−428.
[10] 翟婉明. 车辆−轨道耦合动力学[M]. 北京: 科学出版社, 2014: 120−125. ZHAI Wanming. Vehicle-track coupled dynamic[M]. Beijing: Science Press, 2014: 120−125.
[11] 夏禾. 交通环境振动工程[M]. 北京: 科学出版社, 2010: 26−28. XIA He. Traffic environment vibration engineering[M]. Beijing: Science Press, 2010: 26−28.
[12] 陈宝魁, 王东升, 成虎. 粘弹性人工边界在地震工程中应用研究综述[J]. 地震研究, 2016, 39(1): 137−142. CHEN Baokui, WANG Dongsheng, CHENG Hu. Research review on the application of viscous-spring artificial boundary in earthquake engineering[J]. Journal of Seismological Research ,2016, 39(1): 137−142.
[13] GB10071—88, 城市区域环境振动测量方法[S]. GB1007—88, Measurement method of environment Vibration of urban area[S].
[14] GB/T 13441.1—2007, 机械振动与冲击人体暴露于全身振动的评价: 第一部分: 一般要求[S]. GB/T 13441.1—2007, Mechanical vibration and shock- evaluation of human exposure to whole-body vibration- part1: General requirements[S].
Experimental study and numerical analysis on ground vibration characteristics of subgrades section of Baoji-Lanzhou high-speed railway
MA Kuikui, LI Bin, WANG Dong, BAI Guangming
(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
Based on the ground vibration problem of ballastless track-subgrade-loess caused by high-speed train dynamic load, the experimental study and numerical analysis in subgrade of Baoji-Lanzhou High-speed Railway were carried out. Combined with experimental data, this paper analyzes the transverse attenuation law of soil vibration acceleration caused by dynamic load of different train, The results show that the attenuation is faster at 10~24 m from the central line of the line. With the increase of the distance, the attenuation speed of 24~42 m from the central line of the line tends to be flat, and the vibration rebound and increase of the ground vibration were caused by each type of vehicle at the distance of 30~42 m are observed. The model of vehicle-track-foundation system was established, and the ground response under the action of train dynamic load was studied. It is found that the model is in good agreement with the measured results, which verifies the rationality of the model and the correctness of the calculation. By changing the modulus ratio of the foundation medium and the thickness of the overburden, the effects of the ratio of the modulus ratio of the foundation medium and the thickness of the overburden on the increase of the vibration rebound are analyzed. The influence of vehicle speed on ground vibration was analyzed. It is found that the ground vibration increases with the increase of speed, and the vibration rebound region caused by different speed trains is different to some extent. According to the Standard of Environmental Vibration in Urban area, the Z vibration level of ground vibration is evaluated. The regression analysis shows that the Z vibration level caused by each type of vehicle conforms to the logarithmic attenuation law, but the fitting effect is poor at 30~42 m in the vibration rebound area. It shows that the applicable range of fitting formula should be limited between 10~30 m.
high-speed railway; ground vibration; field experiment; numerical analysis; vibration rebound
10.19713/j.cnki.43−1423/u.2019.02.003
U211.9
A
1672 − 7029(2019)02 − 0294 − 08
2018−02−24
国家自然科学基金资助项目(51468036)
李斌(1966−),男,甘肃宁县人,教授,从事高速重载轨道结构及轮轨系统动力学研究;E−mail:llbb66@163.com
(编辑 蒋学东)
