高温荷载下CRTSⅡ型板式轨道上拱变形特性研究

赵林，刘学毅，毕澜潇，李京生



高温荷载下CRTSⅡ型板式轨道上拱变形特性研究

赵林1，刘学毅2，毕澜潇2，李京生3

(1. 中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心，北京 100081； 2. 西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031； 3. 中国铁路科学研究院 研究生部，北京 100081)

基于CRTSⅡ型板式轨道在高温荷载作用下的上拱变形是一种比较典型的病害，将功的互等法应用到实际工程中，推导高温荷载作用下弹性薄板的功的互等定理，建立适用于两对边简支两对边自由的轨道板上拱计算模型。分析Ⅱ型板式轨道在温度荷载作用下的上拱变形特性，研究结果表明：在高温荷载作用下轨道板的上拱位移随纵向位置的变化呈正弦曲线变化趋势。分析不同因素对Ⅱ型板式轨道板上拱变形的影响，研究Ⅱ型板式轨道的上拱变形特性。从轨道板垂向稳定性和行车安全性角度，提出优化轨道结构参数和层间病害修补时机的建议。

CRTSⅡ型板式轨道；功的互等定理；高温荷载；轨道板上拱

CRTSⅡ型板式轨道主要由轨道板、砂浆层、支承层等组成[1]，在京沪、京津[2]、沪杭等高铁上广泛使用。高温荷载作用下的上拱变形作为纵连式轨道板的一种典型病害，对轨道系统自身强度和稳定性、对行车的安全性和舒适性均产生不利影响。在列车动荷载、温度及其他环境因素的影响下，CRTSⅡ型板式轨道系统易出现连接处宽窄接缝挤碎和轨道板与砂浆层脱连现象，导致层间整体性降低，在升温荷载和温度梯度荷载的共同作用下，连续轨道板内数以百t计的力对混凝土结构受力和变形产生很大影响，轨道板容易出现上拱变形[3]。现场调研表明[4]，在2013年夏天的高温天气下，多处Ⅱ型轨道板出现了上拱现象(如图1所示)。因此，为了能够进一步优化轨道结构，找出轨道板上拱的原因，研究轨道板上拱变形特性，亟需对高温荷载下CRTSⅡ型板式轨道上拱变形特性的研究提供理论参考。

(a) 层间脱空伤损；(b) 宽窄接缝病害

1 CRTSⅡ型轨道板的互等定理

1.1 CRTSⅡ型板式无砟轨道上拱成因分析

对于连续式轨道结构的CRTSⅡ型板式无砟轨道，主体结构主要由混凝土构件组成，在列车动荷载、温度及其他环境因素的影响下[5]，轨道系统易出现连接处宽窄接缝挤碎和轨道板与砂浆层脱空现象，升温荷载作用下轨道内部将产生巨大的温度压力而造成轨道板上拱[6]。同时，温度梯度荷载在轨道板内部产生温度力矩，加剧了轨道板的上拱变形，并产生层间脱空伤损[7]，CRTSⅡ型板式无砟轨道上拱成因图如图2所示。

1.2 弹性薄板的功的互等定理

无砟轨道以整体性较好的混凝土承载层代替散体的石砟道床，故轨道板在承载能力上可以看作弹性薄板性。应用功的互等法求解弹性薄板弯曲问题具有计算简便，解题过程程序化，并有效地解决特殊荷载的作用和复杂边界条件问题，应用范围广等特点[8]。

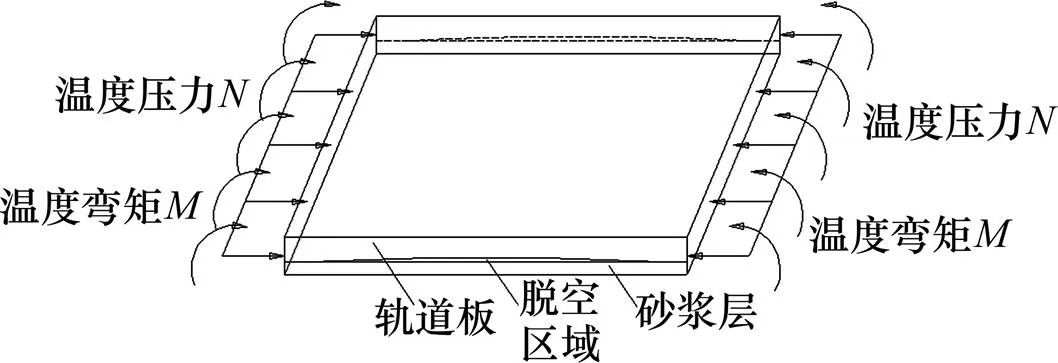
图2 CRTSⅡ型板式无砟轨道上拱成因图

对于都处于真实状态的2个不相同的小变形线性弹性体，2个系统之间有功的互等定理存在[9]：第一弹性体的外力(包括表面力以及边界力)在第二弹性体相应为位移上所做功的总和等于第二弹性体的外力(包括表面力以及边界力)在第一弹性体相应位移上所做功的总和，如式(1)所示。

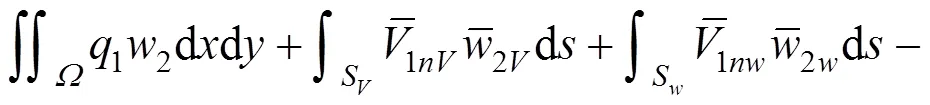
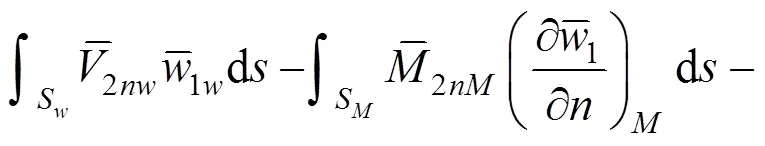
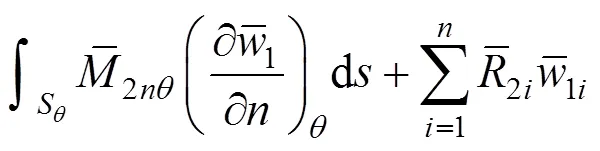
2 CRTSⅡ型板式轨道计算模型及挠曲方程

2.1 CRTSⅡ型板式轨道计算模型

为计算高温荷载作用下CRTSⅡ型轨道板的挠曲方程，将产生砂浆层脱空区域内的轨道板等效为弹性矩形薄板[10]，由于轨道板端部的上拱位移为零，同时在Ⅱ型板的承力结构中宽接缝处不承受弯矩荷载，故一组对边按简支边界处理，另一组对边不受约束，按自由边界条件处理[11]。CRTSⅡ型轨道板在脱空后简化为两对边简支两对边自由的矩形板，不考虑脱空后轨道板与砂浆层的层间作用。计算模型如图3和图4所示。假设弹性薄板所受纵向温度压力和温度弯矩作用于板端形心面，弹性薄板符合小挠度理论假设[12]。

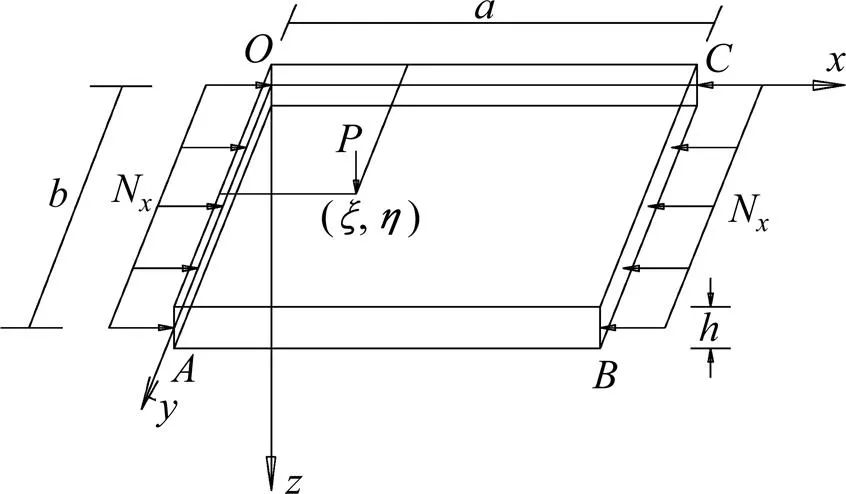
图3 整体升温荷载下的弯曲薄板

图4 温度梯度荷载下的弯曲薄板

2.2 计算参数

CRTSⅡ型轨道板脱连长度为，宽度为，厚度为温度变化Δ=1+，其中1为中性层温度，为温度梯度。则

1) 轨道板纵向温度压力

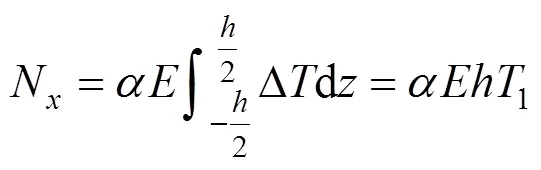
2) 轨道板端部温度弯矩

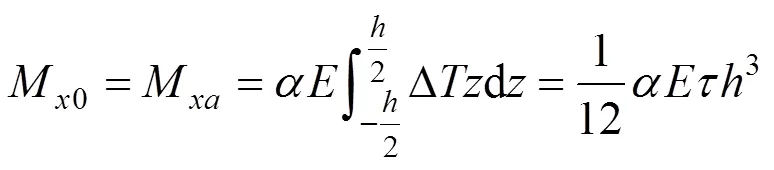
3) 板的抗弯刚度

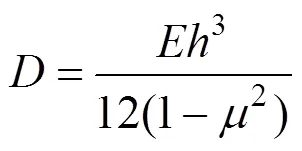
2.3 边界条件

弯曲薄板在=0以及=上板边自由，所有外力均为0，因此有[13]：

1)=0时，

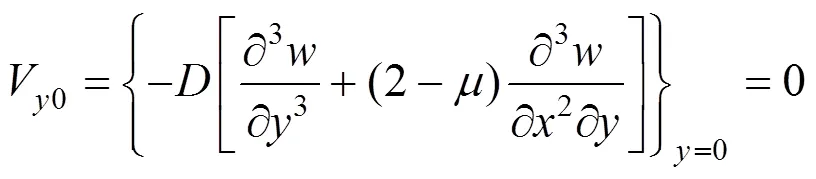
2)=时，

2.4 温度梯度荷载下弯曲薄板的功的互等定理

取在板面流动坐标(,)处受一横向单位集中荷载，同时受纵向温度压力N作用的四边简支矩形薄板为第1系统，如图3所示；而与之受相同纵向温度压力，两对边简支两对边自由，同时端部(简支边)受温度力矩作用的弯曲薄板为第2系统，如图4所示。注意到第1系统的挠曲方程为[14]：

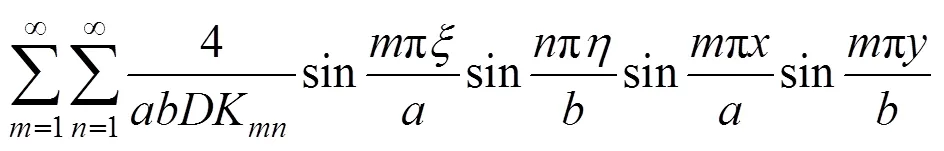
式中：

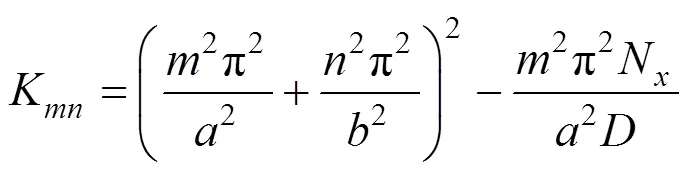
在图3和图4之间应用功的互等定理得：

将挠曲方程式(5)代入式(7)，同时注意到：

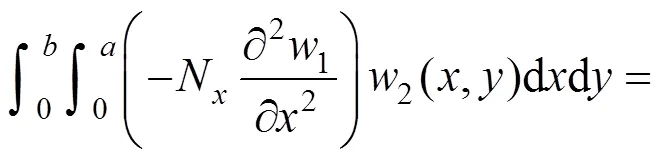
整理得到：

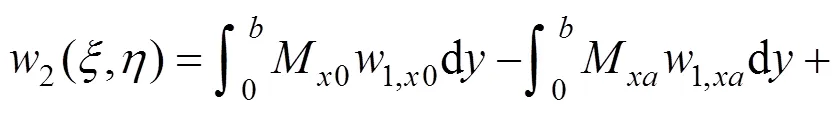
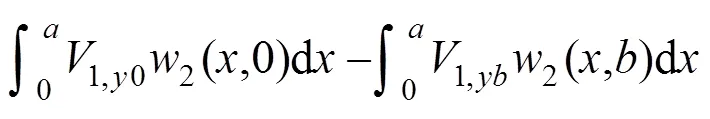
为整理该表达式，做以下假设：

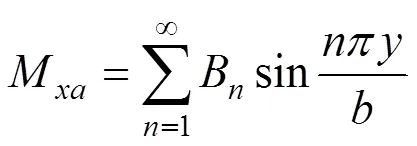
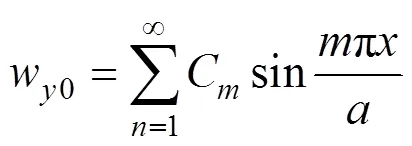
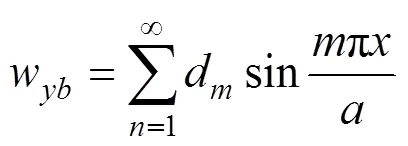
将式(10)~(13)代入式(9)中，同时为避免系统混淆，实际系统的位移以无下标表示，整理后得到双三角无穷级数形式的表达式

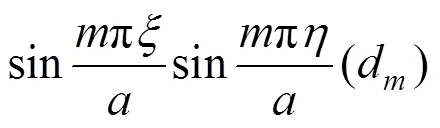
在此表达式中有2个待定未知变量c和d，又弯曲薄板的挠曲函数需满足的边界条件：在=0以及=上板边自由，即

=0 时，

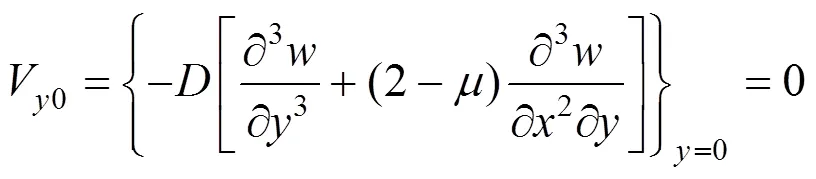
=时，

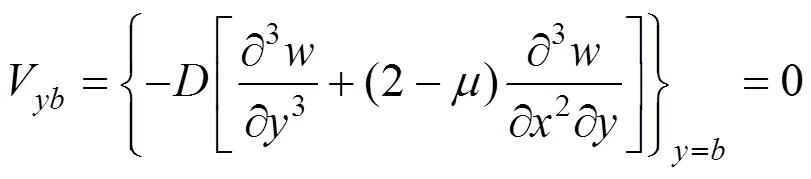
将弯曲薄板位移表达式(14)代入式(15)和式(16)，并根据傅利叶级数性质，对式(15)和式(16)两端用加权余量法[10]进行积分，整理后可得无穷级数非齐次线性方程组：

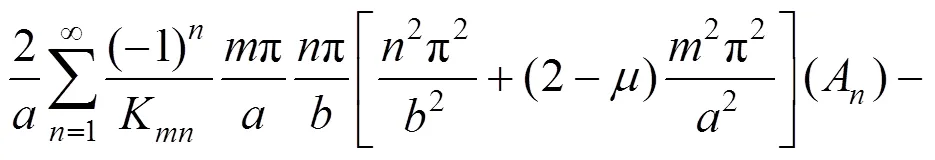
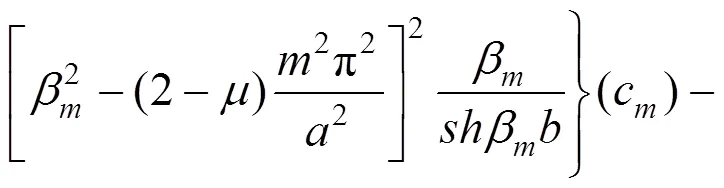
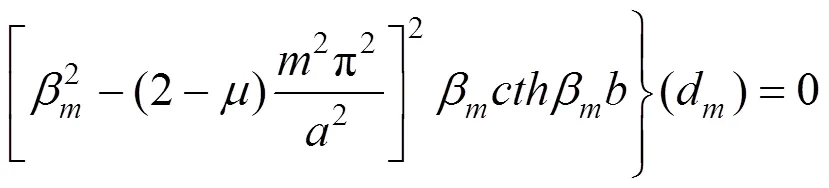
将式(17)及式(18)等价为一非齐次线性方程组，解得

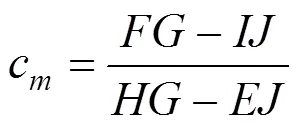
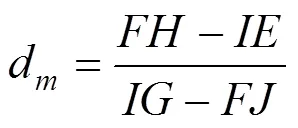
其中：

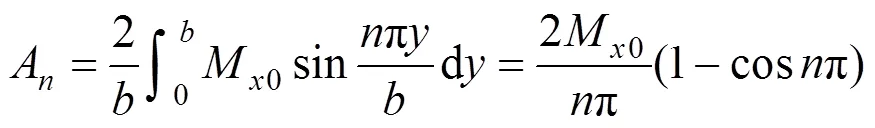
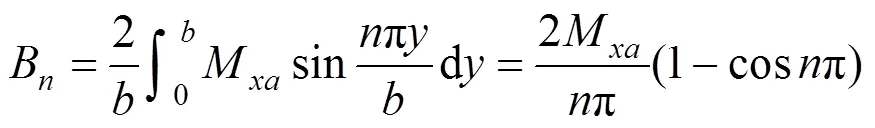
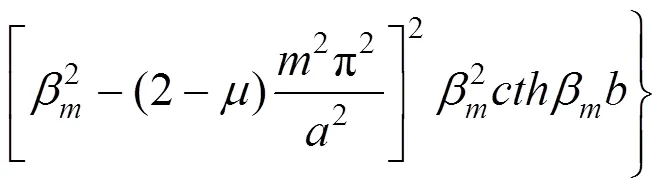
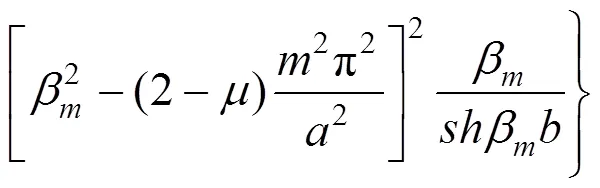
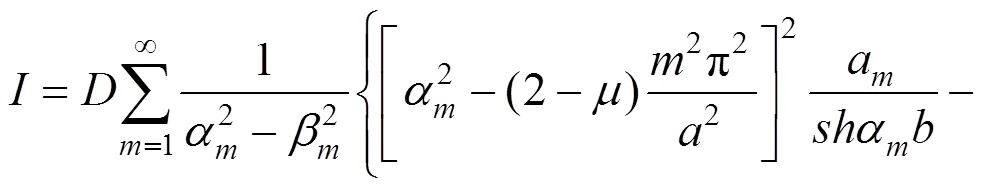
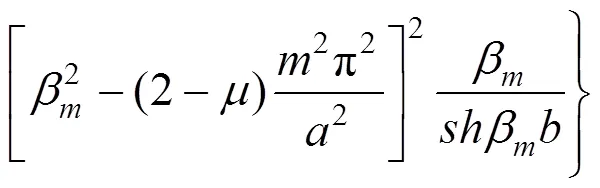
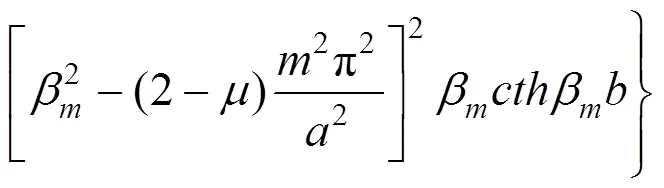
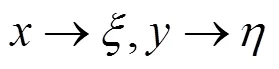
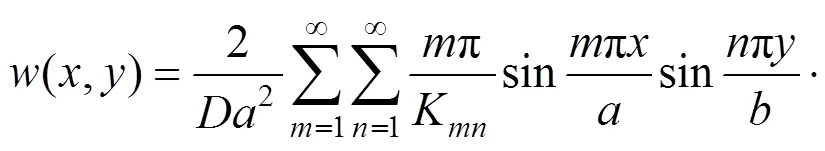
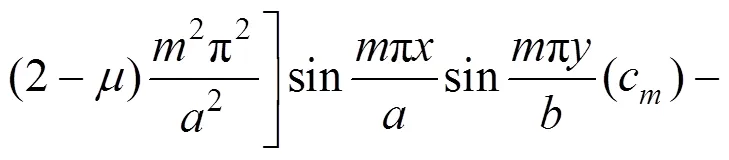
(31)

2.5 案例分析

基于前文推导出的CRTSⅡ型轨道板的挠曲方程，参考沪杭客运专线某简支连续梁桥上CRTSⅡ型板式无砟轨道进行案例分析，轨道板采用C55混凝土。假设轨道板脱空长度为6.45 m(桥上CRTSⅡ型预制轨道板长度)，轨道板所受温度荷载为整体升温为30 ℃，正温度梯度为45 ℃/m，其他主要参数见表1。

表1 桥上CRTSⅡ型板轨道板主要参数

将上述参数代入式(2)~(4)，得到板之抗弯刚度

轨道板纵向温度压力

轨道板端部温度弯矩

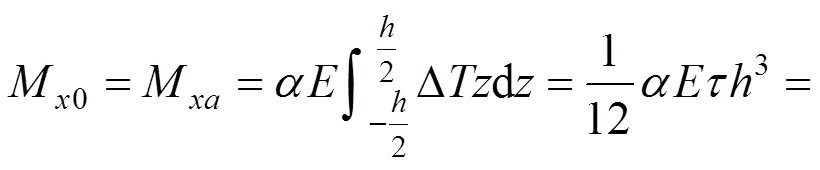
将计算参数代入推导方程式(31)，通过数值分析软件Mathematica编制相应的计算程序得出计算结果。计算结果如图5所示。

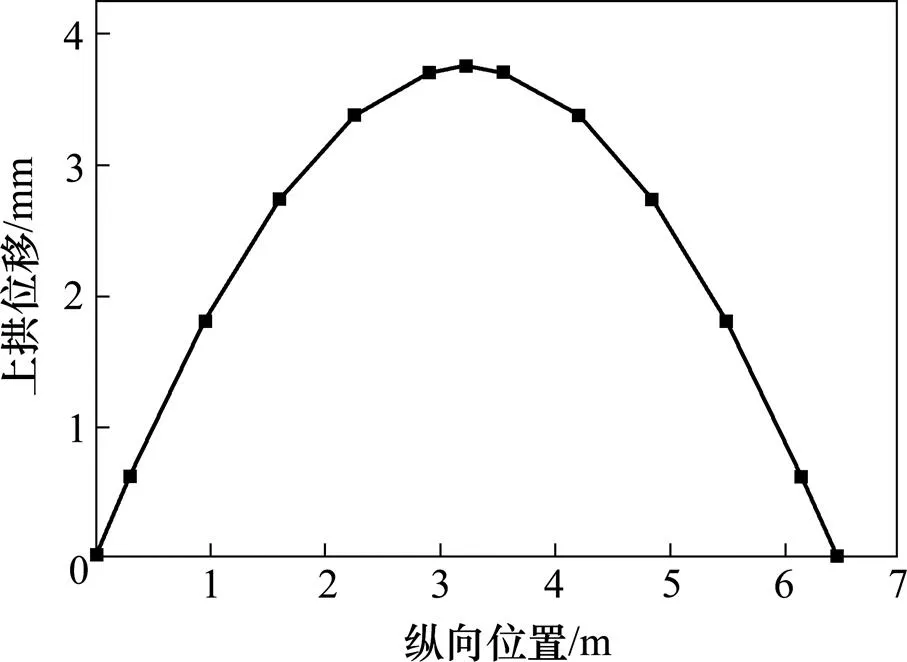
图5 CRTSⅡ型轨道板上拱位移曲线

由图5可知，在整体升温30 ℃和温度梯度45 ℃/m高温荷载共同作用下，随着纵向位置的变化，轨道板的上拱位移先增加后减小，呈现正弦曲线的趋势，半波长6.45 m，轨道板最大上拱位移产生在板中位置，计算数值为3.759 mm。

3 CRTSⅡ型板式轨道上拱变形特性的影响因素研究

对于CRTSⅡ型板式无砟轨道结构，影响轨道板上拱的因素主要有轨道板结构参数、整体升温荷载、温度梯度荷载和脱空长度等。本章基于前文推导出的轨道板挠曲方程，选取桥上Ⅱ型板案例为基本工况，分析不同因素对Ⅱ型板的上拱变形特性的影响。

3.1 轨道板结构参数

3.1.1 轨道板厚度

选取0.18，0.2，0.22，0.24和0.26 m5种轨道板厚度，保持轨道结构其他参数和温度荷载不变，同时在纵向位置依次取了10个扣件位置以及轨道板端部、中部共13个观测点，研究轨道板厚度对轨道板的上拱位移影响。计算结果如图6所示。

如图6(a)所示趋势可知，在脱空长度不变的情况下，轨道板的上拱变形仍然呈现正弦曲线的变化规律，半波长6.45 m，轨道板最大上拱位移产生在板中部；对比图6(b)可知，随着轨道板厚度的不断增加，轨道板上拱位移越来越小，而且直线的斜率越来越小，这是由于随着厚度的增加，板之抗弯刚度成三次方的倍数增长，这导致轨道板的最大上拱位移减小的越来越缓慢，最大上拱位移分别为4.391，3.759，3.395，3.161和3.001 mm。因此，在保证轨道结构受力满足要求的基础上，适当地增大轨道板厚度有助于减小温度荷载引起的轨道板上拱。

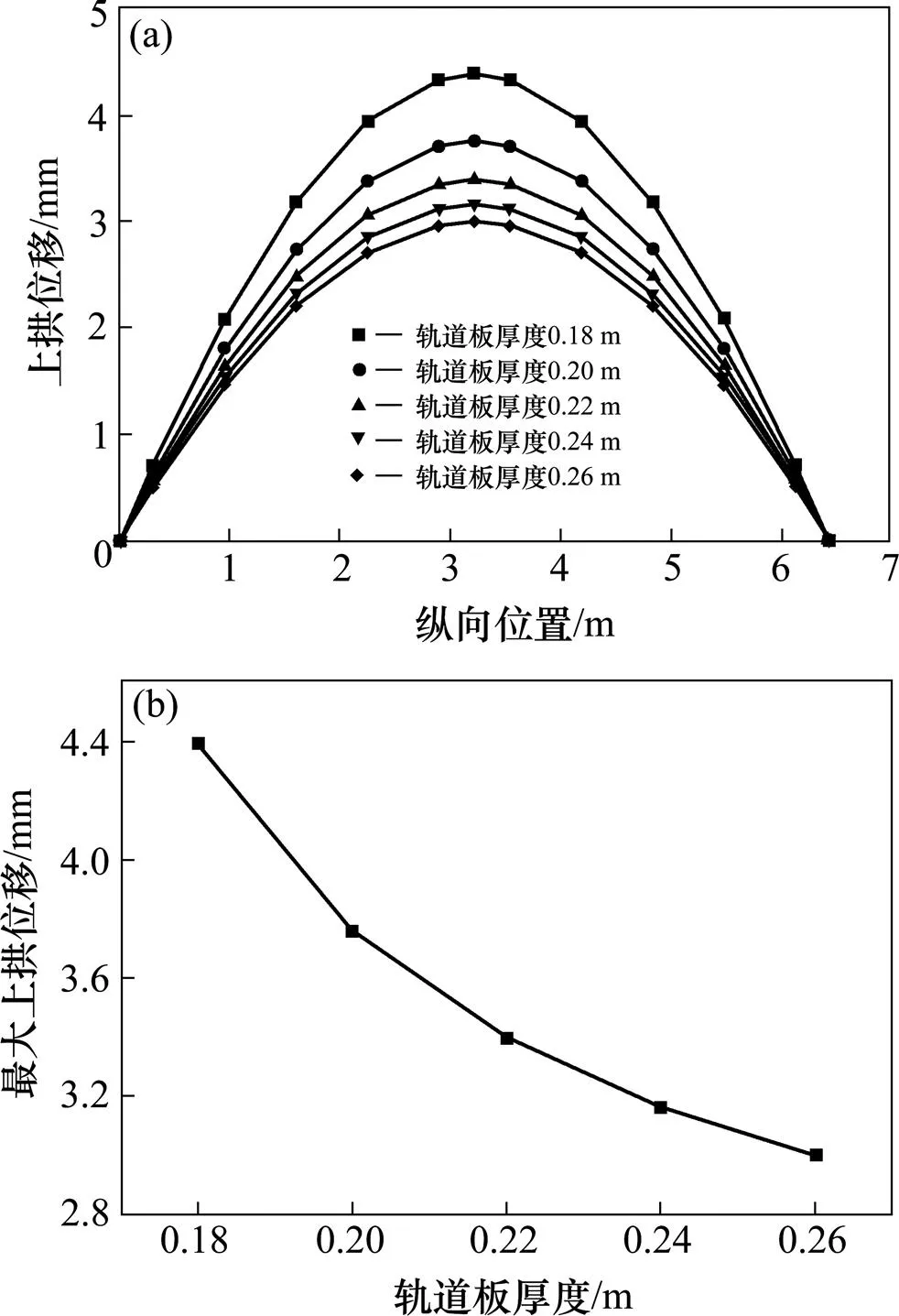
(a) 轨道板上拱位移；(b) 轨道板最大上拱位移

3.1.2 轨道板厚度

选取2，2.2，2.55，2.8和3.0 m5种轨道板宽度，保持轨道结构其他参数和温度荷载不变，同时在纵向位置依次取了10个扣件位置以及轨道板端部、中部共13个观测点，研究轨道板宽度对轨道板的上拱位移影响。计算结果如图7所示。

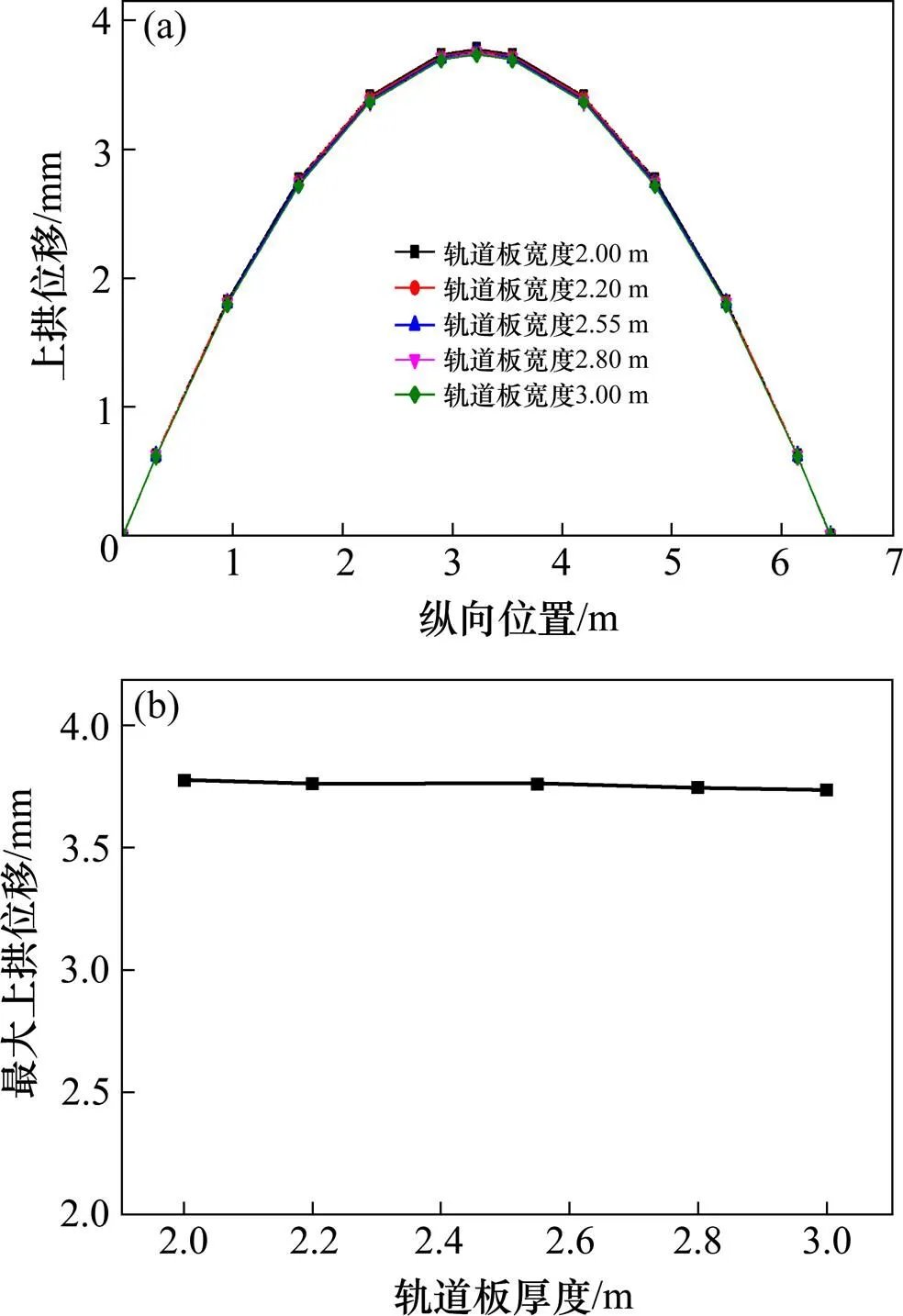
(a) 轨道板上拱位移；(b) 轨道板最大上拱位移

对比图7(a)和图7(b)，我们发现随着轨道板宽度的增加，轨道板的上拱位移变化有限，轨道板的最大上拱位移几乎不变，分别为3.776，3.762，3.759，3.746和3.736 mm，变化率分别为0.37%，0.18%，0.32%和0.26%，并且轨道板上拱变形所呈现的正弦曲线变化规律不变，半波长6.45 m，可见轨道板宽度对轨道板上拱变形的影响很小。因此，在保证轨道结构受力满足要求的基础上，出于减少材料用料，施工方便，节约预算的角度考虑，可以适当的减少轨道板宽度。

3.2 整体升温

选取20，30，40和50 ℃ 4种整体升温工况，保持轨道结构参数不变，在纵向位置依次取了10个扣件位置以及轨道板端部、中部共13个观测点，研究整体升温对轨道板的上拱位移影响。计算结果如图8所示。

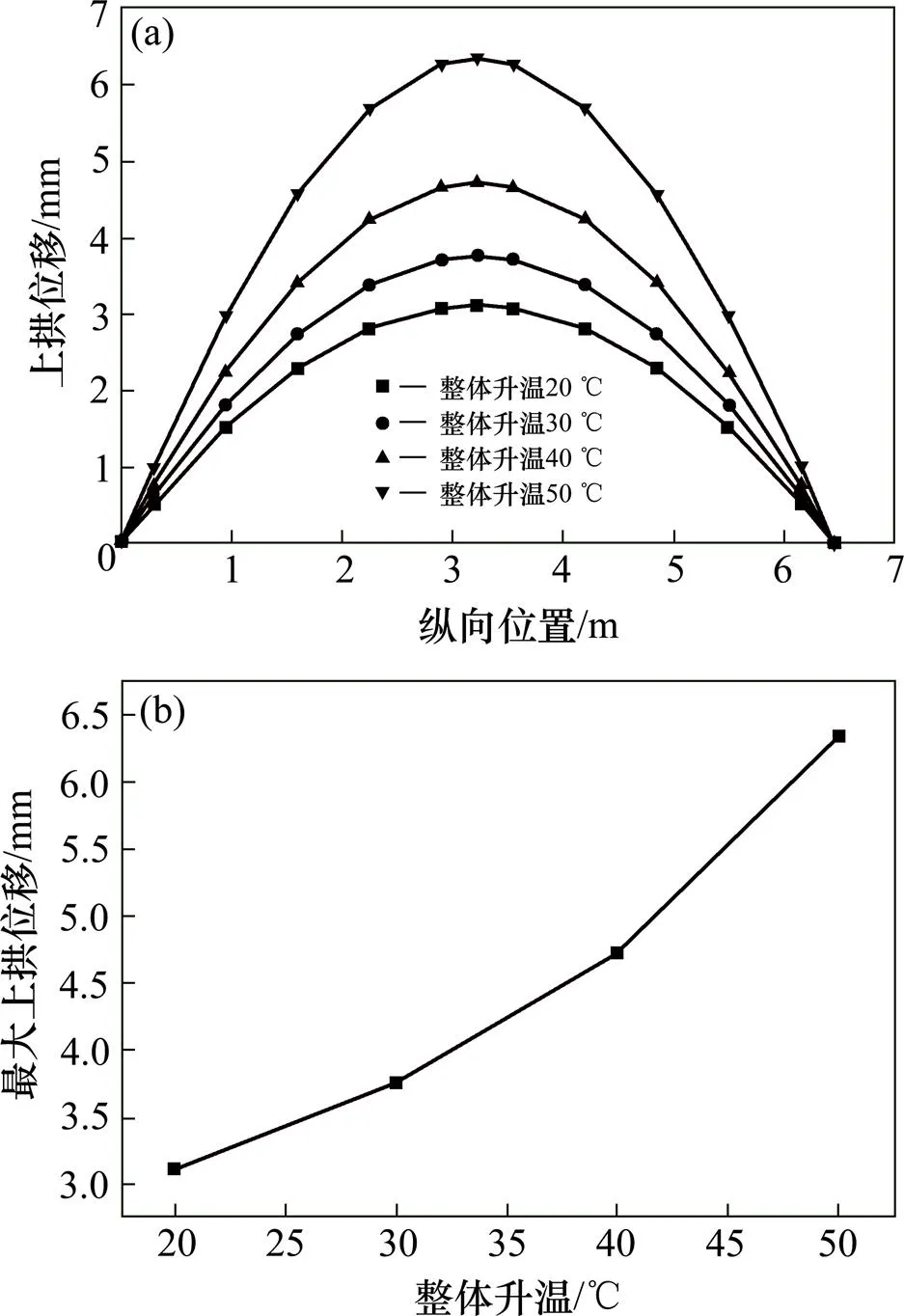
(a) 轨道板上拱位移；(b) 轨道板最大上拱位移

图8(a)所示可知，整体升温的变化没有改变轨道板上拱变形的正弦趋势；对比图8(b)，随着整体升温的不断增加，轨道板的上拱位移越来越大，并且直线的斜率越来越大，表明轨道板的上拱变形对整体升温荷载作用很敏感，这是由于温度梯度的作用下轨道板有一个初始挠曲变形，而随着整体升温的增加，板端所受纵向压力不断加剧，导致轨道板的上拱位移不断增加，最大上拱位移分别为3.116，3.759，4.724和6.344mm，可见当整体升温达50 ℃时，最大上拱位移已达到6.344mm，根据《高速铁路无砟轨道线路维修规则(最终稿)》[11]中规定，此时最大上拱位移比较接近轨道板的最大允许上拱度8 mm，将威胁到行车的安全性和平稳性。因此，建议在气温较高的夏季，应加强轨道板上拱位移的监测。

3.3 温度梯度

选取25，35，45，55和65 ℃/m 5种温度梯度工况，保持轨道结构参数不变，在纵向位置依次取了10个扣件位置以及轨道板端部、中部共13个观测点，研究温度梯度对轨道板的上拱位移影响。计算结果如图9所示。

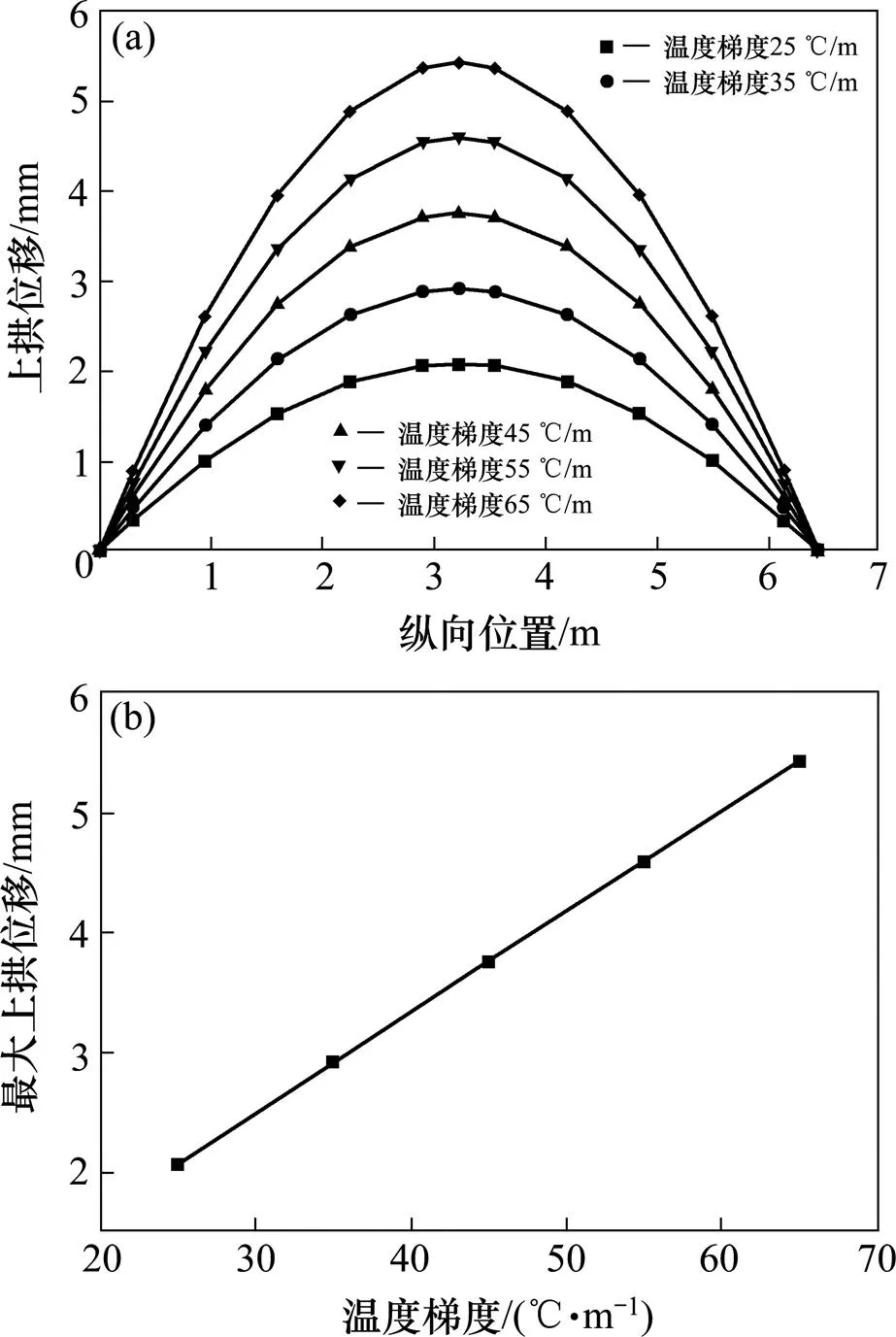
(a) 轨道板上拱位移；(b) 轨道板最大上拱位移

由图9(a)所示可知，随着温度梯度的变化，轨道板上拱位移仍然保持正弦曲线的趋势；对比图9(b)可知，随着温度梯度的不断增加，轨道板的上拱位移呈线性增加，这是由于温度梯度的增加使端部所受温度弯矩增加，而纵向压力不变，轨道板上拱位移与温度弯矩呈一次线性关系。轨道板最大上拱位移分别为2.073，2.923，3.759，4.593和5.428 mm，可以预测在极端天气下当正温度梯度为85 ℃/m时，轨道板最大上拱位移将达到7.8 mm，根据《高速铁路无砟轨道线路维修规则(最终稿)》[15]中规定，此时最大上拱位移接近轨道板的最大允许上拱度8 mm，将威胁到行车的安全性和平稳性。因此，建议在太阳辐射较强的地区和气候，应加强轨道板上拱位移的监测。

3.4 脱空长度

选取1.6，3.2，4.8和6.45 m4种脱空长度的工况，在纵向位置依次选取11~13个不等的观测点，以尽可能反应轨道板的上拱变形特性，研究脱空长度对轨道板的上拱位移影响。计算结果如图10 所示。

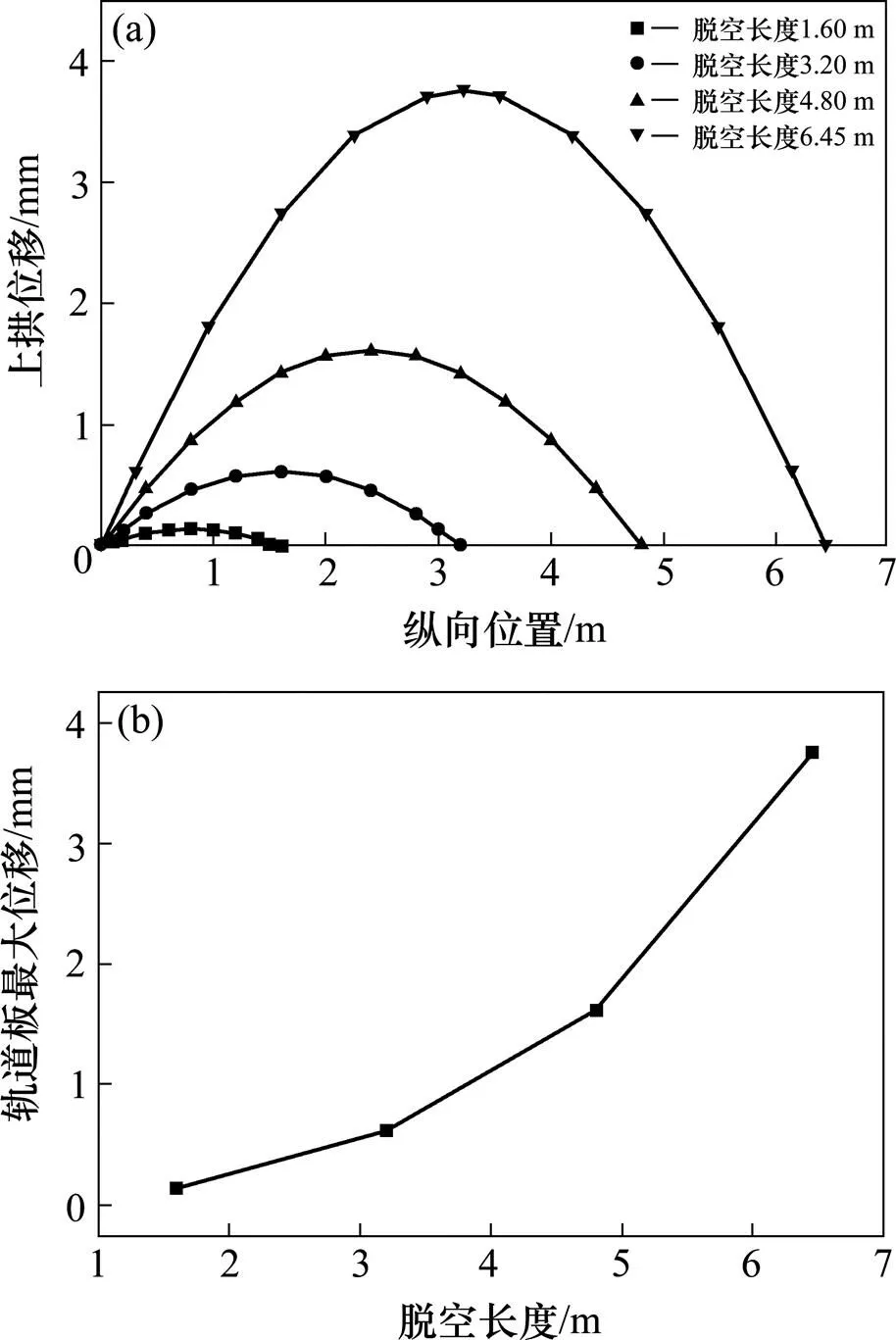
(a) 轨道板上拱位移；(b) 轨道板最大上拱位移

由图10(a)所示可知，随着脱空长度的增长，轨道板上拱位移的正弦曲线半波长也不断增加，分别为1.6，3.2，4.8和6.45 m；对比图10(b)可知，随着脱空长度的不断增加，轨道板的上拱位移加快增长，直线的斜率越来越大，最大上拱位移分别为0.141，0.615，1.615和3.759 mm，依次增加了3.36倍、10.45倍和25.66倍，可见脱空长度对轨道板上拱变形影响较大，这是由于脱空长度的增加使轨道板上拱的临界弦长增加，降低了轨道板失稳的临界荷载，而在端部温度弯矩和纵向压力不变的情况下，其上拱变形必然增大。因此在实际工程中，应重视层间伤损的演变，对于出现的层间病害应及时维修和修补；此外轨道板的上拱变形也将加重层间病害，对轨道结构受力产生不利影响。

4 结论

1) 将功的互等法应用到实际工程中，推导了高温荷载作用下弹性薄板的功的互等定理，建立了适用于两对边简支两对边自由的轨道板上拱的计算模型。

2) 以CRTS Ⅱ型板式无砟轨道在高温荷载作用下上拱变形为研究对象，建立了高温荷载下轨道板的功的互等定理，推导出CRTS Ⅱ型轨道板的挠曲方程。分析了CRTS Ⅱ型板式轨道在高温荷载作用下的上拱变形特性，结果表明在整体升温和温度梯度荷载共同作用下的轨道板的上拱变形随纵向位置的变化呈正弦曲线变化趋势，半波长即为轨道板脱空长度，轨道板最大上拱位移产生在板中 位置。

3) 轨道板厚度对其上拱位移影响较大，在保证轨道结构受力满足要求的基础上，适当增大轨道板厚度有助于减小高温荷载引起的轨道板上拱。轨道板宽度对其上拱位移影响十分有限，在保证轨道结构受力满足要求的基础上，出于减少材料用料，施工方便，节约预算的角度考虑，可以适当减少轨道板宽度。

4) 整体升温和温度梯度荷载对轨道板上拱位移影响较大，建议在气温较高的夏季以及太阳辐射较强的地区和气候，应加强轨道板上拱位移的 监测。

5) 随着轨道板脱空长度的增加，轨道板上拱位移的正弦曲线半波长不断增加，轨道板的上拱位移增加明显，在实际工程中，应重视层间伤损的演变，对于出现的层间病害应及时维修和修补。

[1] 杨荣山. 轨道工程[M]. 北京: 人民交通出版社, 2013. YANG Rongshan. Track engineering[M]. Beijing: China Communications Press, 2013.

[2] HE H W, HOU W W. Development of ballastless track technology on China railway (CR)[J]. RTR, 2006(Suppl): 18−22.

[3] 李培刚. CRTSⅡ型板式轨道层间损伤及其影响研究[D].成都: 西南交通大学, 2015. LI Peigang. Analysis of the Interface damage of CRTS II slab track and its influences[D]. Chengdu: Southwest Jiaotong University, 2015

[4] 曾毅. 纵连式轨道板垂向稳定性研究[D].成都: 西南交通大学, 2014. ZENG Yi. Research on vertical stability of the longitudinal coupled slab track[D]. Chengdu: Southwest Jiaotong University, 2014

[5] 王继军, 尤瑞林. 单元板式无砟轨道结构轨道板温度翘曲变形研究[J]. 中国铁道科学, 2010, 31(3): 9−14. WANG Jijun, YOU Ruilin. Research on the slab temperature warping of the unit slab track system[J]. China Railway Science, 2010, 31(3): 9−14.

[6] Eisenmann J. Dimensionierung einer festen fahrbahn[J]. Eisenbahnin-genieur, 1991, 42(3): 116−118.

[7] 林红松, 刘学毅, 杨荣山.大跨桥上纵连板式轨道受压稳定性[J]. 西南交通大学学报, 2008, 43(5): 673−678. LIN Hongsong, LIU Xueyi, YANG Rongshan. Compressive stability of continuous slab-track on long-span bridge[J]. Journal of Southwest Jiaotong University, 2008, 43(5): 673−678.

[8] 付宝连. 功的互等理论及其应用[M]. 北京: 国防工业出版社, 2007. FU Baolian. Reciprocal theory of works and its applications[M]. Beijing: National Defense Industry Press, 2007.

[9] Timoshenko S P. Theory of elastic stability[M]. 2nd ed. McGraw-Hill, 1961: 35−70.

[10] 黄与宏. 板结构[M]. 北京: 人民交通出版社, 1992. HUANG Yuhong. Plate structure[M]. Beijing: China Communications Press, 1992.

[11] 何福保, 沈亚鹏. 板壳理论[M]. 西安: 西安交通大学出版社, 1993. HE Fubao, SHENG Yapeng. Theory of plate and shell[M]. Xi’an: Xi’an Jiaotong University Press, 1993.

[12] 付宝连. 弯曲薄板功的互等新理论[M]. 北京: 科学出版社, 1993. FU Baolian. The new reciprocal theorem of works of curved plate[M]. Beijing: Science Press, 1993.

[13] 付宝连. 有限变形非线性弹性力学的倒易定理[J]. 燕山大学学报, 2002, 23(6): 188−194. FU Baolian. Reciprocal theorem for non-linear elasticity with finite displacements[J]. Journal of Yanshan University, 2002, 23(6): 188−194.

[14] 朱敬举. 弹性矩形薄板稳定问题的广义位移解及应用[D]. 秦皇岛: 燕山大学, 2001. ZHU Jingju. Generalized displacement solution for elastic stability of thin rectangular plates and its application[D]. Qinhuangdao: Yanshan University, 2001.

[15] 中华人民共和国铁道部. 高速铁路无砟轨道线路维修规则(最终稿)[S]. Ministry of Railways of the People’s Republic of China.High-speed railway ballastless track repair rules (final draft)[S].

Study on upwarp deformation characteristics of CRTS II prefrabricated track slab under high temperature load

ZHAO Lin1, LIU Xueyi2, BI Lanxiao2, LI Jingsheng3

(1. Railway Science & Technology Research & Development Center, China Academy of Railway Science Corporation Limited, Beijing 100081, China; 2. Key Laboratory of High-Speed Railway Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China; 3. Postgraduate Department, China Academy of Railway Sciences, Beijing 100081, China)

Upwarp deformation of CRTS II prefabricated track slab under high temperature load is a kind of typical diseases. Reciprocal theorem method was applied to practical engineering, and reciprocal work theorem of elastic thin slab under high temperature load was derived. The calculation model which is applied to two opposite sides simple support and free structure track slab upwarp was estalished. Upwarp deformation characteristics of CRTS II prefrabricated track slab under temperature load were analyzed. The results of study show that upwarp displacement of track slab presented a trend of sine curve along with the change of vertical position under high temperature load. The influence of different factors on upwarp deformation of CRTS II prefrabricated track slab are analyzed, and upwarp deformation characteristics of CRTS II prefrabricated track slab are studied profoundly. From the perspective of track slab vertical stability and driving safety, the advice of interlayer diseases repairing and optimization of track structure parameters are proposed tentatively.

CRTS II prefrabricated slab track; reciprocal theorem method; high temperature load; track slab upwarp

10.19713/j.cnki.43−1423/u.2019.02.001

U213.244

A

1672 − 7029(2019)02 − 0277 − 10

2017−10−25

高铁联合自然基金资助项目(U1424208)；中国铁道科学研究院资助项目(2016YJ141，2017YJ141)

刘学毅(1962−)，男，四川中江人，教授，博士，从事高速、重载轨道结构与轨道动力学的研究；E−mail：xyliv@home.swjtu.edu.cn

(编辑 蒋学东)