基于有限元极限上限法的含软弱夹层边坡稳定性分析
2019-03-07皮晓清李亮唐高朋张锐赵炼恒
皮晓清,李亮,唐高朋,张锐,赵炼恒
基于有限元极限上限法的含软弱夹层边坡稳定性分析
皮晓清,李亮,唐高朋,张锐,赵炼恒
(中南大学 土木工程学院,湖南 长沙 410075)
由于软弱夹层的存在通常会使得边坡更易发生失稳破坏,通过引入考虑强度折减法的有限元极限分析上限法,构建含软弱夹层边坡稳定性分析的非线性规划模型,并采用可行弧内点算法与网格自适应方法进行优化求解,获得不同软弱夹层的厚度、倾角、深度以及软弱夹层与周围土体的相对强度影响下的边坡安全系数及破坏模式。研究结果表明:软弱夹层的厚度、倾角、深度以及相对强度对边坡安全系数及滑裂面位置的影响显著;但当软弱夹层的深度和相对强度增大到一定值时,边坡稳定性不再受其影响。本文结果与已有文献的结果吻合较好。
边坡稳定性分析;软弱夹层;极限分析上限法;安全系数
软弱夹层是岩体中的不连续面,由于其物理力学性质差,不论厚薄,都会给工程建设带来一系列问题,常成为地下洞室、边坡稳定、坝基和坝肩抗滑稳定等的控制性弱面[1]。边坡中的软弱夹层也是造成实际滑坡的主要因素之一[2−5]。因此,对含软弱夹层边坡的变形机理、破坏特征及稳定性展开研究具有重要的现实意义。目前含软弱夹层边坡稳定性分析方法主要有:极限平衡法[4−5],弹−塑性有限元法[4, 6]和极限分析法[8−13]等。其中极限分析方法,由于其明确的物理意义和严格的解答范围[7],在边坡稳定性分析方面得到了广泛的应用[2−13]。它的引入为含软弱夹层边坡稳定性分析提供了较为严密的理论依据,传统极限分析方法采用组合机构来构建软弱夹层边坡破坏模型,这往往需要对组合破坏模式进行假定[9−10],由于含软弱夹层边坡破坏的复杂性,常造成破坏模型的假定不完全符合实际情况。有限元极限分析方法可以弥补上述方法的不足。其优势在于,极限分析方法的引入为边坡稳定性分析提供了严密的理论基础;采用有限元的形式,便于控制计算域内强度参数及外部荷载的分布形式,使得非均质材料,复杂荷载条件和几何构造下的边坡稳定问题研究更加简便[14]。对于含软弱夹层边坡,刘小丽等[8]提出一种用于含软弱夹层边坡降雨入渗稳定性极限分析上限法;黄茂松等[9]采用极限分析上限法,基于转动−平动组合破坏机构,进行含软弱夹层边坡的稳定性分析;汤祖平等[13]提出改进的转动−平动组合破坏机构和便于工程应用的直线滑动破坏机构进行稳定性研究。上述文献均是研究简单含单一软弱薄夹层稳定性上限分析,但是在破坏模式中假设软弱薄层为一条直线,没有考虑软弱夹层厚度的影响。另外对含软弱夹层边坡稳定性分析时也未考虑软弱夹层的倾角、其与土体相对强度以及厚度的对边坡稳定性的影响。基于以上原因,本文在文献[15]的基础上引入强度折减技术,以获得通用的安全系数来对含软弱夹层边坡稳定性进行评估分析,对比以往的经典案例,来验证其有效性和适用性。进一步以含单一软弱夹层边坡为例,探讨软弱夹层的厚度,倾角及其与土体相对强度与深度变化对边坡安全系数及滑裂面位置的影响规律。以期拓展该方法在含软弱夹层边坡稳定性分析领域的应用。
1 含软弱夹层边坡稳定的上限法数学模型构建简介
边坡稳定的上限法数学规划模型是通过有限元上限分析法将寻找机动相容速度场问题转化为相应数学规划问题,并通过计算机自动搜索复杂条件下的速度场。其基本思路为:引入速度间断线对边坡进行三角形单元离散,以单元节点位移速度为未知量,根据上限定理相关的约束条件和待优化的边坡稳定目标函数,可建立相应的边坡稳定的上限法数学规划模型。最后,采用适当的数学规划算法进行求解,获得目标函数的最优解答。由于篇幅限制,相关网格划分、优化计算和程序实现部分内容可参考文献[15−19],以下仅对含软弱夹层边坡模型构建,强度折减技术的引入进行说明。
1.1 含软弱夹层边坡数值模型的构建
本文采用含单一软弱夹层边坡的模型,其计算网格划分以及边界条件,如图1所示。
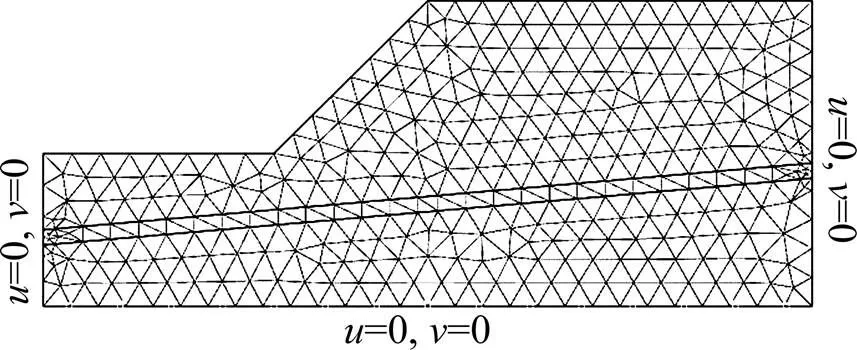
图1 有限元上限法计算网格和边界条件
其中:和分别代表水平和竖直方向,边界约束条件是:左右两侧以及下侧边界在水平和竖直方向速度均为0,其余临空面均为自由界面。含软弱夹层边坡各区域土体为均质各向同性理想弹塑性材料,服从Mohr-Coulomb屈服准则。对不同网格计算区域赋予不同的强度参数来表征土体和软弱夹层特性。特别地,对于平面应变问题,摩尔库伦破坏准则难以满足连续光滑的要求,因此,本文采用双曲线型近似摩尔库伦破坏准则,详见文献[20]。
1.2 强度折减技术的引入
已有的有限元极限分析法中往往是通过对土体内重力荷载或者外荷载进行优化获得荷载因子 (超载系数0)来体现边坡的安全储备,未能给出通用的安全系数(F)。基于此,本文在已有研究基础上,引入强度折减技术实现对土体强度参数的折减,以获得边坡极限状态下的安全系数,其求解思路类似于参考文献[14]和[18]。其流程图如图2所示。

图2 安全系数计算流程图
首先设置一个初始安全系数s0=1,用折减后的剪切强度参数c0和φ0替代初始的和,然后进行优化求解获得UB0以及对应的超载系数0=UB0/,其中,UB0为优化后的土体自重,为土体实际自重。倘若01.0,令Δs=−(可根据实际情况进行调整,一般设置为0.1),反之则令Δs=;此时得到更新的s1=s0+Δs,再进行折减得新的折减后剪切强度参数c1和φ1替代原有c0和φ0,然后进行优化求解获得UB1以及对应的超载系数1=UB1/。倘若(0−1)(1−1)>0,则令01,s0=s1,重复计算。直至(0−1)(1−1)<0,此时,最终的安全系数s可通过线性插值获得为:s=s0+(s1−s0) (0−1)/(0−1)。
2 含软弱夹层边坡对比计算与分析
图3为含软弱夹层边坡,其计算范围和边界条件与文献[9]完全相同,其中各土层材料的强度参数如表1给示。
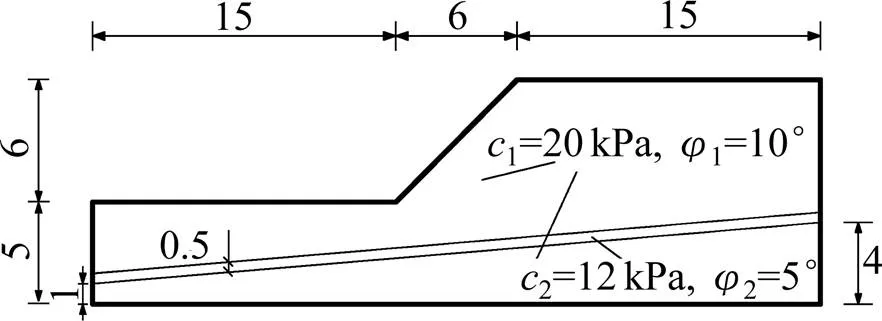
单位:m

表1 各土层土体材料参数
经优化求解得使边坡的安全系数s为1.267,将获得的计算结果导入tecplot360分别得边坡处于极限状态时的自适应网格分布图,能量耗散分布图以及速度场分布图,如图4~6所示。

图4 含软弱夹层边坡网格自适应分布图

图5 含软弱夹层边坡能量耗散分布图

图6 含软弱夹层边坡速度场分布图
由图4~6可知,本方法获得的网格加密区与速度场及塑性能耗变化较大的区域保持一致。由图6可知,边坡的滑动面贯穿边坡的软弱夹层,并与软弱夹层下方土体相切,从离坡趾不远处地面滑出。不同方法下的安全系数研究结果对比如表2所示,不同方法下获得的滑裂面对比如图7所示。

表2 不同方法下边坡安全系数Fs对比

图7 临界滑裂面对比图
由表2可以看出,本文所得到的安全系数与其他3种方法得到的计算结果较为接近,最大相对误差不超过2.3%,因此运用本文方法来分析含软弱夹层边坡稳定性是有效的。由图7看出,本文方法获得的滑动面与有限元获得滑动面十分接近,且均穿过软弱夹层,而黄茂松等[9]获得的滑裂面与软弱夹层相切,未能通过软弱夹层。然而,以上3种方法获得的安全系数几乎一致,原因可能在于,本算例中的软弱夹层土体的厚度较小,贯穿或相切对边坡的稳定性微小。
青海省海西州德令哈市民族学校的索卫华对海西地区民族中学学生数学学习中导致数学基础较差的社会环境、家庭教育、教师的知识面及传授方法等智力和非智力因素进行了剖析.中央民族大学苏傲雪对全国31所内地新疆高中班学校的932名教师和1 873名学生进行了问卷调查和测试,对影响内地新疆班学生数学学业成绩的因素作了统计分析.云南曲靖师范学院孙雪梅综合应用调查测试、作业分析、口头报告和比较研究方法,从表征视角调查了七年级彝族学生数学学习现状,发现七年级彝族学生在解决数学问题上的数学表征水平发展不均衡,而七年级彝族学生与同年级汉族及其他少数民族学生没有显著差异.
3 含软弱夹层边坡稳定性参数分析
为进一步揭示含软弱夹层土体边坡的失稳破坏机制及稳定性特征,本节以单层软弱夹层边坡为例,探讨软弱夹层的厚度、倾角、其与土体相对强度以及深度变化对边坡安全系数及滑裂面位置的影响规律,揭示其失稳破坏机制及稳定性特征。结合已有研究成果[4],其模型的边界条件设置如图8所示。
其中,为边坡的坡角,为边坡的高度,为软弱夹层的倾角,软弱夹层的厚度。左边界高度为,右边界高度为2,左边界至坡脚的距离为1.5,坡顶至右边界的距离为2.5,软弱夹层上界面至左边界的距离为0.5。
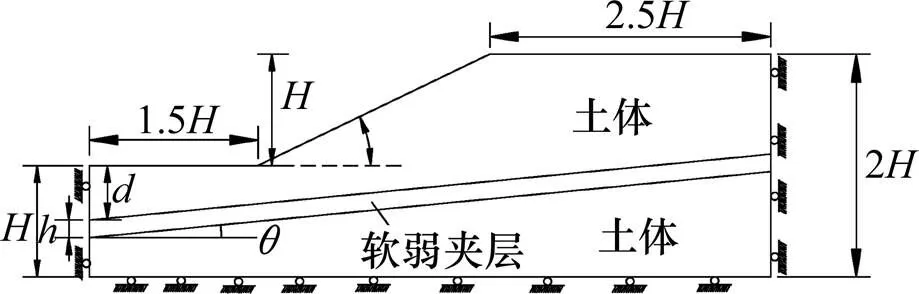
图8 计算模型与参数
3.1 软弱夹层厚度对边坡稳定性的影响
令模型坡高=10 m,边坡的角度=45°,软弱夹层的倾角=5°,软弱夹层上界面深度/=0.5,软弱夹层的厚度/=0.05~0.4,土体强度参数1=20 kPa,1=20°,软弱夹层与土体的相对强度2/1=2/1=0.25,其中土体自重均为=20 kN/m3。经计算求解可得不同软弱夹层的厚度下边坡安全系数及其相应的能量耗散图如图9~10所示。
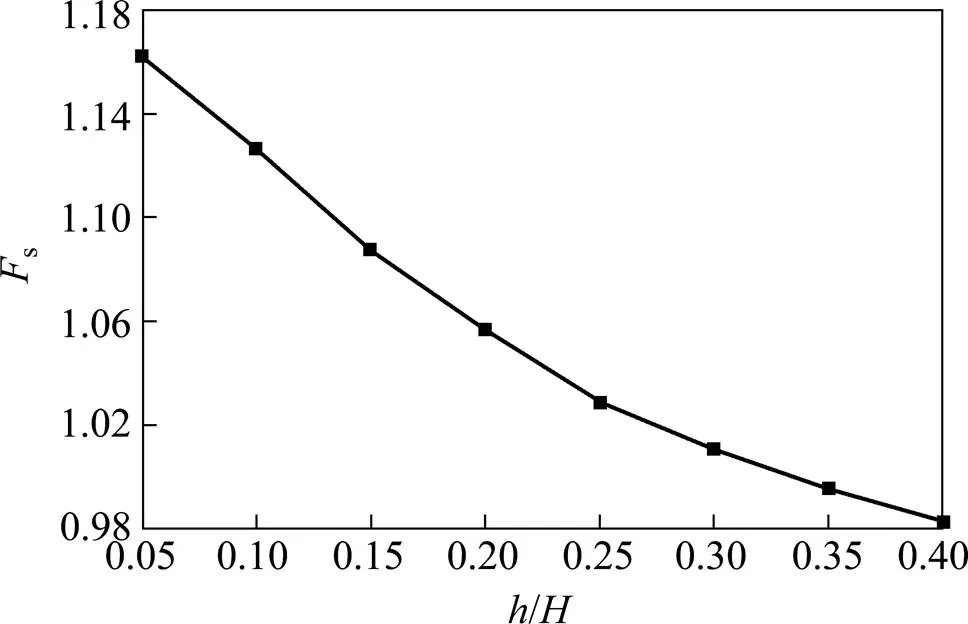
图9 软弱夹层厚度对边坡安全系数Fs的影响
由图9可以看出,边坡的安全系数随着软弱夹层厚度的增大而减小。从图10可以看出,随着软弱夹层厚度逐渐增大,破坏的范围逐渐增大,滑裂面逐渐变深向边坡软弱夹层下界面扩展,且滑裂面始终贯穿软弱夹层上界面与下界面相切,其剪出口位置往坡趾外移动,坡面处剪切带逐渐消失。因此,软弱夹层厚度是有必要考虑的,仅假设为无厚度的直线在一定程度上会夸大边坡的稳定性。
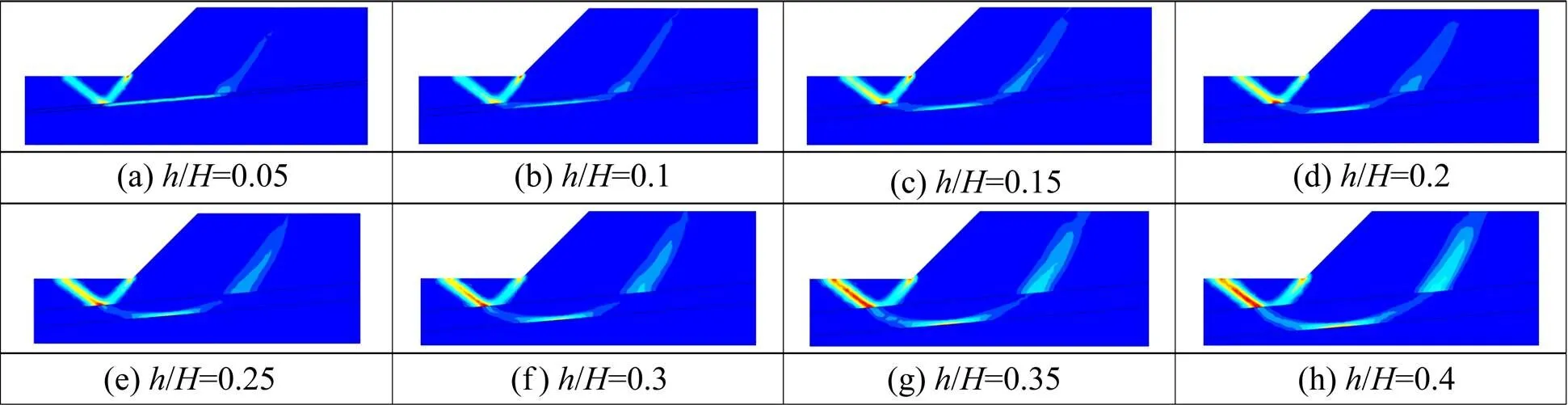
图10 不同软弱夹层厚度下的边坡能量耗散图
3.2 软弱夹层倾角对边坡稳定性的影响
在3.1节基础上,令/=0.1,其中取值为0°~10°。经计算求解可得不同软弱夹层倾角情况下的边坡安全系数及其相应塑性区能量耗散图如图11~12所示。
由图11可看出,随着软弱夹层倾角的增加,安全系数显著减小。由图12可看出,随着软弱夹层倾角的增加,滑裂面的剪出口向坡趾移动,滑动面逐渐变浅向临空面收缩,坡面处剪切带逐渐 消失。
3.3 夹层与土体相对强度对边坡稳定的影响
令/=0.1,=5°,/=0.5,土体强度参数1=20 kPa,1=20°,软弱夹层与土体的相对强度2/1= 0.15~0.7,2/1=0.15~0.7,2/1和2/1取相同的值,其中土体自重均为=20 kN/m3。经优化计算,整理得到不同软弱夹层与土体的相对强度下边坡的安全系数与能量耗散图如图13~14所示。
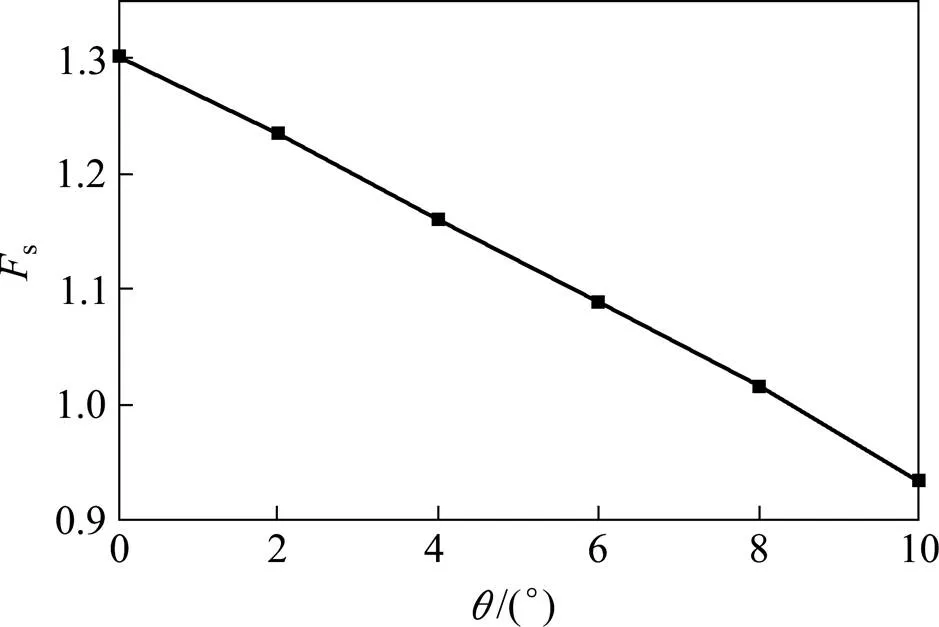
图11 软弱夹层倾角θ对边坡安全系数Fs的影响
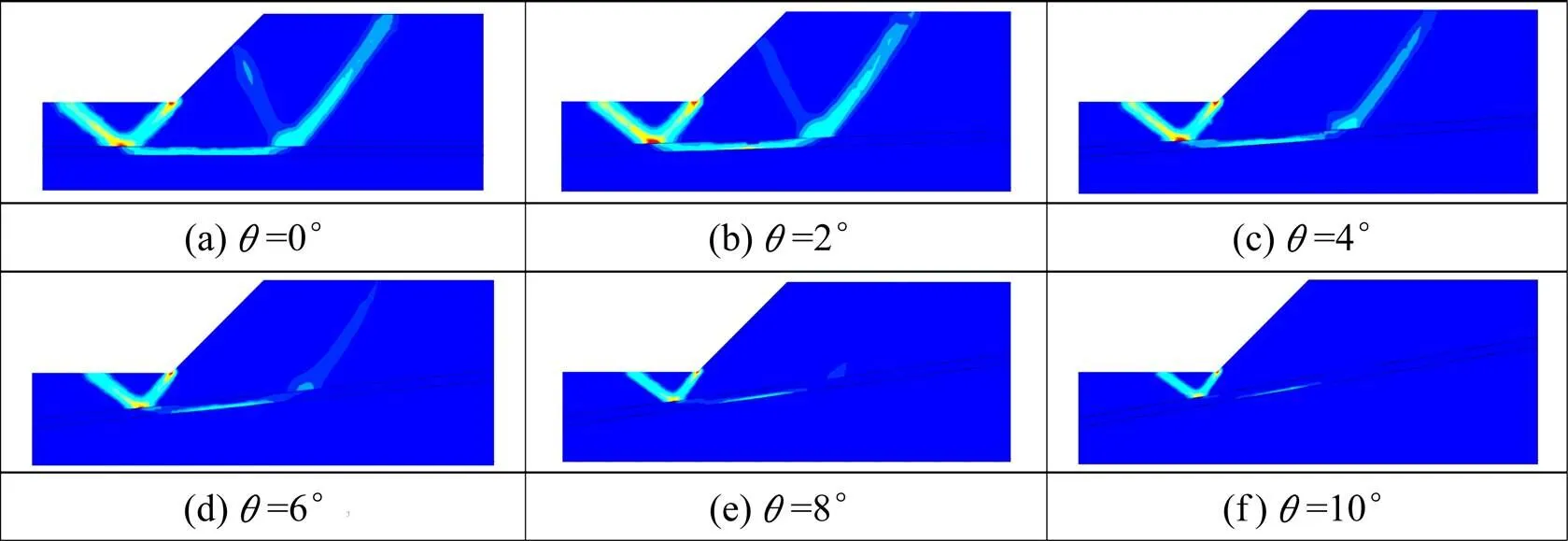
图12 不同软弱夹层倾角θ值下的边坡能量耗散图
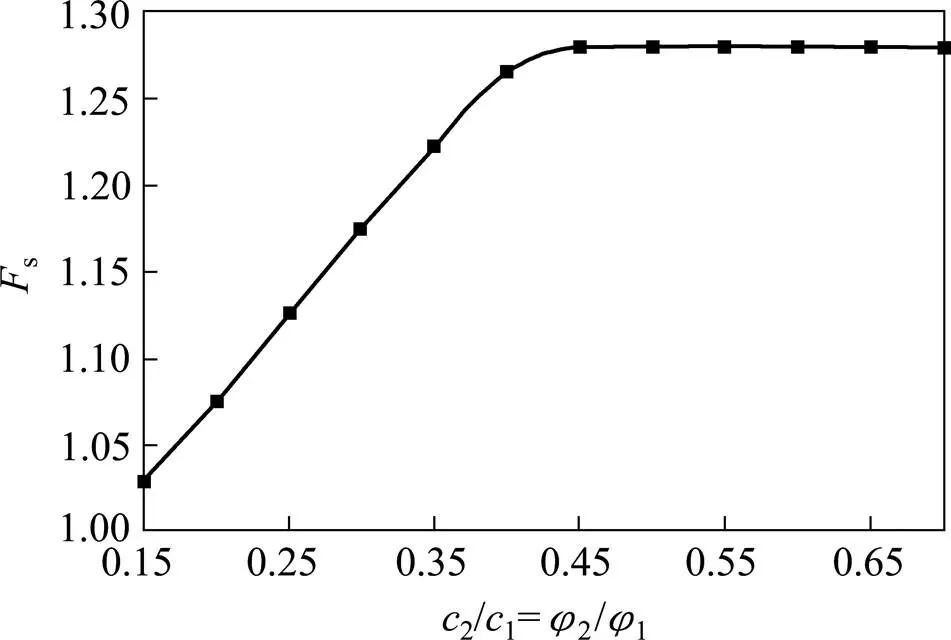
图13 软弱夹层与土体的相对强度对边坡安全系数Fs的影响
由图13可以看出,边坡的安全系数随着软弱夹层与土体的相对强度增加而增加,当软弱夹层与土体的相对强度超过0.45时,结果保持不变s= 1.28。同样的,由其对应塑性区能量耗散图(图14(a)~14(g)),可以看出随着软弱夹层与土体的相对强度的逐渐增大,滑裂面区域逐渐减小,坡面处剪切带逐渐出现再消失,滑裂面与软弱夹层相切,剪出口逐渐向坡趾移动;当软弱夹层与土体的相对强度超过0.45后,剪出口位于坡趾,滑裂面仅发生在过坡趾的上层土体且不再发生变化,如图14(h)~ 14(l)。说明此时软弱夹层不再影响边坡的稳定性。
3.4 软弱夹层深度对边坡稳定性的影响
令/=0.1,=5°,其中/=0.2~0.5。岩体强度参数1=20 kPa,1=20°,考虑2种软弱夹层与土体的相对强度2/1=2/1=0.25和2/1=2/1=0.5,其中土体自重均为=20 kN/m3。经计算求解可得软弱夹层深度下边坡安全系数及其相应的能量耗散图如图15~16所示。
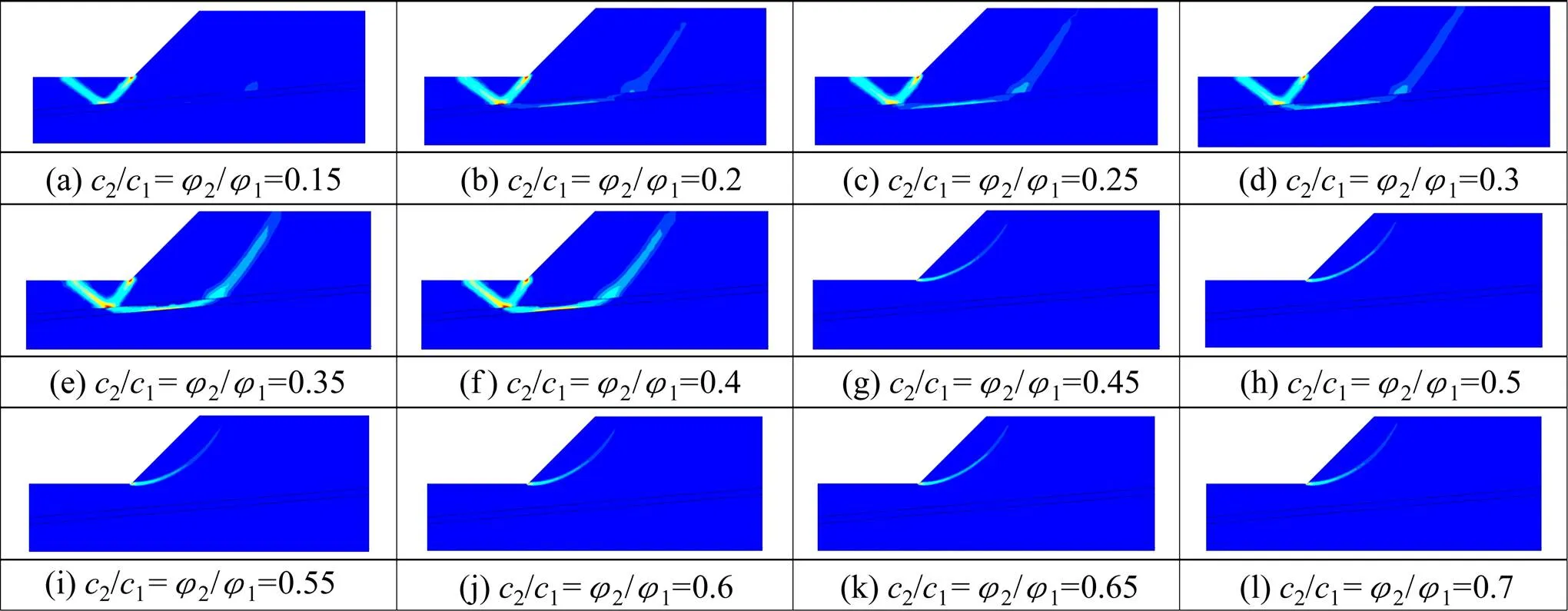
图14 不同软弱夹层与土体的相对强度下边坡能量耗散图
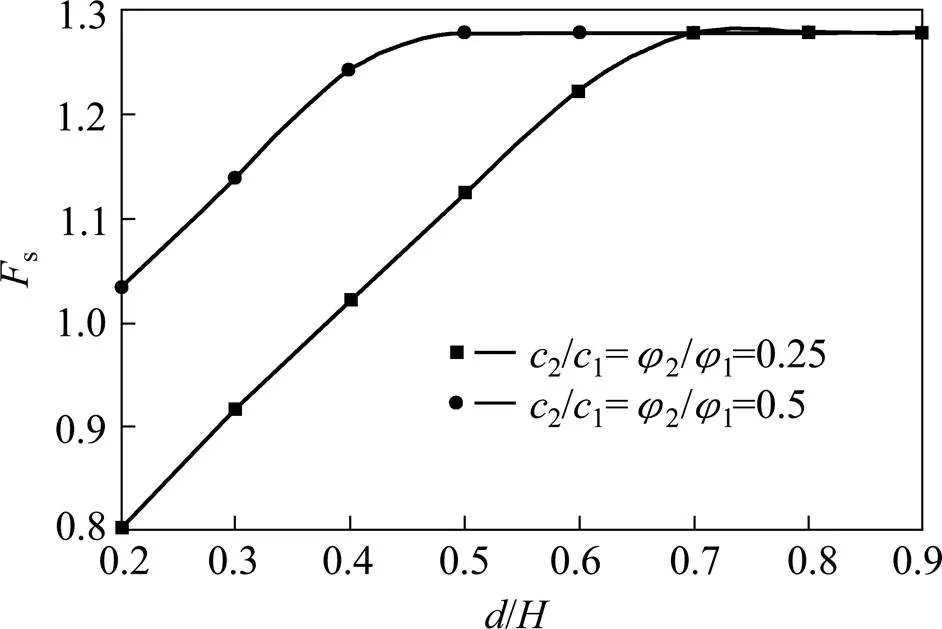
图15 软弱夹层深度对边坡安全系数Fs的影响
由图15可以看出,对于2种软弱夹层与土体的相对强度情况,边坡的安全系数均随着软弱夹层深度增大先增加后保持不变s=1.28,在达到定值之前,软弱夹层与土体的相对强度越高安全系数越大且在深度较小时就达到定值。同样的,由图16可以得知,随着软弱夹层深度增加,滑裂区域逐渐加深增大,滑裂面与软弱夹层相切,剪出口逐渐向坡趾反方向移动;当软弱夹层深度/超过0.7 (2/1=2/1=0.25时)或0.5(2/1=2/1=0.5时)后,剪出口位于坡趾,滑裂面仅发生在过坡趾的上层土体且 不再发生变化如图,14(f)~14(h)和图14(d)~14(h)。说明此时软弱夹层不再影响边坡的稳定性。
特别地,对于含软弱夹层边坡稳定性分析,由本文方法获得的破坏模式具有不同形式,包括文献[13]中的改进转动−平动组合破坏机构(如图16(b))和直线滑动破坏机构(如图16(d)),以及文献[9−10]中的转动−平动组合破坏(如图16(j)),另外也包含有其他一些破坏模式(如图16(a),16(c)和16(f))。这是因为含软弱夹层边坡破坏具有复杂性,会造成破坏模型的假定不完全符合实际情况,这证明了本文方式不需要提前假定破坏模式所带来的优势,使得模拟的结果更加符合工程实际。
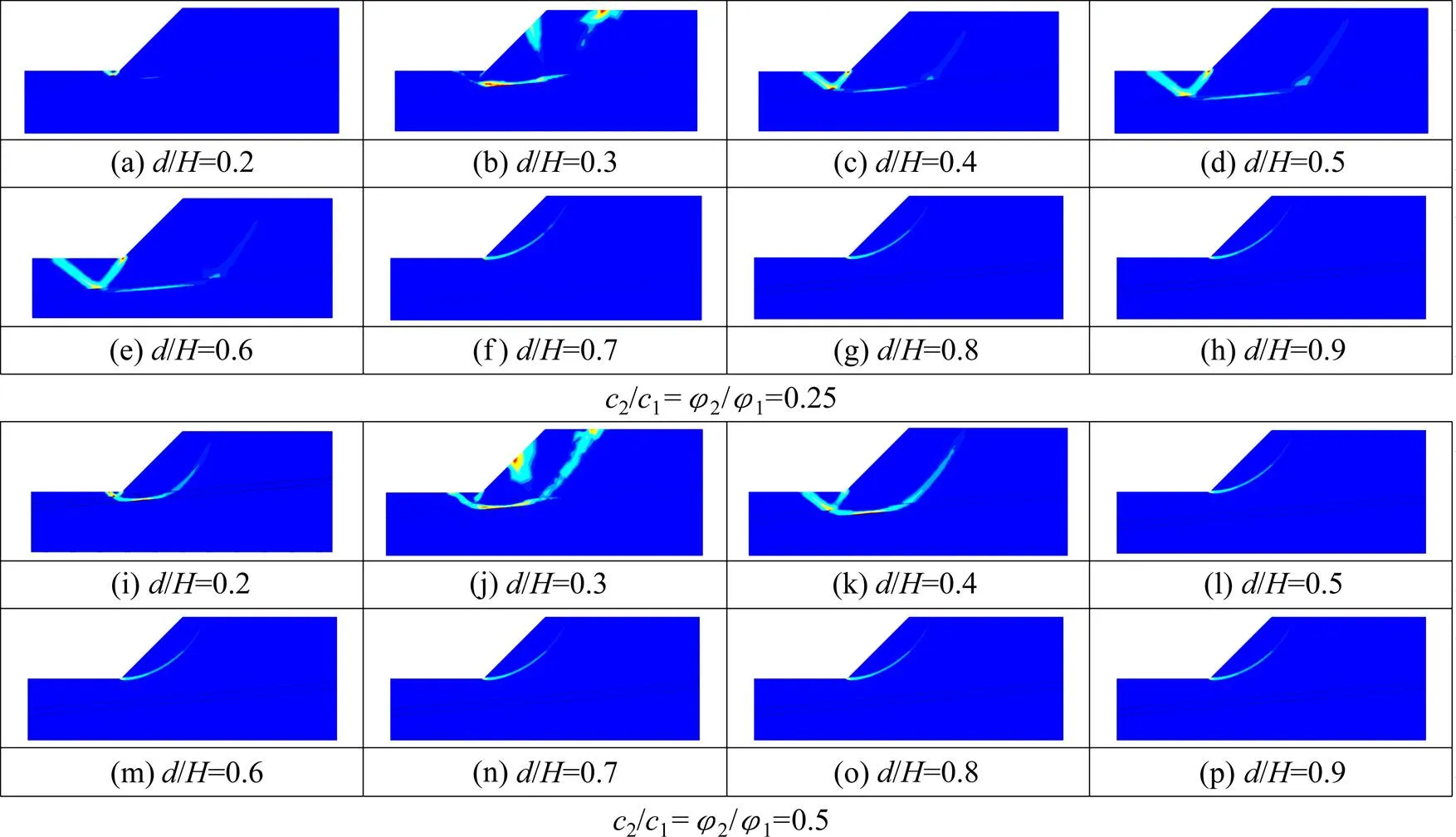
图16 不同软弱夹层深度下的边坡能量耗散图
4 结论
1) 将强度折减技术引入有限元极限上限法中,获得了含软弱夹层边坡安全系数的上限解。通过经典算例的验证和对比,本文获得计算结果和已有研究成果非常接近甚至更优,表明该方法所得的结果和规律具较高的可靠性。另外通过破坏模式形式的对比可知,本文方法获得的破坏模式更加符合工程实际。
2) 随着软弱夹层厚度逐渐增大,边坡的安全系数减小,破坏的范围逐渐增大,滑裂面逐渐变深向边坡软弱夹层下界面扩展,且滑裂面始终贯穿软弱夹层上界面与下界面相切,其剪出口位置往坡趾外移动,坡面处剪切带逐渐消失。
3) 软弱夹层倾角对边坡的稳定性影响显著。随着软弱夹层倾角的增加,安全系数显著减小,滑裂面的剪出口向坡趾移动,滑动面逐渐变浅向临空面收缩,坡面处剪切带逐渐消失。
4) 当软弱夹层强度相对较小时,边坡的安全系数随着软弱夹层与土体的相对强度增加而增加,滑裂面区域逐渐减小,坡面处剪切带逐渐出现再消失,滑裂面与软弱夹层相切,剪出口逐渐向坡趾移动;当软弱夹层与土体的相对强度超过0.45时,安全系数不再变化,此时边坡破坏仅发生在过坡趾的上层土体,表现为简单均质边坡破坏且不再发生变化。说明此时软弱夹层不再影响边坡的稳定性。
5) 软弱夹层深度对边坡的稳定性影响与软弱夹层与土体的相对强度相关。边坡的安全系数随着软弱夹层深度增大先增加后保持不变,且软弱夹层与土体的相对强度越高,安全系数达到定值时的软弱夹层深度越小。同时,随着软弱夹层深度增加,滑裂区域逐渐加深增大,剪出口逐渐向坡趾反方向移动;当软弱夹层深度/超过0.7(2/1=2/1= 0.25时)或0.5(2/1=2/1=0.5时)后,剪出口位于坡趾,滑裂面仅发生在过坡趾的上层土体且不再发生变化。说明此时软弱夹层不再影响边坡的稳定性。
[1] 闫汝华, 樊卫花. 马家岩水库坝基软弱夹层剪切特征及强度[J]. 岩石力学与工程学报, 2004, 23(11): 3761−3764. YAN Ruhua, FAN Weihua. Shear properties and strength of weak intercalated layers in dam foundation of Majiayan reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(22): 3761−3764.
[2] 郭洪江, 张霖, 赵文恺. 成昆线林场滑坡病害治理工程[J]. 西南交通大学学报, 1996, 31(6): 685−690. GUO Hongjiang, ZHANG Lin, ZHAO Wenkai. The reinforcement and renovation of Linchang landslide along Chengdu Kunming railway[J]. Journal of Southwest Jiaotong University, 1996, 31(6): 685−690.
[3] CHAI J, ZHANG Y, BO L I, et al. The influences of weak interlayer on rocky slope stability under the condition of excavation[J]. Engineering Construction, 2017, 49(2): 1− 6.
[4] 张社荣, 谭尧升, 王超, 等. 多层软弱夹层边坡岩体破坏机制与稳定性研究[J]. 岩土力学, 2014, 35(6): 1695−1702. ZHANG Sherong, TAN Yaosheng, WANG Chao, et al. Research on deformation failure mechanism and stability of slope rock mass containing multi-weak interlayers[J]. Rock and Soil Mechanics, 2014, 35(6): 1695−1702.
[5] 宋子岭, 杨添, 赵立春. 含多层软弱夹层的顺向岩质边坡稳定性评价方法对比分析[J]. 中国地质灾害与防治学报, 2016, 27(2): 20−25. SONG Ziling, YANG Tian, ZHAO Lichun, et al. Applicatyion of combination algorithm in stability analysis of rock slope with contains multilayer weak bedrock layers[J]. Chinese Journal of Geological Hazard & Control, 2016: 27(2): 20−25.
[6] 许宝田, 钱七虎, 阎长虹, 等. 多层软弱夹层边坡岩体稳定性及加固分析[J]. 岩石力学与工程学报, 2009, 28(增2): 3959−3964. XU Baotian, QIAN Qihu, YAN Changhong, et al. Stability and strengthening analyses of slope rock mass containing multi-weak interlayers[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Suppl 2): 3959−3964.
[7] CHEN W F. Limit analysis and soil plasticity[M]. Amsterdam: Elsevier ASCE, 1975.
[8] 刘小丽, 周德培. 有软弱夹层岩体边坡的稳定性评价[J]. 西南交通大学学报, 2002, 37(4): 382−386. LIU Xiaoli, ZHOU Depei. Stability evaluation of rock mass slope with weak intercalated layers[J]. Journal of Southwest Jiaotong University, 2002, 37(4): 382−386.
[9] 黄茂松, 王浩然, 刘怡林. 基于转动-平动组合破坏机构的含软弱夹层土坡降雨入渗稳定上限分析[J]. 岩土工程学报, 2012, 34(9): 1561−1567.HUANG Maosong, WANG Haoran, LIU Yilin. Rotation- translation combined mechanism for stability analysis of slopes with weak interlayer under rainfall condition[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(9): 1561−1567.
[10] HUANG Maosong, WANG Haoran, SHENG Daichao, et al. Rotational–translational mechanism for the upper bound stability analysis of slopes with weak interlayer[J]. Computers and Geotechnics, 2013(53): 133−141.
[11] ZHAO Lianheng, LI Liang, YANG Feng, et al. Upper bound analysis of slope stability with nonlinear failure criterionbased on strength reduction technique[J]. Journal of Central South University of Technology, 2010, 17(4): 836−844.
[12] 赵志刚, 赵炼恒, 李亮, 等. 水位升降对顺层岩坡稳定性影响的上限分析方法[J]. 铁道科学与工程学报, 2012, 9(3): 51−57. ZHAO Zhigang, ZHAO Lianheng, LI Liang, et al. Upper bound stability analysis for parallel bedding rock slope subjected to water level fluctuations[J]. Journal of Railway Science and Engineering, 2012, 9(3): 51−57.
[13] 汤祖平, 李亮, 赵炼恒, 等. 含软弱夹层边坡稳定性的极限分析上限解析[J]. 铁道科学与工程学报, 2014, 11(2): 60−64. TANG Zuping, LI Liang, ZHAO Lianheng, et al. Stability analysis of slopes with weak interlayer based on upper bound limit analysis[J]. Journal of Railway Science & Engineering, 2014, 11(2): 60−64.
[14] 王均星, 王汉辉, 张优秀, 等. 非均质土坡的有限元塑性极限分析[J]. 岩土力学, 2004, 25(3): 415−421. WANG Junxing, WANG Hanhui, ZHANG Youxiu, et al. Stability analysis of soil slope by finite element method with plastic limit upper bound[J]. Chinese Journal of Rock Mechanics & Engineering, 2004, 25(3): 415−421.
[15] 赵明华, 张锐. 有限元上限分析网格自适应方法及其工程应用[J]. 岩土工程学报, 2016, 38(3): 537−545.ZHAO Minghua, ZHANG Rui. Adaptive mesh refinement of upper bound finite element method and its applications in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(3): 537− 545.
[16] Lyamin A V, Sloan S W. Upper bound limit analysis using linear finite elements and nonlinear programming[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(2): 181−216.
[17] Thompson J F, Soni B K, Weatherill N P. Hand book of grid generation[M]. Boca Raton London New York Washington D C: CCR Press, 1998.
[18] Sloan S W. Geotechnical stability analysis[J]. Géotechnique, 2013, 63(7): 531−572.
[19] 赵明华, 张锐, 雷勇. 基于可行弧内点算法的上限有限单元法优化求解[J]. 岩土工程学报, 2014, 36(4): 604−611. ZHAO Minghua, ZHANG Rui, LEI Yong. Optimization of upper bound finite element method based on feasible arc interior point algorithm[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 604− 611.
[20] Abbo A J, Sloan S W. A smooth hyperbolic approximation to the Mohr-Coulomb yield criterion[J]. Computers and Structures, 1989, 36: 19−38.
Stability analysis for soil slopes with weak interlayers using the finite element upper bound limit analysis
PI Xiaoqing, LI Liang, TANG Gaopeng, ZHANG Rui, ZHAO Lianheng
(School of Civil Engineering, Central South University, Changsha 410075, China)
The existence of weak interlayers usually makes the slope more prone to instability. Based on this, by introducing the finite element upper bound limit analysis method considering the strength reduction technique, the nonlinear programming model for the stability analysis of slopes with a weak interlayer was constructed. And a feasible arc interior point algorithm, combined with adaptive mesh method, was adopted for optimization. The upper-bound solutions of safety factors and failure modes of slopes with different weak interlayer thicknesses, angles and depths and strength ratios of the weak interlayer and soil were obtained. The results show that the thickness, angle, depth and relative strength of the weak interlayer have significant influence on the safety factor of slope and the critical sliding surface, but when the depth and relative strength of the weak interlayer are increased to a certain value, the stability of the slope is no longer affected by it. The results in this paper are in good agreement with those in the literature.
slope stability analysis; weak interlayer; upper bound limit analysis; safety factor
10.19713/j.cnki.43−1423/u.2019.02.010
TU435
A
1672 − 7029(2019)02 − 0351 − 08
2018−03−12
国家自然科学基金资助项目(51478477);中南大学中央高校基本科研业务费专项资金资助项目(2017zzts746)
唐高朋(1989−),男,湖南邵阳人,博士研究生,从事道路与铁道工程方面的研究与应用工作;E−mail:381588836@qq.com
(编辑 涂鹏)
