基于随机森林和最小角回归的结构地震需求重要性度量分析
2019-02-22王秀振钱永久
王秀振, 钱永久, 宋 帅
(1. 西南交通大学 土木工程学院,成都 610031; 2. 太原理工大学 建筑与土木工程学院,太原 030024)
在工程抗震计算中,结构地震需求分析是地震易损性分析的重要基础,近些年结构地震需求分析的研究成果较多。陈亮等[1]进行了非线性动力分析,发现在高频区段的大跨径桥梁中,反应谱对其结构地震需求的影响很大。刘骁骁等[2]计算了框架结构基于概率地震需求分析的多维的地震易损性,描述了对多个输入随机参数敏感的结构的破坏现象。周世军等[3]以概率地震需求模型,基于已有数据,分析了预应力简支箱梁桥的地震需求,研究发现两次非线性回归方法的概率需求模型比线性回归分析方法的概率需求模型更可靠。
局部敏感性分析是不确定性分析领域传统的研究方法,通过研究输入随机变量在指定的名义值变化时,输出反应量的变化来研究输入随机变量对输出反应量的影响程度[4]。除此之外,还有一种不确定分析领域的研究方法:重要性度量分析,这是一种全局敏感性分析方法,可以研究输入随机变量在所有可能的取值处变化时,输出反应量的变化情况[5]。重要性分析常用方法有点估计法[6]、态相关参数法[7]和Monte-Carlo数值模拟法[8]等。
宋帅等[9]为了分析桥梁中的输入随机变量对地震需求的影响,提出用全局敏感性分析方法对输入随机变量进行了重要性排序。尹犟等[10]对钢筋混凝土框架进行了局部敏感性分析,采用3种方法研究了地震动强度和结构中的输入随机变量对4种结构地震需求的影响程度。发现地震动强度对结构地震需求的影响最为显著,结构质量、混凝土的抗压强度以及结构阻尼的影响也较大,其他输入随机变量的影响比较小。董现等[11]针对蒙特卡罗方法出现的计算速度慢和未考虑输入随机变量之间的相关性问题,采用混沌粒子群算法,考虑了输入随机变量的相关性,通过等效变换的随机序列进行了随机性分析,提出了灵敏性测度方法,发现所提出的方法是很好地反映灵敏性的方法。
本文提出将随机森林算法和最小角回归算法应用到输入随机变量对输出反应量的重要性度量分析中,以带黏滞阻尼器的钢筋混凝土框架结构为例,对影响框架结构地震需求的结构中的输入随机变量进行了重要性度量分析,并同时用Monte-Carlo数值模拟法进行对比,验证两种方法的有效性以及高效性。
1 重要性度量方法
1.1 基于随机森林的重要性度量方法
1.1.1 随机森林基本原理
2001年,Bremain结合划分随机子空间策略的方法和Bagging学习理论,提出随机森林算法(Random Forest, RF),以分类回归树作为它的元分类器。
随机森林有回归和分类两种技术,随机森林回归算法是在随机子空间策略方法和Bagging学习理论基础上,提出来的一种集成的算法。
每棵分类回归树在生成时,随机森林回归算法都是独立的抽取特征和样本,随机森林回归的就是生成多棵分类回归树的过程,因此天生的可并行性是随机森林回归的一大特点,所以运行时间可以大大减少。
如图1所示,每一棵CART树的构建,都要用Bootstrap重抽样方法从大小为n的训练子样本集中抽样,使构建CART树的具体数据有差别,然后将多棵CART树的预测结果进行组合,利用投票的方法得出最终结果。

图1 随机森林回归示意图Fig.1 Random forest regression sketch map
1.1.2 结构地震需求获得方法
(1) 首先抽取N个低偏差的sobol序列样本,根据各个输入随机变量的概率密度函数转化为相应的样本值,N个输入随机变量的样本值排为一列,假设有n个输入随机变量,则可得到所有样本值的N×n维的样本矩阵
(1)
(2) 将矩阵A中的各个样本值输入到OpenSEES软件的模型中,计算输出反应量(结构地震需求),产生N个结构地震需求Y的样本值
(2)
1.1.3 重要性度量方法
总体训练样本集采用重抽样方法抽样后,每个样本不被抽中的概率是(1-1/N)N,其中N代表总体训练样本集的样本数。当N较大时,(1-1/N)N收敛于1/e≈0.368,这表明总体训练样本集中大概有36.8%的“袋外数据”(Out of Bag, OOB)会不在训练子样本集中,所以可用它们作为测试数据集来评价随机森林预测性能,这种方法方法称为OOB估计(Out of Bag Estimation ),相应的指标成为%IncMSE。若随机森林中决策树的数量足够多,OOB估计具有无偏性的特点[12-13]。
随机改变随机森林模型中某个输入随机变量时(噪声扰动),可以将扰动对随机森林模型的影响程度作为该输入随机变量相对重要性的度量,在随机森林回归分析时,可以采用“袋外数据”估计的均方误差的平均递减值来评价输入随机变量对回归模型的重要性,均方误差的定义是
(3)

1.2 基于最小角回归的重要性度量方法
1.2.1 最小角回归基本原理
2004年,Efron等[14]提出了最小角回归(Least Angle Regression, LARS)算法,最小角回归算法的步骤如图2所示,具体如下[15]:
步骤1判断输入自变量x与输出反应量y的相关度,然后用有最大相关度的输入自变量xi对y逼近;
步骤2找到另一个与y具有相同相关度的输入自变量xj,即rxiy=rxjy, 然后从xi与xj的角平分线方向xu逼近y;
步骤3同理,若出现第3个输入自变量xk与输出反应量y的相关度与xi相同, 则将xk也纳入到逼近列队,选择3个向量共同的角平分线方向xv施行新一轮的逼近,此时角平分线方向表示多维空间中多个向量的平分线方向;
步骤4逐步逼近直到所有输入自变量都参与到逼近中,或者残差小于某个设定的阈值时,结束算法。

图2 LARS计算步骤Fig.2 LARS calculation procedure

1.2.2 重要性度量方法
假设输出反应量(结构地震需求)的N个样本值为yk(k=1,2,…,N), 结构地震需求Y的总方差为
(4)


(5)

则基于最小角回归模型的重要性度量指标Si
(6)
对于输入随机变量为n维时,用n个输入随机变量分别代入随机森林回归模型中,得到预测值,然后得到所有输入随机变量的重要性度量指标Si(i=1,2,…,n)。
1.3 Monte-Carlo数值模拟法
1.3.1 基于方差的重要性度量指标

(7)
式中:Xi为输入随机变量组[Xi1,Xi2,…,Xir](1≤i1≤…≤ir≤n)或输入随机变量Xi,E(Var(Y|Xi))是Xi作用下,Y的条件方差的均值。
1.3.2 求解方法
准蒙特卡洛法是抽样方法中需要样本量较少的一种方法,为了在样本量较少的情况下仍然得到较好的结果,本文采用低偏差的Sobol序列(当样本量达到500左右时,方差和数学期望的偏差在千分之一以内),根据各个输入随机变量的概率密度函数转化为相应的样本,样本量为几百即可得到合理的结果,具体如下:

结构地震需求Y的无偏无条件方差Var(Y)如式(4)所示, 无偏条件方差Var(Y|Xi)为
(8)

1.4 计算流程

图3 计算流程Fig.3 Calculation process
2 工程实例
某7层3跨的钢筋混凝土框架结构,黏滞阻尼器的阻尼指数为1,底层层高4 200 mm,标准层层高3 600 mm,如图 4所示。柱距均为6 000 mm,楼板的厚度为120 mm,混凝土强度等级为C40,钢筋强度等级为HRB335,输入随机变量的信息,如表1所示。

图4 结构简图Fig.4 Structure diagram
输入随机变量变异系数均值分布类型黏滞阻尼器的阻尼系数c/(kN·s·mm-1)0.13正态黏滞阻尼器的刚度k/(kN·mm-1)0.1100正态阻尼比DA0.2[16]0.055正态结构质量Ms/(kN·m-2)0.1[17]6正态钢筋屈服强度fy/MPa0.078[18]384对数正态钢筋弹性模量Es/MPa0.033[19]228 559正态混凝土强度fc/MPa0.1434.82正态混凝土弹性模量Ec/MPa0.08[20]33904正态注:表中结构质量取为重力荷载代表值
本文地面运动加速度采用El Centro地震波,用OpenSees有限元软件进行非线性动力时程分析,运用Maxwell单元模拟黏滞阻尼器,柱和梁都采用宏观的非线性纤维梁柱单元,钢筋采用Steel02单元材料模型,混凝土采用Concrete02单元材料模型,选择基底剪力、顶点位移和最大层间位移角这3种地震需求进行重要性度量分析。
3 重要性度量分析结果
3.1 基于随机森林的重要性度量指标
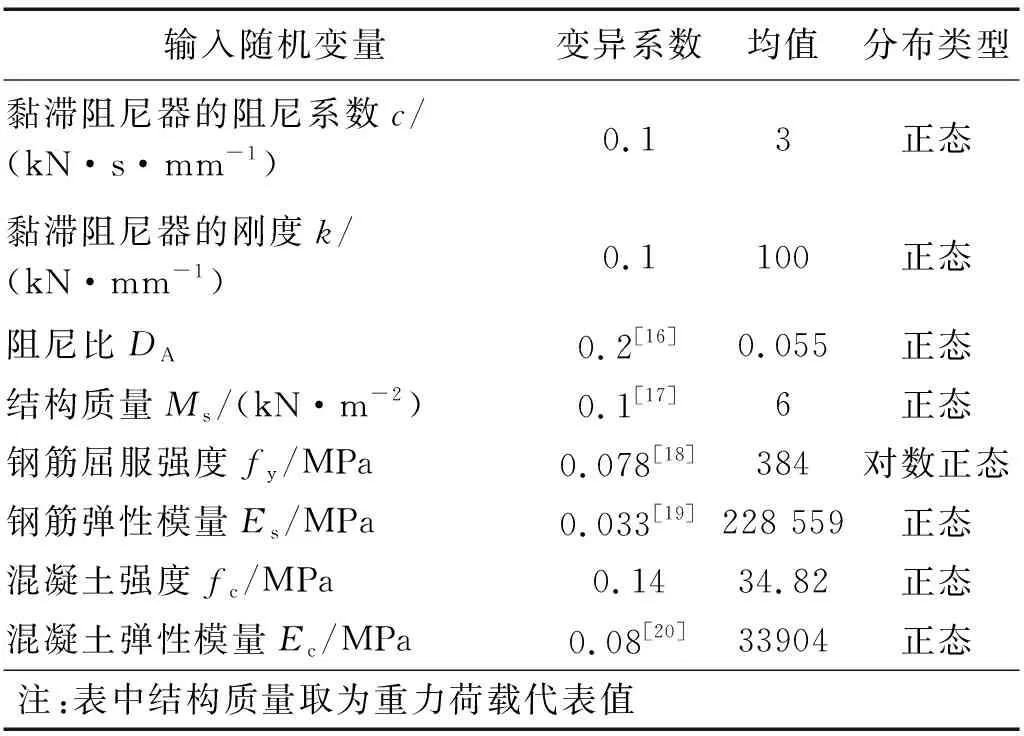
图5给出了基于随机森林的重要性度量指标,从图5可知,同一输入随机变量对3种不同的地震需求的影响水平不尽相同,但黏滞阻尼器的刚度和混凝土的弹性模量对3种地震需求的影响都较小。
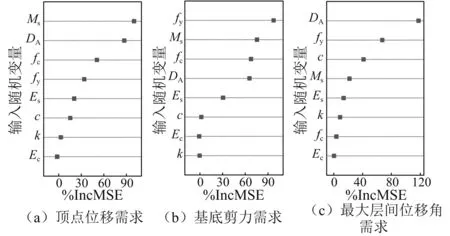
图5 随机森林重要性度量指标Fig.5 Random forest importance measure index
3.2 基于最小角回归的重要性度量指标
图6给出了基于最小角回归的各个输入随机变量对应的最大层间位移角需求的预测值趋势线,从图中可以看出,阻尼比、钢筋的屈服强度和黏滞阻尼器的阻尼系数所对应直线的斜率较大,而混凝土的抗压强度和弹性模量以及黏滞阻尼器的刚度所对应直线的斜率较小。由于篇幅所限,其他两种地震需求的预测值趋势线不再一一列出。

图6 LARS最大层间位移角需求预测值Fig.6 The predicted value of LARS’ most story drift angle demand
图7给出了基于最小角回归和Monte-Carlo数值模拟法的重要性度量指标结果,从图7可知,Ms和DA对结构地震需求的影响最大,而Ec和k的影响都很小。
图7 不同方法重要性度量指标Fig.7 Importance measure index under different methods
4 结果对比
本文采用3种方法进行重要性度量分析,都是是全局敏感性分析方法。为便于对用3种方法的重要性度量结果进行对比,将3种方法得到的输入随机变量的重要性度量分析排序结果列于表2中。

表2 输入随机变量的重要性排序
由表3可知,采用3种方法得到的输入随机变量的重要性度量分析排序,除极个别稍有差别外,基本完全一致,3种分析方法的结果均表明:钢筋的屈服强度和阻尼比对3种结构地震需求的影响都很显著,黏滞阻尼器的刚度和混凝土的弹性模量的影响都较小。

5 结 论
本文通过随机森林和最小角回归方法,对一带黏滞阻尼器的钢筋混凝土框架结构进行了非线性动力时程分析,得到了3种结构地震需求,对8个输入随机变量进行了重要性度量分析,并通过Monte-Carlo数值模拟法进行对比,得到如下结论:
(1) 对于同一种结构地震需求,采用3种不同分析方法时,输入随机变量的重要性排序基本相同。
(2) 基于随机森林和最小角回归的重要性度量分析方法与Monte-Carlo数值模拟法相比,在总样本量少很多的情况下,得到的重要性排序结果与Monte-Carlo数值模拟法基本相同。
(3) 同一输入随机变量对结构的3种不同结构地震需求的重要性排序差别较大,即同一输入随机变量对不同地震需求的影响水平基本不同。
(4) 对于本文的3种不同结构地震需求,采用上述3种不同的重要性度量分析方法时,阻尼比、结构质量和钢筋的屈服强度的重要性排序均靠前;而黏滞阻尼器的刚度和混凝土的弹性模量的重要性排序均靠后。
通过不同分析方法的对比可见,本文提出的基于随机森林和最小角回归的重要性度量分析方法是高效准确的方法,在复杂结构的重要性度量分析中可以使样本量大大减少,这对结构抗震具有重要的参考意义。
