抗混叠失真IIR数字滤波器的设计与仿真①

刘文斐

(齐鲁师范学院物理与电子工程学院，山东 济南 250200)

0 引 言

混叠失真[1]是指在信号采样过程中发生的频谱混叠现象，在对连续时间信号进行等间隔采样时，如果信号的最高频率成分大于采样频率的一半，即不满足奈奎斯特采样定理，那么采样后高于和低于采样频率的信号将混杂在一起，信号的频谱发生频谱分量的交叠现象，这就是频谱混叠失真。发生频谱混叠失真的信号将无法重建，也就是信号将无法从采样信号中进行恢复还原。

1 IIR数字滤波器的设计中发生混叠失真的原因

IIR(infinite impulse response)滤波器是数字滤波器中的一种。数字滤波器按照系统的冲激响应的特点可以分成无限长单位冲激响应IIR滤波器和有限长单位冲激响应FIR(finite impulse response)滤波器。IIR滤波器[2]具有结构简单、效率高、与模拟滤波器有对应关系、易于解析控制及计算机辅助设计等优点，与FIR滤波器相比，相同阶次滤波效果更好。

IIR数字滤波器一般采用间接设计的方法。间接法设计是利用模拟滤波器来设计数字滤波器，因为模拟滤波器的设计方法已经比较成熟，有完整的设计公式以及数据表格可以直接使用，使得数字滤波器的设计更为方便、高效和快捷。在利用模拟滤波器设计数字滤波器的间接法设计过程中，需要设计出归一化的原型模拟低通滤波器，然后将原型模拟滤波器的系统函数H(s)数字化变换成所需要的数字滤波器的系统函数H(z)，即把复数平面s平面映射到z平面上。模拟滤波器数字化方法较常采用的是冲激响应不变法和双线性变换法。

冲激响应不变法[3]是从滤波器的单位抽样响应出发，使数字滤波器的单位抽样响应h(n)逼近模拟滤波器的单位抽样响应h(t)，频率间的变化是线性变换关系，克服了双线性变换法中非线性频率变换带来的临界频率点的频率畸变，所以是最简单、最直接的一种把s平面映射到z平面的映射方法。但是这种方法要求模拟滤波器是严格带限于抽样频率的一半，如果不满足该要求，数字滤波器的频率响应将产生混叠失真。

2 由冲激响应不变法产生混叠失真的解决方案

由于高通滤波器和带阻滤波器它们的幅度响应在频率大于抽样频率的一半时仍不衰减，即不是严格带限的，所以如果使用冲激响应不变法在设计的时候会发生频谱的混叠失真。基于该前提条件，是否冲激响应不变法不能够设计高通和带阻滤波器呢？如果需要使用冲激响应不变法进行设计怎样能够消除在设计过程中产生的频谱混叠失真呢？经研究发现，如果使用“模拟-模拟频带变换”的方法设计IIR数字高通或者是带阻滤波器，冲激响应不变法确实会产生混叠失真现象，但是如果使用“数字-数字频带变换”的方法则不存在该问题。

所谓“模拟-模拟频带变换”[3]的方法是先由给定的技术指标设计归一化样本的模拟低通滤波器，然后利用模拟频带变换成其他模拟各种(低通、高通、带通、带阻)滤波器，最后将模拟滤波器数字化成相应的数字滤波器，频带变换在模拟信号域中进行，对模拟滤波器的运算设计因为有公式和表格直接使用，所以也是相对来说较常使用的一种方法。与之相区别的“数字-数字频带变换”[3]的方法是由给定的技术指标设计归一化样本的模拟低通滤波器，然后直接数字化成为数字低通滤波器，再将数字低通利用数字频带变换成其他各种通带的数字滤波器，频带变换在数字信号域中进行，需要找到不同数字频带间的函数关系。使用“数字-数字频带变换”的方法能够克服冲激响应不变法在模拟滤波器的数字化映射过程中的频谱混叠，这是因为在这种方法中的数字化过程是将模拟低通滤波器的系统函数映射为数字低通滤波器的系统函数，模拟低通滤波器是严格带限于抽样频率的一半的、是抗混叠的，所以不存在频率混叠失真现象。

3 抗混叠滤波器设计实例

设计要求：设计一个巴特沃斯数字带阻滤波器，其技术指标为：在通带频率小于6kHz和大于14kHz的范围内，衰减不大于2dB，阻带截止频率分别为8kHz和12kHz，阻带内衰减不小于20dB，抽样频率为400kHz。

对于巴特沃斯滤波器来说，通带的截止频率是指幅频大小下降为最大值的0.707倍，即幅度衰减3dB对应的频率值，给定的技术指标中的通带频率不一定为通带截止频率。

根据计算滤波器阶数为：

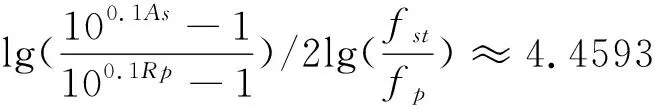
通带截止频率为

其中RP=2dB，AS=20dB，fp=6kHz，fst=8kHz

如果利用“模拟——模拟频带变换”的方法通过冲激响应不变法完成模拟滤波器的数字化过程设计，设计步骤为：

(1)将待求数字滤波器(DF)的设计指标转化为模拟低通滤波器(AF)的指标；

(4)利用冲激响应不变法将H(s)转化为待求带阻DF的H(z)。

利用MATLAB辅助设计，仿真设计结果，主要的设计流程和步骤为：

(1)利用[N,WC]=buttord(Wp,Ws,Rp,As) 函数，根据设计指标确定模拟低通滤波器的阶次N及截止频率WC；

(2)利用[BS,AS]=butter(N,WC) 函数，创建模拟低通滤波器原型，得到模拟滤波器系统函数分子、分母系数向量BS和AS；

(3)利用[B,A]=lp2bs(BS,AS,WC,B) 函数，将模拟低通滤波器转换为中心频率为WC、带宽B为的模拟带阻滤波器；

(4)利用[Bz,Az]=impinvar(B,A,Fs) 函数，通过冲激响应不变法将模拟高通转化为数字带阻滤波器的系统函数分子、分母系数向量Bz和Az；

(5)利用[H,w]=frqze(Bz,Az)函数，得到数字滤波器频率响应。

设计结果如图1所示。由设计结果可知，利用“模拟-模拟频带变换”的方法通过冲激响应不变法完成模拟滤波器的数字化过程设计的带阻滤波器确实存在频谱混叠失真，不符合设计参数，达不到设计要求的。

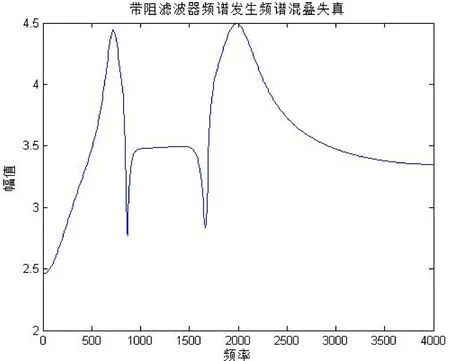
图1 模拟频带变换法设计数字带阻滤波器频谱图

为了消除频谱失真改变设计方法，利用“数字-数字频带变换”进行设计，其设计步骤为：

(1)将待求数字滤波器(DF)的设计指标转化为模拟低通滤波器(AF)的指标；

(4)利用数字频带变换将Hl(z)转化成待求带阻DF对应的系统函数H(z)。

由以上流程可知，“数字-数字频带变换”的实质就是从数字低通滤波器的Z平面映射到另一个待求所需类型数字滤波器的z平面的变化关系，关键点是找到Z到z的映射函数[3](318-321)Z-1=G(z-1)，则有H(z)=Hl(Z)|Z-1=G(z-1)。

设Z=ejθ，z=ejω，则数字低通映射为数字带阻的映射函数[3]为

其中

θp为数字低通滤波器通带截止频率，ωp1、ωp2为数字带阻滤波器通带截止频率。根据映射函数形式构建分子多项式N(z)和分母多项式D(z)，然后利用MATLAB程序自定义映射函数关系。

利用MATLAB辅助设计的设计流程和步骤为：

(1)利用[N,WC]=buttord(Wp,Ws,Rp,As) 函数，根据设计指标确定模拟低通滤波器的阶次N及截止频率WC；

(2)利用[BS,AS]=butter(N,WC) 函数，创建模拟低通滤波器原型，得到模拟滤波器系统函数分子、分母系数向量BS和AS；

(3)利用[Bz,Az]=impinvar(B,A,Fs) 函数，通过冲激响应不变法将模拟高通转化为数字带阻滤波器的系统函数分子、分母系数向量Bz和Az；

(4)自定义[bz,az]=mapping(Bz,Az,Nz,Dz)映射函数，求数字频带变换关系；

(5)调用mapping函数，将数字低通滤波器转换为数字带阻滤波器系统函数；

(6)利用[H,w]=frqze(Bz,Az)函数，得到数字滤波器频率响应。

其中自定义mapping函数为：

function[bz,az]=mapping(Bz,Az,Nz,Dz)

bzord=(length(Bz)-1); %原系统函数分子阶数

bzord1=(length(Bz)-1)*(length(Nz)-1); %变换后系统函数分子阶数

azord=(length(Az)-1); %原系统函数分母阶数

azord1=(length(Az)-1)*(length(Dz)-1); %变换后系统函数分母阶数

bz=zeros(1,bzord1+1); %分子系数向量初始化为0

for k=0:bzord %求各多项式乘积结果

pln=[1];

for l=0:k-1

pln=conv(pln,Nz); %求N(z)的k次乘积

end

pld=[1];

for l=0:bzord-k-1

pld=conv(pld,Dz); %求N(z)的bzord-k次乘积

end

bZZ=Bz(k+1)*conv(pln,pld);

bz=bz+Bz(k+1)*conv(pln,pld); %分子多项式系数向量求和

end

az=zeros(1,azord1+1)

for k=0:azord

pln=[1];

for l=0:k-1

pln=conv(pln,Nz);

end

pld=[1];

for l=0:azord-k-1

pld=conv(pld,Dz);

end

aZZ=Az(k+1)*conv(pln,pld);

az=az+Az(k+1)*conv(pln,pld); %分母多项式系数向量求和

end

az1=az(1);

az=az/az1;

bz=bz/az1;

构建映射函数，调用函数mapping()实现数字带阻滤波器，主要程序如下。

alpha=cos(p0);

klpha=(tan((P2-P1)/2))*(tan(Wc/2));

d1=-2*alpha/(1+klpha);

d2=(1-klpha)/(1+klpha);

Nz=[d2,d1,1];

Dz=[1,d1,d2];

[bz,az]=mapping(Bz,Az,Nz,Dz);

设计结果如图3所示。由频谱图可以看出，频率小于6kHz和大于14kHz的范围属于通带范围，在上通带频谱下降3dB的位置对应的频率大小约为5400kHz，接近于理论值。频率在8kHz和12kHz之间属于阻带，衰减大于20dB，完全满足设计要求。

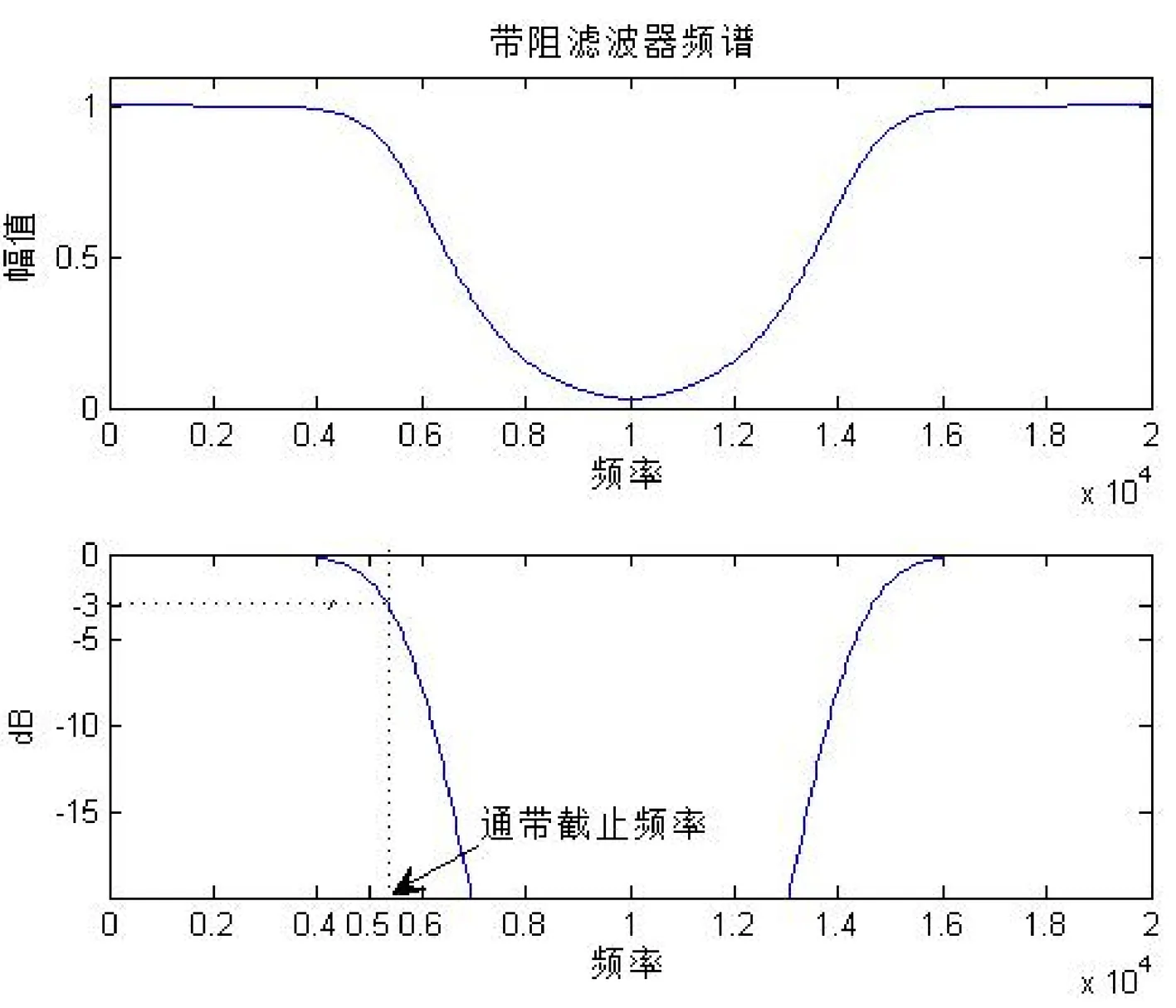
图2 消除频谱混叠失真的数字带阻滤波器频谱图

图3 数字带阻滤波器设计对比图

将利用“数字-数字频带变换”的方法实现的带阻滤波器的频谱与调用MATLAB中滤波器函数直接实现带阻滤波器的设计结果进行对比，频谱对比图如图3所示。由图可知，利用这两种方法进行设计的结果都基本能满足设计要求，在通带截止频率的对应上，“数字-数字频带变换”的方法对应截止频率约为5400kHz，直接发设计对应截止频率约为6800kHz，相比较而言前者设计方法误差更小，更接近设计指标。另外，使用“数字-数字频带变换”的方法设计的切贝雪夫Ⅰ型滤波器阶数为5阶，而直接实现的滤波器阶数为6阶，所以后者设计的滤波器在过渡带的范围内具有更陡的衰减特性，阻带的截止特性也更良好，但前者设计滤波器因为阶数少所以实际电路实现更简单经济、成本更低。

4 结果分析及结论

通过巴特沃斯数字带阻滤波器的设计实例可以看出，利用“数字-数字频带变换”设计的数字滤波器可以满足设计要求，仿真结果与理论计算值吻合度较高，验证了设计的正确性。并且在完成设计任务、实现设计指标的同时消除了由冲激响应不变法将模拟滤波器系统函数映射为数字滤波器的系统函数时带来的频谱混叠失真的问题，是一种有效的抗混叠的设计方法。