冲激响应时域测量电路设计与应用

田社平， 乔树通， 张 峰

（上海交通大学电子信息与电气工程学院，上海 200240）

0 引言

单位冲激响应反映了电路的性质。若已知电路的单位冲激响应，则可利用卷积积分的概念求解电路对任意激励的零状态响应［1-3］。在“电路理论”课程教学中，冲激响应、卷积积分皆被列为基本教学内容［4-5］。单位冲激响应是一人为定义的概念：单位冲激函数是理想的数学函数，在物理世界很难构造这一理想的函数。实际中很难直接通过实验直接测得（单位）冲激响应。在实际中，一些容易实现的信号，如（单位）阶跃激励、指数衰减激励、正弦激励等往往被用来作为电路的激励［6-7］。如何利用这些非冲激激励下的电路响应来计算电路的单位冲激响应，在理论上和实验中都是一个值得加以研究的问题［8］。

在复频域利用卷积定理可以容易计算单位冲激响应的拉氏变换。这一理论上简便的方法在实现时须借助数字信号处理技术，系统无论是经济成本还是复杂度都是比较高的。

本文提出一种冲激响应时域分析法，给出实现电路的设计方法。通过数值仿真和电路测试验证了该方法的正确性。冲激响应时域分析法具有物理含义明确，设计过程简明，实现成本低廉的特点。

1 单位冲激响应时域分析法

对任意单一激励的线性非时变动态系统，假设系统的激励为x（t）、响应为y（t），在单位冲激激励下的响应为h（t），则系统的响应和激励满足［9］

卷积积分是较为复杂的数学运算，直接由式（1）求解h（t）是比较困难的。为求解h（t），可引入一个中间函数来简化计算过程。假设该函数为g（t），将g（t）与式（1）两边进行卷积积分，得

令函数g（t）满足

则由式（2）不难得到

对于给定激励x（t）、响应y（t），如果能够找到满足式（3）的函数g（t），则由式（4）即可求得单位冲激响应h（t）。

利用卷积积分的性质，可求得常见激励函数所对应的函数g（t）。

例1阶跃激励Aε（t），其中A为比例系数。由式（3），函数g（t）满足

由卷积积分的微积分性质［9］，得

由式（6）可得

亦即

可见，g（t）等于一阶冲激偶函数除以一个比例系数。

例2指数衰减激励Ae-αtε（t）（α＞0）。由式（3），函数g（t）满足

直接求解g（t）较为困难。可利用下列两式间接求解。

由式（10）、（11）可得

可见，g（t）满足

例3正弦激励Acos（ωt）ε（t）。由式（3），函数g（t）满足

为求解g（t），先写出如下等式

由式（15）、（16）可得

可见，g（t）满足

类似地，可求出对应正弦激励Asin（ωt）ε（t）的g（t）函数

上述求解结果利用卷积定理不难加以验证。

2 冲激响应测量电路设计及其实验验证

以指数衰减激励为例讨论冲激响应测量电路的设计。假设系统的激励为x（t）=Ae-αtε（t）、响应为y（t），由上面讨论可知，系统的冲激响应

由式（20）可得测量系统实现框图如图1 所示。

图1 系统冲激响应测试图框

2.1 RC电路冲激响应的测量

RC电路是典型的一阶系统，针对RC电路，设计出如图2 所示的冲激响应测试电路，取电容电压作为电路的响应。测试电路包含跟随器、微分电路、加法电路、放大电路等，其中跟随器起隔离作用，加法电路采用反相电路，放大电路也采用反相电路［10-11］。RC电路的激励取x（t）=0.1e-0.2tε（t）V（见图2 中的元件ui）。

图2 一阶RC电路冲激响应测试电路

微分电路采用具有高输入阻抗的微分电路［10-12］，工作电路如图3 所示。由图可知，传递函数

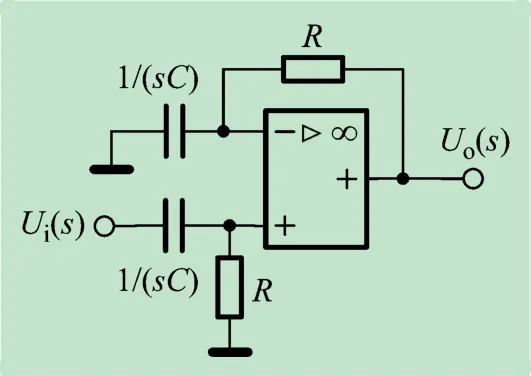
图3 微分电路工作原理

可见，电路的输入、输出关系为

亦即该电路对输入电压信号起到了微分的作用。按图2 所示电路元件参数，微分电路的R3=R4=100 kΩ，C2=C3=1 μF，可知RC=0.1，即微分电路在实现微分功能的同时，还对输入信号放大了0.1 倍。在反相加法电路，对微分输出信号又放大了10 倍（图中R5=2 kΩ，R6=20 kΩ）。

由于A=0.1，α=0.2，在反相加法电路，对RC电路的响应信号放大0.2 倍（R2=100 kΩ，R6=20 kΩ），在反相放大电路部分，其放大倍数为1/A=10（R9=10 kΩ，R10=100 kΩ）。

按图2 所示电路中RC电路的参数（R1=200 kΩ，C1=10 μF），可知，此RC电路的冲激响应为

为验证图2 电路的正确性，采用Multisim软件［13］进行实验仿真，仿真结果如图4 所示。由图可知，冲激响应仿真结果与冲激响应的理论结果几乎完全重合，初步验证了图2 电路的正确性。

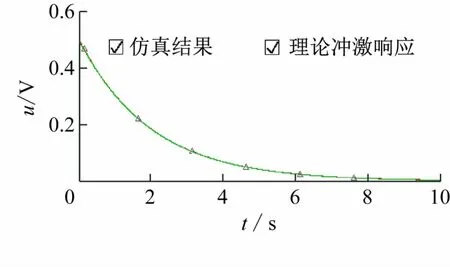
图4 RC电路冲激响应仿真结果

按图2 电路设计，搭建电路进行测量。采用AD713AQ四运放，该运放具有低输入偏置电流、输入失调电流和输入电压噪声。微分电路中的电容采用聚丙烯薄膜电容［14］。电路中所有电阻选用1/8W、1%金属膜电阻。激励信号通过数模转换系统自动生成。实测冲激响应结果如图5 所示。

图5 RC电路冲激响应实测结果

由图5 可知，所得结果与理论结果吻合，在响应的开始阶段，曲线上出现“毛刺”。产生这一现象的主要原因：

（1）激励信号通过数模转换系统产生，它不是理想的光滑曲线。

（2）微分电路中的运放、电容不是理想元件，当被微分信号变化较为剧烈时，电路会产生自激振荡，从而产生“毛刺”［15］。

事实上，对RC电路的电容电压响应进行分析，可求得电容电压响应

对式（24）两边求导，得

可见，在t=0 时刻，uC1（t）的变化率最大，随着时间的延长，其变化率逐步降低，自激振荡现象消失，响应曲线变得光滑。

2.2 RLC电路冲激响应的测量

RLC电路是典型的二阶系统，针对RLC电路，设计出如图6 所示的测试仿真电路，取电容电压作为电路的响应。电路参数分别取R1=1 Ω，L1=1 H，C1=1 F。电路的激励、测试电路部分与图2 电路相同。

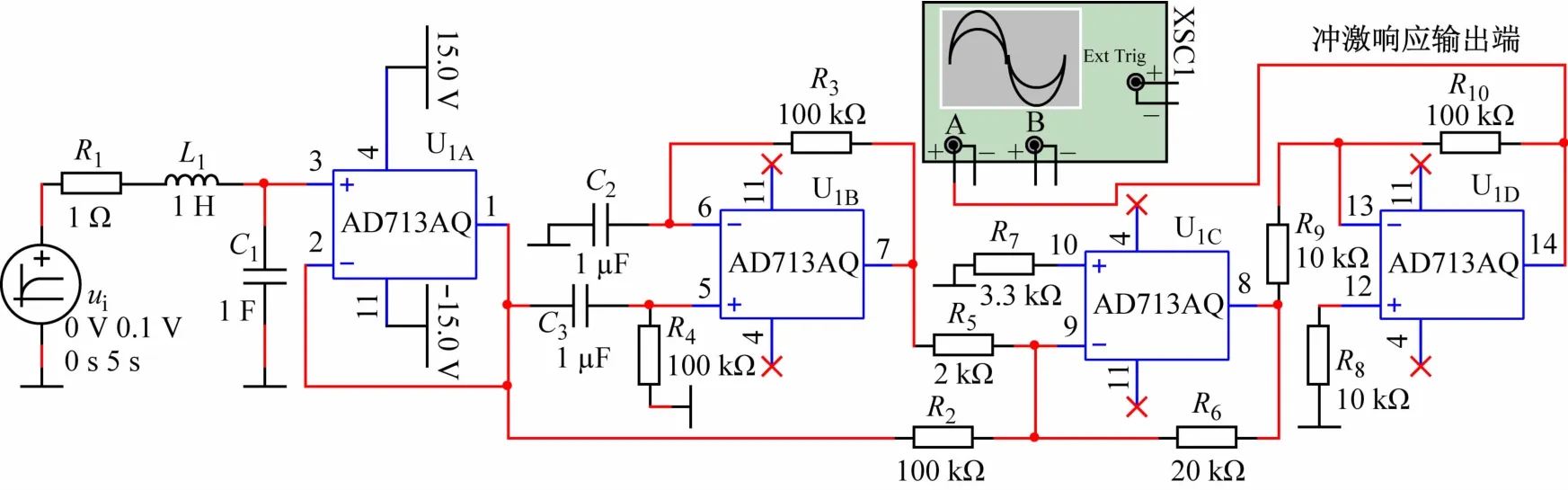
图6 RLC电路冲激响应测试电路

由RLC电路的元件参数，可求得电路冲激响应

采用Multisim软件对图6 电路进行实验仿真，仿真结果如图7 所示。由图7 可知，该结果与式（25）所示理论结果完全吻合。

图7 RLC电路冲激响应仿真结果

按照图6 电路的设计，搭建电路进行测量。取RLC电路的元件参数：R1=20 kΩ，L1=1 mH，C1=10 μF。经过理论分析，可求得电容C1的电压冲激响应

实测冲激响应结果如图8 所示。由图8 可知，所得结果与理论结果吻合。与一阶RC电路冲激响应测量结果类似，在响应的开始阶段，曲线上也有“毛刺”出现。“毛刺”产生的原因与上面分析类似。

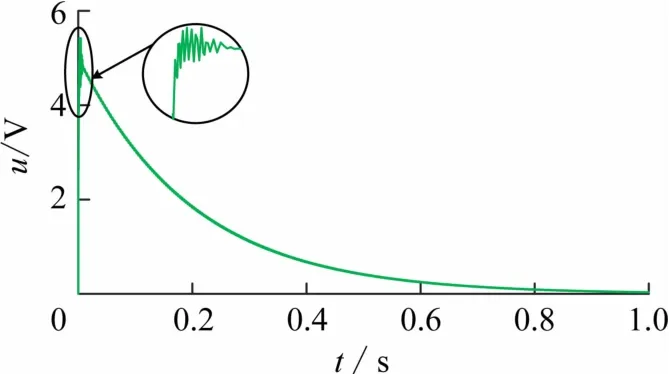
图8 RLC电路冲激响应实测结果

3 结语

基于卷积积分的概念和性质，提出一种电路冲激响应的时域分析方法。针对一、二阶电路设计冲激响应测量电路。实验、仿真结果表明，本文方法可以准确测量系统的冲激响应。

所提冲激响应测量方法实现了从时域直接对单位冲激响应的测量，概念简单，物理含义明确，且电路实现简单、成本低。