广义Sierpinski垫片及其推广形式的Hausdorff上测度的探究①

张元康， 齐 雪

(安徽科技学院信息与网络工程学院，安徽 凤阳 233100)

0 引 言

对于普通经典集合类和函数类的探究可使用微积分知识进行，但是对于一些非曲线的不规则集即分形的研究确实是很困难的，但它们却能更好地反映自然界万象。所以有必要研究自相似分形集合的Hausdorff测度与维数，但自相似分形集的Hausdorff测度与维数是很难精确求出的，即使自相似分形集的Hausdorff测度的上界估计都没有统一的说法，例如Sierpinski垫片的Hausdorff上测度的探究，文献[1～3]都做出过探究，文献[1]得出Sierpinski垫片的Hausdorff一个最大上界为：0.8701。文献[2]得出Sierpinski垫片的Hausdorff一个最大上界为：0.870031853。文献[3]得出Sierpinski垫片的Hausdorff一个最大上界为：0.8393。可以看出文献[3]的结果误差较大，而文献[2]的结果较为精确。而这也是可以理解的，同一个自相似分形利用不同的方法所得到的Hausdorff测度的上界是不一样的。文章先利用八边形覆盖的方法来探索一类广义Sierpinski垫片的Hausdorff测度上界的值，然后再将广义Sierpinski垫片试着进一步推广并探究其Hausdorff上测度，需要注意Sierpinski垫片有的文献里也称Sierpinski地毯。

1 广义Sierpinski垫片的形成

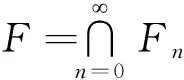
图1 自相似集合F的迭代过程

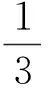
这是一种Hausdorff维数的近似估计方法，接下来视图探讨广义Sierpinski垫片F的Hausdorff上测度的估计方法。在此之前先介绍几个定理。

2 几个相关定理

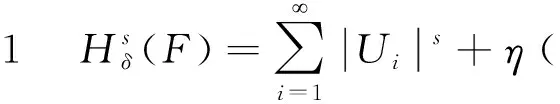
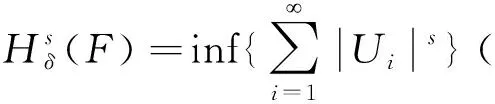
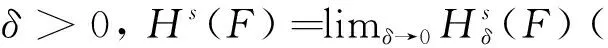
定理3Hs(F)引自文献[5])。

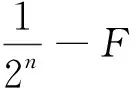
证明第一步假设D是闭集，D的补集记为Dc，故有F=(F∩D)∪(F∩Dc),从而推得,有

(1)

又因为Fi∩Fj的维数至多为1，所以

(2)

再由定理2可得:

(3)

且有：

(4)

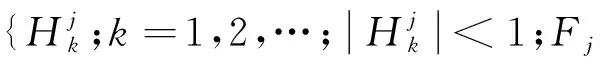
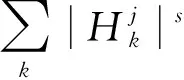
(5)

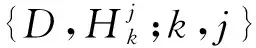
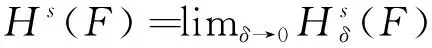
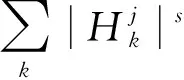
(6)

令(6)中的ε→0得：

Hs(D∩F)|U|s

(7)

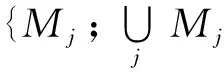
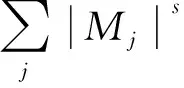
(8)

1

(9)

当Hs(F)>0时，令(9)式中的ε→0得：

(10)

又

(11)

联立(10)，(11)两式可得：

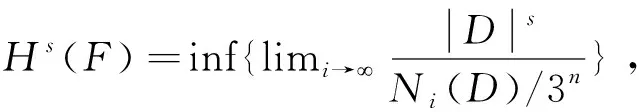
3 探究广义Sierpinski垫片F的Hausdorff上测度

结论1 广义Sierpinski垫片F的Hausdorff上测度的粗糙估计为Hs(F)1.6608。

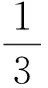
结论2 广义Sierpinski垫片F的Hausdorff上测度的近似估计为Hs(F)0.6481。

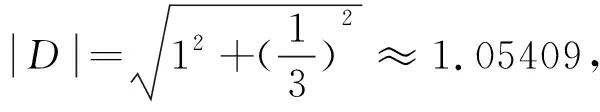
这个结果相比结论1的结果精确度更高。

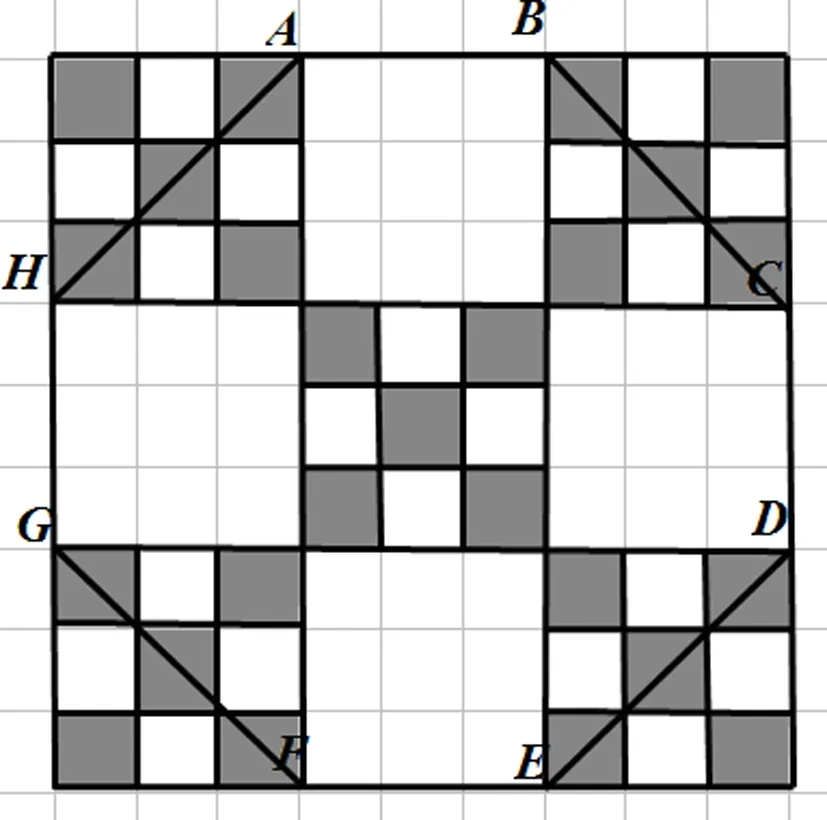
图2 Borel集合 D的选取方式)

4 广义Sierpinski垫片F的推广

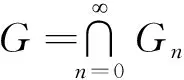
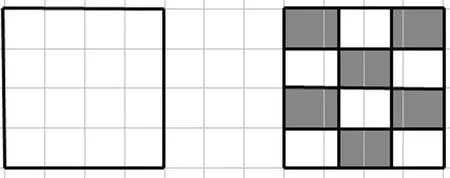
图3 自相似集合G的迭代过程

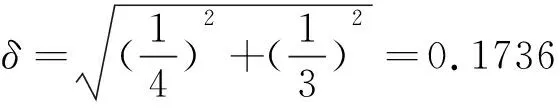
5 G的Hausdorff上测度估计

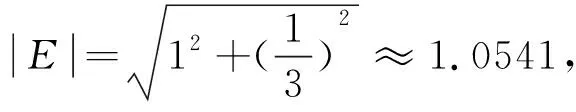
图4 Borel集合 E的选取方式

5 结 语

利用了八边形覆盖的方法探索了一类广义Sierpinski垫片的Hausdorff测度上界的值，然后再将广义Sierpinski垫片做了进一步推广并探究了其Hausdorff上测度，最后得到的数据比文献[3]的结论要更加精确。