“三学”视角下的习题课教学实践

包丽

“自学·议论·引导”教学法经过近四十年的不断完善、不断创新，已经成为特色鲜明、操作简便、效果明显的著名教学方式之一.其核心理念是教学应以学生为主体，在“师生”“生生”互动合作中使学生学会学习、学会思考，从而促成学生学力提升，最终实现学生自主发展.“自学·议论·引导”教学法的重要操作规则便是“三学”，即学材再建构、学法三结合、学程重生成.“三学”课堂应用广泛，适用于各种课型，本文以人教版八年级下册“平行四边形”中一道习题为例，解析“三学”视角下的習题课教学实践.

“平行四边形”是初中几何的重要章节，是在研究三角形、全等三角形、轴对称等基本图形之后的又一相对复杂的图形教学.在这一章节中，几何图形的定义、性质、判定等明显增多，针对书本知识，学生首先要熟练掌握定理，才能灵活运用.同样，本章的书本习题难度也有了明显提高.笔者以为，当一章节新课结束需要安排习题课时，教师应基于课后习题进行“学材再建构”，帮助学生进行深度学习.

一、基于知识点，夯实基础

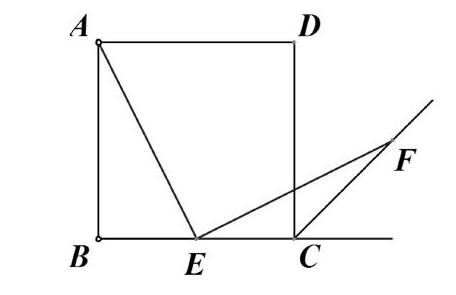
人教版八年级下册69页第14题：如下图，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90？紫，且EF交正方形外角的平分线于点F.求证：AE=EF.（提示：取AB的中点G，连接EG.）

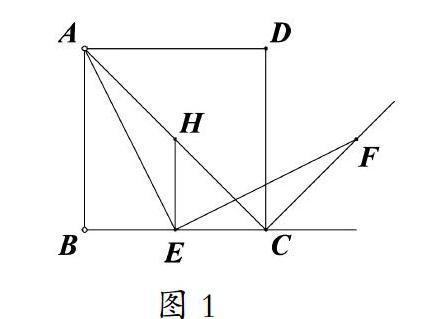
这是复习题中的一道高要求题，但题目本身有了提示，所以难度降低了不少，班级绝大部分学生是可以独立完成的。因此，在课前就可以让学生独立思考完成，课堂上让学生自主讲解.学生普遍能明白辅助线“取AB中点G，连接EG”的目的是要构造全等三角形，从而证明线段相等.用课本方法解决这道题以后，教师可以提出问题：“有没有其他构造全等三角形的方法呢？”通过分析，学生能够发现，要构造与△ECF全等的三角形，还可以作如图1所示的辅助线，过点E作BC的垂线，与AC交于点H，得到△AEH.

书本上的提示有时反而容易造成学生的思维定式，限制学生思考的宽度，所以教师要引导学生主动思考，努力寻找不同的解题路径。教师要利用好课本资源，为学生夯实基础.

二、学材再建构，变式训练

引导学生设想：原题中点E是BC的中点，如果点E是BC上任意一点，其他条件不变，结论是否仍然成立？

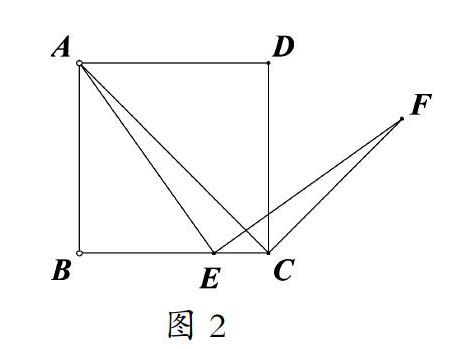
变式1 ：如图2，四边形ABCD是正方形，点E是边BC上的任意一点，∠AEF=90？紫，且EF交正方形外角的平分线于点F.求证：AE=EF.

有了刚才的分析，学生可以独立画图并找到解题路径.在此基础上，引导学生继续获得变式，获得新题目的过程，也是学生自主探究、合作学习的过程.

变式2：如图3，四边形ABCD是正方形，点E是边BC延长线上的任意一点，∠AEF=90？紫，且EF交正方形外角的平分线于点F.求证：AE=EF.

解决这个变式问题的方法和前面完全一致，可以在BA上取BG=CE，连接EG;也可以过点E作BC的垂线，与AC的延长线交于点H.

如果点E是CB延长线上一点，其他条件不变，是否仍然有这个结论呢？由此引出变式3.这种情况画图有一定的难度，要引导学生和原题对比，正确地画出图形.

变式3：如图4，四边形ABCD是正方形，点E是边CB延长线上的任意一点，∠AEF=90？紫，且EF交正方形外角的平分线所在直线于点F.求证：AE=EF.

与原题比较，如果用书上的方法解答，就是在AB的延长线上取点G，使BG=EB，连接EG，证明△AEG≌△EFC（如图5）;第二种方法即过E作BC的垂线，与CA延长线交于点H，证明△HAE≌△CFE（如图6）.

在课后习题解答基础上，得到三道变式训练题，通过将学材再建构，实现了学生的自主思考、交流研究，帮助学生寻找新方法解题的过程，让学生加深对常规方法的理解，最终使学生熟练掌握此类问题的解决方案.

三、学法三结合，掌握方法

教师继续提问：“如果这道题中的正方形变成菱形，可以得到什么样的题目？”

作为一堂常规习题课，要充分激发学生思维，设置足够的讨论辩解环节，习题量不宜过大，因此这些内容可以留作课后思考.课堂上学生解决了正方形中的四个问题，对课后的思考问题会有一定的兴趣.课后以个人学习、小组学习为主，到下一堂课再进行全班学习，将“学法三结合”融入整个数学活动.

变式4：如图7，四边形ABCD是菱形，∠B=60？紫，点E是边BC上的任意一点，∠AEF=60？紫，且EF交CD点F.求证：AE=EF.

这题是以菱形为背景的，如果题目变为“点E是等边△ABC的边上任意一点，∠AEF=60？紫且EF与△ABC外角平分线交于点F”，那么与原题就更相似了.在这里，重点是引导学生发现问题的本质，解决实际问题.

引导学生对应正方形问题的变式2和变式3，得到菱形背景下的变式5和变式6，如下.

变式5：如图8，四边形ABCD是菱形，∠B=60？紫，点E是边BC延长线上的任意一点，∠AEF=60？紫，且EF交直线CD于点F.求证：AE=EF.

变式6：如图9，四边形ABCD是菱形，∠B=60？紫，点E是边BC延长线上的任意一点，∠AEF=60？紫，且EF交直线CD于点F.求证：AE=EF.

在课堂研究的基础上，变式5和变式6都由学生自己叙述题目，自己画图，自主解答.学生会发现，这类问题都是相通的，也就不难找到解决问题的方法.

四、学程重生成，提升学力

在这堂习题课的教学过程中，充分进行了师生互动，生生互动，从而达到深度交流，自主建构.在习题课的教学中，我们要改变以下几种现象：一是只注重习题的“量”，而不注重习题的“质”.习题课如果只是由大量解答习题堆积而成，学生没有思考时间，只是被动接受，那么就没法通过充分交流来获得解题经验、解题方法.二是只重视“就题论题”的解题，而不注重“举一反三”的学力提升，由此，学生学不会灵活应用.在这堂习题课的教学中，笔者注重变式教学，引导学生深度思考，鼓励学生自己编题、画图分析，重视学程的生成，从而实现提高学力的目的.

“学材再建构，学法三结合，学程重生成”，这“三学”之间是相互联系、相互渗透的.学材再建构保证了教学内容的丰富，学法三结合保证了教学形式的多样，“三学”确保教学结构的活泼、教学氛围的民主、教学过程的完整.同时，学材再建构，学法三结合最终指向学程重生成，确保学生学力发展.

“三学”视角下的习题课实践，还有诸多方面需要改进提升，需要进一步深入研究，比如习题的选择、学材的建构、学法的运用，等等，都需要我们不断探索，在新形势下提升课堂效率，提高学生学习能力.

编辑/王一鸣 E-mail：51213148@qq.com