关于5D Schwarzschild-de Sitter黑弦时空的Nariai黑洞标量场方程的研究

张　晟，吴年祥，章　飞



关于5D Schwarzschild-de Sitter黑弦时空的Nariai黑洞标量场方程的研究

张晟1，*吴年祥1,2，章飞1

(1. 安徽国防科技职业学院电气技术学院，安徽，六安 237001；2. 六安市金安职业学校，安徽，六安 237011)

两个视界相互靠近的Nariai黑洞的研究在黑洞探索中是极其重要的。以5D Schwarzschild-de Sitter 黑弦时空离散的无质量标量场的演变为基础，利用Brevik 及Simonsen的方法可以将标量场方程作为引入实边界条件的边界值问题求解，然后用方形势垒代替5D的连续势垒，得到了反射系数（R）和透射系数(T)。

Nariai黑洞；无质量标量场；势垒；反射系数；透射系数

0 前言

Stephen Hawking用量子场的方法所证明的黑洞辐射存在，引发人们利用不同方法捕获黑洞的辐射粒子以便对黑洞进行深入研究。Higuchi 和Grispino等人[1]给出了Schwarzschild 黑洞之外标量场方程。Brady和Tian 等人[2]研究Schwarzschild-de-Sitter (SdS). Guo[3]进一步研究了Reissner- Nordstrom-de Sitter的情况。

Kaluza和Klein提出了世界高于四维的思路，使统一普通相对论和电磁场的Maxwell理论成为可能。于是，高维空间研究成了热点。本文主要考虑由Wesson及其合作者提出的时空物质理论（STM）。因其非紧凑第五维度而有别于经典的Kaluza-Klein理论，并认为四维的来源是由空的五维流形所引起。Campbell定理从数学上给予了支持，即任何多维的有源的爱因斯坦方程解析解可以局部地嵌入到（N+1）维度Ricci-flat流形[4]中，其相关成果可见参考文献[5]。

1 5D Schwarzschild-de Sitter黒弦时空中的无质量标量场

在STM理论下，由Wesson 等人所提出的精确的5D解描述了5D黑洞[8]，线元形式如下：

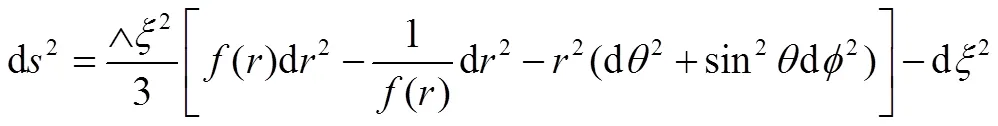
重新定义第五维度

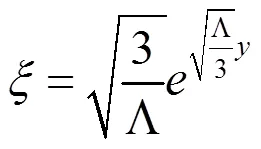
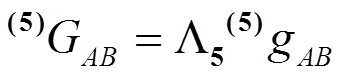
在重新定义第五维度后,度量标准可以转换为

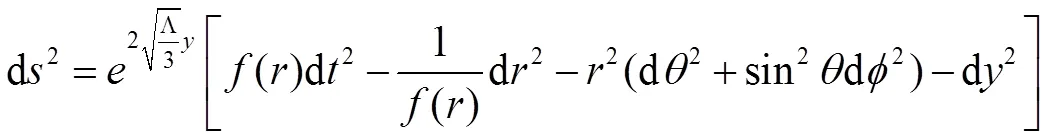
其中y是新的第五维度。式（2）可以改写为

5D黒弦时空里的无质量标量场也遵循Klein-Gordon方程

2 Nariai黑洞及其边值问题

2.1 第五维函数

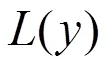
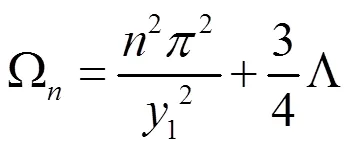
图1　Nariai中的前两个特征函数Ln(y)图：L1(实线)，L2（虚线）(Λ＝，C＝y1→1)

2.2 类Schrödinger波方程

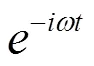
乌龟坐标

将（2）式代入上式积分可得乌龟坐标为：

式中

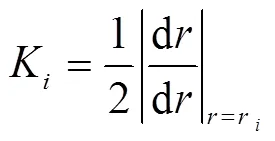
由此可得：

所以，在乌龟坐标（17）形势下，径向方程（15）可以写成

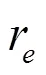
2.3　数值解

所以方程（21）变为：

作为两个视界（6）附近的边界条件。

综合边界条件（27）式和正切近似（26）式，可用数学软件得到方程（21）式的数值解。

图3 波振幅与乌龟坐标x的关系图(M=1,Λ＝，l=1, y1=10,n＝1)

图4 波振幅与r关系图(M=1,Λ＝,l=1, y1=10,n＝1)

2.4 反射和透射

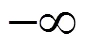
考虑势垒隧穿效应，方程（21）的解为：

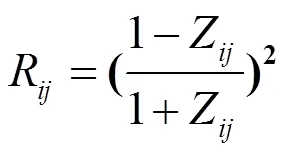
=1(实线),=2(虚线), 4Dcase (虚点线)

图6 logR与高度H关系图(d=40,M=1,Λ＝，l=1, y1=10)

3 结论

本文求解了5D SDS黑弦时空中的Nariai黑洞实标量场方程,并得到其反射系数和透射系数。

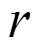
[1] Higuchi A, Matsasand G E A. Sudarsky[J]. Physical Review D, 1998 , 58(1):104-115 .

[2] Crispino L C B, Higuchiand G E A. Matsas[J]. Class and Quantum Gravity,2000,17(4):17-19.

[3] Barrau A, Boudoul G, Donato F, ea tl. P. Salati,I.Stefanon and R.Taillet[J].Annual Review of Astronomy and Astrophysics,2003,20(14):398-403.

[4] Campbell J E. A Course of Dierential Geometry[M]. A.Billyard,P. S.Wesson and D.Kalligas.Massachusetts: International Journal of Modern Physics D Publisher ,1995:639-645.

[5] Liu H Y, Wesson P S. Reconstruction of 5D Cosmological Models from the Equation of State of Dark Energy[J].Physics Letters B ,1996,20(6):381-420.

[6] Kanti P, Panagiota. Black Holes in Theories with Large Extra Dimensions[J].International Journal of Modern Physics A ,2004,19(29):4899-4951.

[7] 孙孟.黑弦流及其热力学涨落[D].北京:北京工业大学, 2015

[8] 徐嵩. 转动探针D3膜等对全息Schwinger效应势能的研究[D]. 北京:北京工业大学, 2016

[9] 李彩凤.腔量子电动力学中的自旋压缩问题研究[D]. 太原:山西大学, 2016.

ON THE STUDY OF NARIAI BLACK HOLE SCALAR FIELD EQUATION IN THE 5D SCHWARZSCHILD-DE SITTER BLACK STRING SPACE

ZHANG Sheng1,*WU Nian-xiang1,2, ZHANG Fei1

(1. School of Electrical Engineering ,Anhui National Defense Vocational College,Luan,Anhui,237001; 2. LuAnShi JinAn Vocational School,Luan,Anhui,237011)

In the research of black hole, it is of great importance to study Nariai black hole which has two horizons close to each other. We tend to study the revolution of a massless scalar field scattered by 5D Schwarzschild-de Sitter black string space. Furthermore, we use the methods of Brevik and Simonsen to solve the boundary value problem with the scalar field equation as real boundary condition. Finally, we employ square barrier instead of 5D continuous potential and works out the reflection conflicts (R) and transmission conflicts (T).

Nariai black hole;massless scalar field;potential;reflection conflicts;transmission conflicts

1674-8085(2018)05-0027-06

P145.8

A

10.3969/j.issn.1674-8085.2018.05.006

2018-02-01；

2018-08-21

安徽省教育厅自然科学基金重点项目(KJ2017A777,KJ2015A438 )；2017安徽省高校优秀拔尖人才培育（gfxy2017187)；安徽省质量工程项目（2017jyxm0770,2017jyxm0772,2017kfk165）；安徽国防科技职业学院质量工程项目（gf2016jxyj205,,gf2017 zyzy02，gf2017 jpkc13,gf2017jpkc14 ）。

张 晟(1968-),男，安徽六安人，讲师/工程师，,主要从事磁场、电力电子技术研究(E-Mail:jiezhengsheng@163.com)；

*吴年祥(1984-),男，安徽安庆人，高级实验师,硕士,主要从事模式识别与智能控制研究(E-Mail:ahgfwnx@163.com)；

章 飞(1982-),男，安徽安庆人，讲师，硕士,主要从事数字信号处理研究(E-Mail:philex_hf@163.com).