渐近拟非扩张映射三步混合迭代算法的收敛性

刘涌泉，杨　旭，谢　涛



渐近拟非扩张映射三步混合迭代算法的收敛性

*刘涌泉1，杨旭1，谢涛2

（1．吉安职业技术学院师范学院，江西，吉安 343000；2. 常州卫生高等职业技术学校文化基础部，江苏，常州 213000）

本文引入了关于三个渐近拟非扩张自映射和三个渐近拟非扩张非自映射新的三步混合迭代算法，在实Banach空间中，获得了渐近拟非扩张自映射和渐近拟非扩张非自映射在新的三步混合迭代算法下的强收敛的充分必要条件，所得结果推广和改进了许多相关文献的结论。

公共不动点; Banach空间; 三步迭代; 渐近拟非扩张自映射; 渐近拟非扩张非自映射

1 预备知识

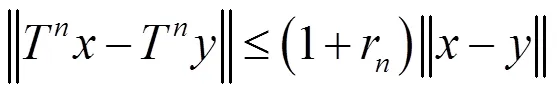
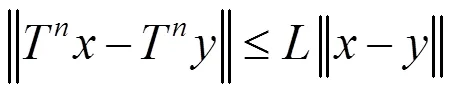
注1 （Ⅰ）非扩张映射必是拟非扩张映射，同时也是渐近非扩张映射；（Ⅱ）渐近非扩张映射一定是渐近拟非扩张映射，同时也是一致-Lipschitzian映射；（Ⅲ）一致-Lipschitzian映射必定是一致(,)-Lipschitzian映射。反之，（Ⅰ）（Ⅱ）、（Ⅲ）一般都不成立。

2003年，Chidume等人[1]引入了渐近非扩张非自映射的概念。

注2 （Ⅰ）渐近非扩张非自映射必是一致(,1)-Lipschitzian非自映射，同时必定是渐近拟非扩张非自映射；（Ⅱ）一致(,1)-Lipschitzian自映射也被称为一致-Lipschitzian映射。

2003年，Childume 等人[1]在一致凸Banach空间中，通过研究下面的迭代（Mann迭代）

2006年，Wang[4]将迭代（1）推广到了渐近非扩张非自映射的Ishikawa迭代。后来，Thianwan[5]考虑了一种新型的迭代方法（投影型Ishikawa迭代）如下：

2012年，阚绪周等人[6]一致凸Banach空间中引入了三步迭代算法：

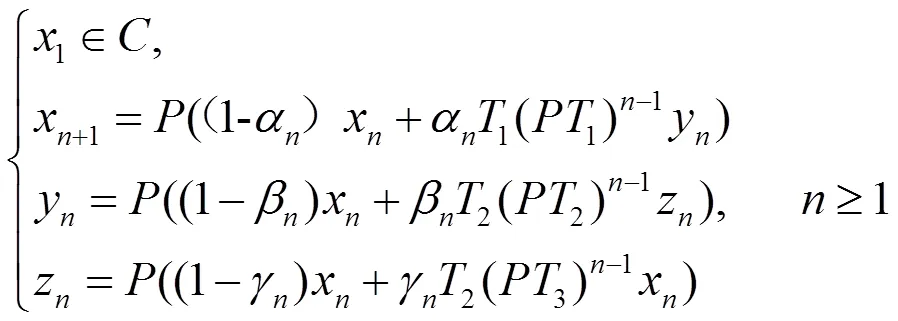
2018年，刘涌泉等人[7]在实Banach 空间中，引入了两个渐近拟非扩张自映射和两个渐近拟非扩张非自映射带误差的混合迭代序列：

本文的结果是一些作者相应结果的重要推广，参见文献[7-16]。为了证明本文的主要定理，需要引入以下重要引理。

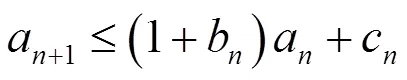
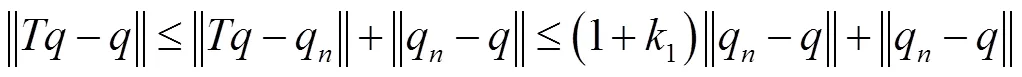
2 主要结果

本部分目的是在一般实Banach空间中，证明三个渐近拟非扩张自映射和三个渐近拟非扩张非自映射关于迭代序列（6）的强收敛性的充分必要条件。

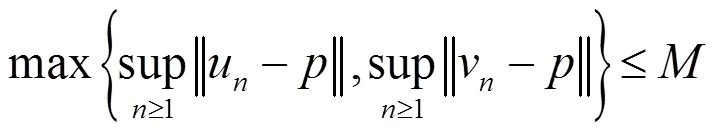
由（6）知

由式（7）可知，

且

将式（8）代入式（9）得到

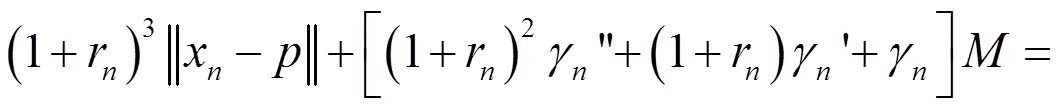
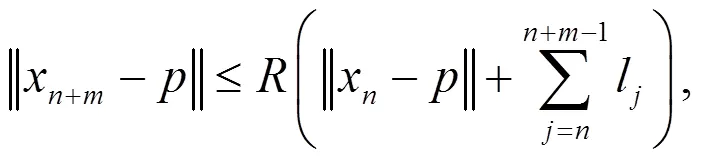
证明由引理2.1可知

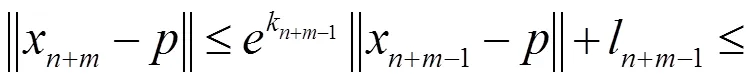
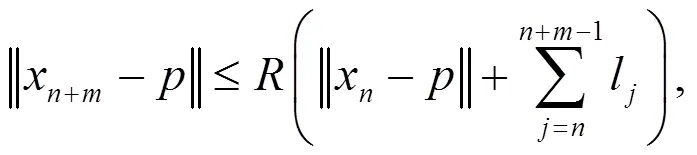
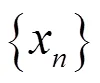
故

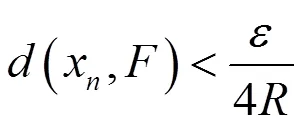
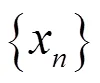
证明注意到

由定理2.1可知，定理2.2成立。证毕。

[1] Chidume C E, Ofoedu E U, Zegeye H. Strong and weak convergence theorems for asymptotically nonexpansive mappings [J]. Journal of Mathematical Analysis and Applications,2003,280(2):364-374.

[2] 刘涌泉,郭伟平. 混合型渐近非扩张映射合成隐迭代序列的收敛性定理[J].数学物理学报,2015,35(2):422-440.

[3] Wang C, Zhu J, An L. New iterative schemes for asymptotically quasi-nonexpansive nonself-mappings in Banach spaces [J]. Journal of Computational and Applied Mathematics, 2010,233 (11): 2948-2955.

[4] Wang L. Strong and weak convergence theorems for common fixed points of nonself asymptotically nonexpansive mappings [J]. Journal of Mathematical Analysis and Applications, 2006,323(1):550-557.

[5] Osilike M O, Aniagbosor S C. Weak and strong convergence theorems for fixed points of nonexpansive mappings[J]. Mathematical and Computer Modelling, 2000,32(10): 1181-1191.

[6] 阚绪周,郭伟平. 渐近非扩张非自映射的收敛定理(英文)[J].应用数学,2012,25(3):638-647.

[7] 刘涌泉,黄星,饶永生. 渐近拟非扩张映射的新型混合迭代算法及应用[J].哈尔滨师范大学:自然科学学报,2018, 34(1):15-21.

[8] Thianwan S. Common fixed points of new iterations for two asymptotically nonexpansive nonself-mappings in a Banach space [J]. Journal of Computational and Applied Mathematics, 2009,224 (2): 688-695.

[9] Shahzad N, Udomene A. Approximating common fixed points of two asymptotically quasi-nonexpansive mappings in Banach spaces[J]. Tamkang Journal of Mathematics,2006,42(1):19-30.

[10] 冯先智,倪仁兴. 渐近非扩张的非自映象不动点的迭代逼近问题[J]. 数学杂志,2009,29(1):87-92.

[11] Yildirim I, Ozdemir M. Approximating common fixed points of two asymptotically quasi-nonexpansive mappings in Banach spaces[J]. Tamkang Journal of Mathematics, 2011,42(1): 19-30.

[12] 沈德兄,郭伟平. 渐近拟非扩张非自映射的收敛定理[J].纯粹数学与应用数学,2016,32(1): 100-110.

[13] Liu Q. Iterative sequence for asymptotically quasi- nonexpansive mappings with error member[J]. Journal of Mathematical Analysis and Applications, 2001,259(1): 18-24.

[14] Weng X. Fixed point iteration for local strictly pseudo-contractive mapping[J]. Proceedings of the American Mathematical Society, 1991,113(3):727-731.

[15] 张学茂. 渐近非扩张映像隐式迭代序列强收敛性[J].湖北民族学院学报:自然科学版, 2015,33(1):22-24.

[16] 李智,崔云安,张新. 渐近拟非扩张映射的三步迭代序列的收敛定理[J].哈尔滨商业大学学报:自然科学版,2009, 25(2):234-236.

THE CONVERGENCE OF A NEW THREE-STEP MIXED ITERATIVE SCHEME FOR ASYMPTOTICALLY QUASI-NONEXPANSIVE MAPPINGS

*LIU Yong-quan1, YANG Xu1, XIE Tao2

（1.Normal School, Ji’an College, Ji’an, Jiangxi 343000, China； 2. Department of Cultural Foundation, Changzhou Hygiene Vocational Technology College, Changzhou,Jiangsu 213002, China）

A new three-step mixed iterative scheme for three asymptotically quasi-nonexpansive self-mappings and three asymptotically quasi-nonexpansive nonself-mappings is introduced. Several convergence theorems are established in real Banach spaces. Our results improve and extend the results announced by many others.

common fixed point; Banach space; three-step iterative scheme; asymptotically quasi-nonexpansive self-mappings; asymptotically quasi-nonexpansive nonself-mappings

1674-8085(2018)05-0007-06

O177.91

A

10.3969/j.issn.1674-8085.2018.05.002

2018-06-30；

2018-08-24

吉安职业技术学院教研项目（16JY135）

*刘涌泉(1987-)，男，江西高安人，助教，硕士，主要从事非线性泛函分析研究(E-mail:1597966abc@163.com);

杨旭(1988-)，男，江西赣州人，讲师，硕士，主要从事数学教育研究研究(E-mail:627989875@qq.com);

谢涛(1986-)，男，江西常州人，讲师，硕士，主要从事非线性泛函分析研究(E-mail:858507287@qq.com).