Gorenstein范畴的一个推广

何东林，李煜彦



Gorenstein范畴的一个推广

*何东林，李煜彦

(陇南师范高等专科学校数信学院，甘肃，陇南 742500)

主要介绍并研究强W-Gorenstein范畴SG(W)。进而证明了是W-Gorenstein范畴中的对象当且仅当是强W-Gorenstein范畴SG(W)中对象的直和因子。

强W-Gorenstein范畴；正交；Abel范畴；直和因子

1 预备知识

设 A是Abel范畴。本文中的子范畴均指加法全子范畴，即关于同构、有限直和及直和因子封闭的子范畴。Auslander 在文献[1]中介绍了双边Nother环上有限生成模的G-维数。

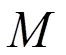
先介绍几个定义。

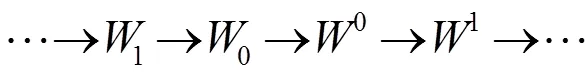
注：设R为有单位元的结合环。

[1]当W= P(R)时，W-Gorenstein对象就是Gorenstein投射模。

[2]当W= I(R)时，W-Gorenstein对象就是Gorenstein内射模。

在上面定义的基础上，受文献[4]的启发，我们引入强W-Gorenstein对象的概念。

定义2 称A中对象M是强W-Gorenstein对象，如果存在正合列

A中所有强W-Gorenstein对象组成的子范畴，记作SG(W) 。

注：[1] 当W= P(R)时，强 W-Gorenstein对象就是强Gorenstein投射模。

[2] 当W= I(R)时，强W-Gorenstein对象就是强Gorenstein内射模。

[3] 强W-Gorenstein对象一定是W-Gorenstein对象。

2 主要结论

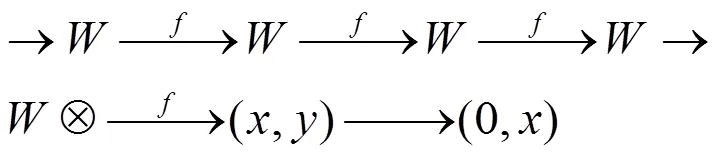
考虑如下交换图

证明 设G(=1,2,…,)是强W-Gorenstein对象，则存在正合列

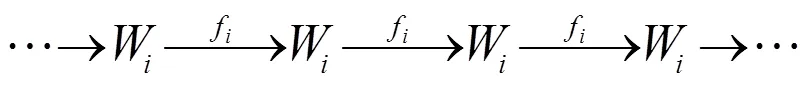
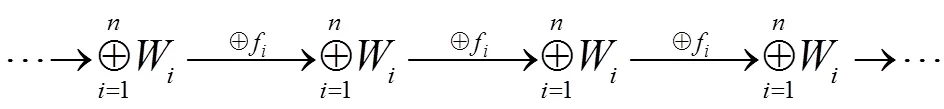
考虑如下交换图

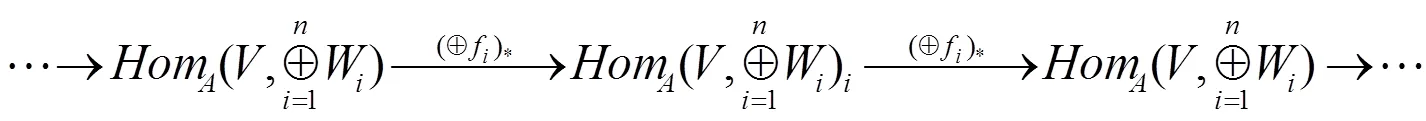
由命题2的证明过程及直和的性质易得如下结论。

推论1如果W关于任意直和封闭，那么SG(W)也关于任意直和封闭。

引理1如果W自正交，那么G(W)关于扩张及直和因子封闭。

证明 由文献[5]中推论4.5和命题4.11易知。

下文中均假设W自正交。

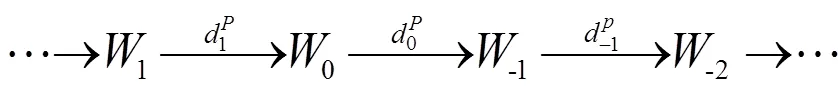
考虑交换图

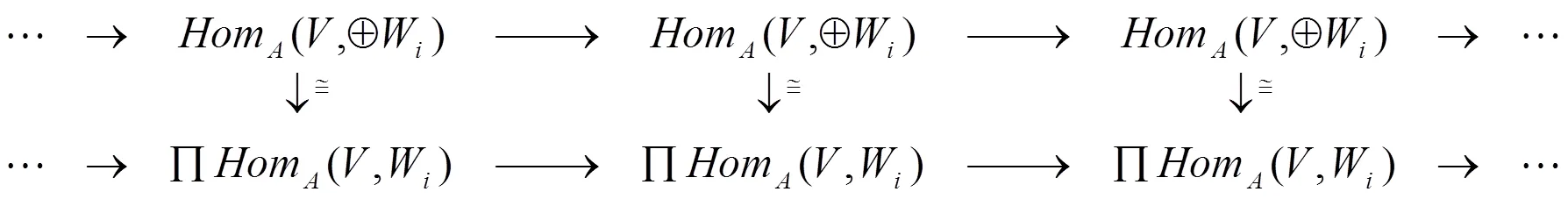
和

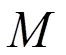
下面给出强W-Gorenstein对象的若干等价刻画。

正合；

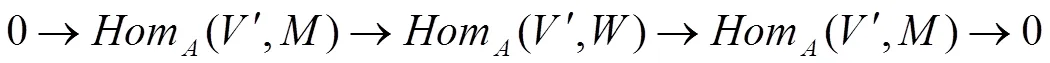
和

正合。

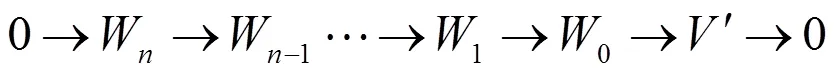
和

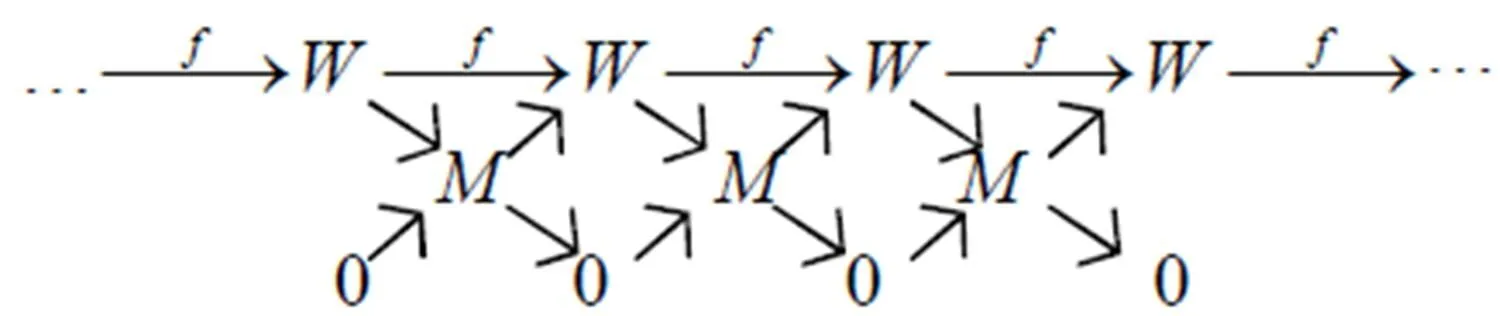
由此定理，考虑到投射模的特殊性，易知如下结论。

[1] Auslander M, Bridger M. Stable Module Theory. Memoirs of the American Mathematical Society[J]. 1969,94:Providence, RI: American Mathematical Society.

[2] Enochs E E, Jenda O M G. Gorenstein injective and projective modules[J]. Math Z, 1995,220:3225-3237 .

[3] Holm H. Gorenstein homological dimension[J]. J Pure Appl Algebra, 2004,189:167-193.

[4] Bennis D, Mahdou N. Strongly Gorenstein projective, injective and flat modules[J].J. Pure Appl. Algebra, 2007,210: 437-445.

[5] Sather-Wagstaff S, Sharif T, White D. Stability of Gorenstein categories[J]. J London Math Soc., 2008,77: 481-502.

[6] Zhao G Q, Sun J X.-Gorenstein categories[J]. Turk J Math, 2016, 40: 365-375.

[7] Enochs E E, Jenda O M G. Relative homological algebra [M]. New York:Walter de Gruyter,2000.

[8] Anderson F W, Fuller K R. Rings and categories of modules [M].New York: Spring Verlag,1992.

[9] Yassemi S. Gorenstein dimensions.[J] Math. Scand. 1995, 77:161-174.

[10] 佟文廷. 同调代数引论[M].北京：高等教育出版社, 1996.

A GENERALIZATION OF GORENSTEIN CATEGORY

*HE Dong-lin, LI Yu-yan

(Department of Mathematics, Longnan Teachers College, Longnan, Gansu 742500, China)

We introduce and investigate the strongly W-Gorenstein category SG(W). Furthermore we prove thatis an object of the W-Gorenstein category G(W) if and only ifis a direct summand of strongly W-Gorenstein category SG(W).

strongly W-Gorenstein category; self orthogonal; ablian category; direct summand

1674-8085(2018)05-0017-05

O153

A

10.3969/j.issn.1674-8085.2018.05.004

2018-06-01；

2018-08-04

甘肃省高等学校科研项目（2018A-269）

*何东林(1983-)，女，甘肃白银人，讲师，硕士，主要从事同调代数研究(E-mail: hdl7979085@163.com);

李煜彦(1983-)，男，甘肃西和人，讲师，硕士，主要从事环模理论研究(E-mail:nwnulyy@126.com).