一种灵活的椭圆曲线密码并行化方法
2018-03-13邬可可黄国伟孔令晶
邬可可,黄国伟,孔令晶
(深圳信息职业技术学院计算机学院,广东 深圳 518172)
0 引 言
1980年代中期,Miller[1]和Koblitz[2]分别独立地提出了椭圆曲线密码体制(Elliptic Curve Cryptosystems, ECC)。相对于其它的公钥密码体制,ECC只需较短的私钥就可以达到较高的安全级别,所以,近年来ECC受到广泛关注。在ECC中,标量乘dP是最主要且最耗时的操作。通常,标量乘采用逐比特的二进制方法来计算[3]。给定一个标量d和一个椭圆曲线点P,一个标量乘是由一系列的P点的点加(A)和点倍(D)操作完成,其运行的轨迹依赖于标量d的二进制比特表达式。该标量乘结构包括3个操作级别:标量乘的算法级别、点的算术级别和域的算术级别。本文专注于使用标量乘的算法级别来加速标量乘的计算。由于逐比特的串行操作,使得它的操作时间相对较长,对于标量d(比特长度为k),二进制方法的时间复杂度达到了(k/2)A+kD。为进一步加速标量乘,各类二进制方法的变形相继被提出,如各类快速的标量乘方法如NAF方法、窗口NAF方法,以及滑动窗口方法等[4]。
然而,这些串行的标量乘方法已不能适应于日益普及的高性能并行计算系统。为适应高性能系统,并行的标量乘方法是迫切需要的,一些并行的标量乘方法也被提出。文献[5-6]介绍了基于SIMD处理器结构的高效并行点操作,基于2个或3个并行操作,采用改进的雅可比坐标(X,Y,Z,Z2)来开发快速并行表达式。文献[7-8]提出了双处理器架构的表达式。文献[9-12]介绍了替换乘方法,它允许更高效的优先并行操作的开发,从而能并行执行3个或4个操作的快速并行表达式。文献[13-17]提出了基于点操作的算术级别的并行化,但只适用于2个处理器并行化处理点加和点倍操作。然而,这些方法依赖于点或域的算术级别,只局限于域上的固定数量的平方和乘的并行化,即指令级别并行化,而不是基于任务级别的划分,故它们大多只能用于固定少数处理器的并行计算系统(通常为2,3或4个处理器的并行处理器系统),因而难以适用于日益普及的大型并行系统。
本文划分一个任务(标量乘)为若干个相同类型的子任务(子标量乘),直到这些子问题分布到并行系统的处理器;然后,将这些子问题的解递归地整合成原始问题的解。任务的划分是灵活闭包的,因此,本文提出的并行标量乘方法是灵活的且基于任务级别的并行化(也就是标量乘算法操作级别并行化),从而能适用于各种规模的并行计算系统,而不局限于固定数量的处理器。
1 背 景
计算标量乘dP最常用的是经典的二进制方法[3-4],它是基于标量的二进制展开式d=(dkdk-1…d2d1)2,其中dk是最高有效位(MSB),d1是最低有效位(LSB),k是标量的比特数(即标量长度)。二进制方法有2种实现版本,一种是从标量的LSB到MSB扫描标量,另一种是从标量的MSB到LSB扫描标量,例如后者的计算过程如下:
算法1Binary Method
输入:d=(dkdk-1…d2d1), P∈E(Fq)
输出:dP
Q=O;
for i from k to 1 do /*从 MSB到LSB扫描d */
{
Q=2Q; /*DBL*/
if(di=1) then Q=Q+P; /*ADD*/
}
return(Q);
在二进制比特串d中,di=1的概率为50%,也就是算法1以50%的概率执行点加操作{Q=Q+P;},也就是大约k/2次的ADD操作加上k次的DBL操作,记为(k/2)A+kD。
2 提出的划分与整合模型
在对本文的技术方案作进一步说明之前,首先给出如下的划分与整合模型:
定义1设x,y是正整数,|y|表示y的二进制比特长度。定义如下函数:
f(x,y)=2(|y|)·x+y
(1)
根据定义1,很容易得出如下引理。

(2)

(3)
为了更好地描述从各个子标量乘整合成最终标量乘的计算过程,根据引理1,可以推导出如下的定理:

(4)

证明:根据定义1和引理1,有如下等式成立:
(5)
在等式(5)的等号两边都乘以一个任意的椭圆曲线点P,可以推导出如下的等式成立:
(6)
根据定理1,可以递归地并行计算2n个椭圆曲线点的每2个相邻点加,直到计算最后2个点的点加运算。
3 提出的并行化方法
首先根据划分与整合模型,给出标量乘并行化的步骤,最后给出一种灵活的并行化标量乘方法。
3.1 并行化步骤
基于上述划分与整合模型,标量乘并行化步骤如下:

d=(dkdk-1…d2d1)2
(7)
2)由此标量乘dP被划分成2n个子标量乘,且这些子标量乘可由二进制方法实现,划分的过程如下:


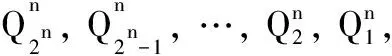
(8)

3)两两递归地计算这2n个椭圆曲线点的点加,直到计算最后2个点的点加,这个过程叫椭圆曲线点的整合过程。根据定理1,这2n个椭圆曲线点的整合过程为:

…
(9)
整合过程如图2所示。

图2 椭圆曲线点的整合过程
3.2 并行化方法
根据划分与整合的并行化步骤,给出一种灵活的标量乘并行化方法,其算法描述如下:
算法2灵活的标量乘并行化方法

输出:dP
1) Q=O;
2) for j=1 to 2ndo in parallel
3) {/*调用二进制方法计算子标量乘*/
}
4) for i=n-1 downto 0 do
for j=2i+1downto 2 by 2 do in parallel
该方法是划分一个任务(标量乘)为若干个相同类型的子任务(子标量乘),直到这些子问题分布到并行系统的各个处理器。然后,这些子问题的解被递归地整合成原始问题的解。任务的划分是灵活闭包的,因此,本文提出的并行标量乘方法是灵活的且基于任务级别的并行化(也就是标量乘算法操作级别并行化),从而能适用于各种规模的并行计算系统。
4 复杂度分析

(10)

(11)
既然标量d的比特长度k在一个加密解密环境中是不变的,那么tp的最小值只取决于标量折半的次数n。根据等式(11)中的项(k/2n+1+n),定义如下函数:
(12)
对x求g(x)偏导数如下:
(13)
当g′(x)=0,也即x=log k+log (ln 2)-1时,g(x)取得最小值。因此,当x
(14)
为简单起见,本文取最优折半次数nopt=log k-2。因此,可以根据并行计算系统的处理器的数量,来选定最优的n值。
当一个并行系统的可利用处理器的数量不少于2n=2log k-2=k/4,得到最优的折半次数n=log k-2。根据处理器的数量,给出该算法的时间复杂度tp如下:
(15)
其中p(等于2n)为一个并行系统的可利用处理器的数量。当并行处理器数量p较多时,该算法的时间复杂度远小于二进制方法的(k/2)A+kD。
例如,如果标量d的比特长度k=256,那么最优的折半次数n=log2256-2=6。当p<26时,应该折半标量log2p次,以获得最优的时间复杂度为tpmin=(256/2p+log p)A+256D。然而当p≥26时,应该折半标量6次,以获得最优的时间复杂度tpmin=8A+256D,比经典的二进制方法的128A+256D减少了大约30%的时间复杂度。
5 实例应用
本实例描述本文的快速灵活的标量乘方法的并行化过程。为简单起见,不妨假设标量d=(38749)10=(1001011101011101)2,则标量d的比特长度为k=16。
5.1 划分与整合模型
根据等式(14),最优的折半次数nopt=log 16-2=2,则折半标量为2次,如图3所示。

图3 折半划分标量2次
根据引理1,在这4个子标量中两两递归并行整合子标量,直到整合最后2个子标量为初始的标量d。标量整合模型如图4所示。
5.2 并行化过程
基于标量折半模型,标量乘dP=38749P能被划分为4个子标量乘,这4个子标量乘能被并行地调用二进制方法来计算。如下式所示:

(16)
通过调用二进制方法来计算4个子标量乘,得到4个椭圆曲线点的并行输出。
根据定理1,递归并行地计算着4个椭圆曲线点中的每2个点的点加,直到只需计算最后2个点的点加。标量乘dP=38749P的并行化过程如图5所示。

图5 标量乘的并行化过程

根据等式(14),最优的时间复杂度为tp=16D+4A。然而,串行的二进制方法达到ts=16D+8A。
6 算法比较
与其他并行系统类似,ECC也能以不同的算法级别来适用于不同的并行架构体系。文献[5-17]采用FPGA或ASIC等硬件实现,不具有灵活扩展性,因此不适用于大规模的并行系统。
现有的并行标量乘方法都是基于点或域操作级别的并行化,只适用于固定数量处理器(通常为2,3或4个处理器)的并行系统。本文的标量乘算法级别的并行化方法适应具有灵活数量处理器的并行计算系统,且具有很好的灵活性。各种标量乘并行方法比较如表1所示。
表1 各种标量乘并行方法比较

并行的标量乘方法并行处理器数量灵活性雅可比坐标并行表达式[5⁃6]2,3否双处理器架构表达式[7⁃8]2否替换乘方法[9⁃12]2,3,4否基于点操作的算术级别的并行化方法[13⁃17]2否本文提出的并行化方法2n是
本文的方法是基于最高的操作级别,现有的标量乘并行化方法也能集成到本文的方法中来进一步加快运算速度。而现有的标量乘并行化技术大多是基于椭圆曲线点或域操作的并行化。从某种意义上说,本文的方法对现有的并行标量乘方法是兼容的。因此,本文的并行标量乘方法的性能总能优于现有的并行标量乘方法。
7 结束语
串行的标量乘方法在并行系统中效率低下,并且现有的并行标量乘方法又局限于固定数量处理器的并行系统。本文提出的快速灵活的椭圆曲线标量乘并行化方法能适应各种规模的并行系统。既然本文提出的标量乘并行化技术是基于标量乘的算法级别,而不局限于椭圆曲线群结构,因此提出的划分与整合模型同样能适用于RSA加密系统的模幂运算的并行化处理。
[1] Miller V S. Use of elliptic curves in cryptography[C]// LNCS Advances in Cryptology. 1985,218:417-426.
[2] Koblitz N. Elliptic curve cryptosystems[J]. Mathematics of Computation, 1987,48(177):203-209.
[3] Knuth D E. The Art of Computer Programming Volume 2: Seminumerical Algorithms[M]. 3rd ed. Beijing: Tsinghua University Press, 2002:461-465.
[4] Hankerson D, Menezes A, Vanstone S. Guide to Elliptic Curve Cryptography[M]. Springer-Verlag, London, 2004:95-123.
[5] Aoki K, Hoshino F, Kobayashi T, et al. Elliptic curve arithmetic using SIMD[C]// Proceedings of International Conference on Information Security. 2001:235-247.
[6] Izu T, Takagi T. Fast elliptic curve multiplications with SIMD operations[C]// Proceedings of International Conference on Information Security. 2002:217-230.
[7] Izu T, Takagi T. A fast parallel elliptic curve multiplication resistant against side channel attacks[C]// Proceedings of the 5th International Workshop on Practice and Theory in Public Key Cryptosystems. 2002:280-296.
[8] Izu T. Fast elliptic curve multiplication resistant against side channel attacks[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2005,88(1):161-171.
[9] Mishra P K. Pipelined computation of scalar multiplication in elliptic curve cryptosystems[C]// Proceedings of the 6th International Workshop on Cryptographic Hardware and Embedded Systems. 2004:328-342.
[10] Longa P, Miri A. Fast and flexible elliptic curve point arithmetic over prime fields[J]. IEEE Transactions on Computers, 2008,57(3):289-302.
[11] Al-Otaibi A, Al-Somani T F, Beckett P. Efficient elliptic curve parallel scalar multiplication methods[C]// 2013 8th International Conference on Computer Engineering & Systems(ICCES). 2013:116-123.
[12] Azarderakhsh R, Reyhani-Masoleh A. Parallel and high-speed computations of elliptic curve cryptography using hybrid-double multipliers[J]. IEEE Transactions on Parallel and Distributed Systems, 2015,26(6):1668-1677.
[13] Bos J W. Low-latency elliptic curve scalar multiplication[J]. International Journal of Parallel Programming, 2012,40(5):532-550.
[14] Realpe-Munoz P C, Velasco-Medina J. High-performance elliptic curve cryptoprocessors over GF(2m) on Koblitz curves[J]. Analog Integrated Circuits and Signal Processing, 2015,85(1):129-138.
[15] Al-Somani T F. High-performance generic-point parallel scalar multiplication[J]. Arabian Journal for Science and Engineering, 2017,42(2):507-512.
[16] Asif S, Kong Yinan. Highly parallel modular multiplier for elliptic curve cryptography in residue number system[J]. Circuits, Systems, and Signal Processing, 2017,36(3):1027-1051.
[17] Oliveira T, Lopez J, Rodriguez-Henriquez F. The Montgomery ladder on binary elliptic curves[J]. Journal of Cryptographic Engineering, 2017,7(4):1-18.
