基于耦合策略的相依网络级联故障研究

徐红兵，张　维



基于耦合策略的相依网络级联故障研究

徐红兵1，张维2

(1. 万博科技职业学院，安徽，合肥 230031；2. 中国矿业大学，江苏, 徐州 221116)

随着基础设施网络的不断扩大，使得网络之间的相依性不断增加，导致相依网络系统中发生的级联故障较为严重。对此，本文提出了一个在相依网络系统中研究级联故障的理论框架，其中考虑了层内和层间的级联故障的影响，探究了跨层网络元件之间的不同耦合方式，即相依方式对级联故障的动态影响。通过利用提出的理论框架，对三种有代表性的耦合方式，即随机耦合、“低到高”耦合和“高到高”耦合，进行实验比较。结果显示，“高到高”耦合曲线非常接近Sfin=Sinit曲线，其余两个耦合方式在某些情况下导致电网最终级联故障增加了150%，在通信网中更严重；且在相依网络为一对一耦合模型下，两个相依网络节点的耦合方式对级联故障的最终影响程度起着关键作用，与其他形式的相依耦合方式相比，将两个网络的对等节点耦合，即“高到高”耦合所产生的级联故障较小，有效减轻相依网络级联故障的潜在策略。

相依网络；级联故障；耦合方式；跨层网络元件；“高到高”耦合；网元

0 引言

随着社会的迅猛发展，事物之间的连通性越来越强，这很大程度上取决于许多相依的物理基础设施网络系统，这些系统包括智能电网、智能交通、通信网络和全球互联网。典型的相依网络系统基础设施是电网和通信网络之间的关系，其中电网依靠通信网络将电力系统的状态信息传递到控制系统，并将中继控制信息传回电力系统，而通信网络依赖于电网的电源供给。由于这种相依性，一个网络中的元件故障，例如其用于传递智能电网控制信息的通信网络中的几个交换机发生故障，可能会导致电网的故障，而电网节点故障又导致通信网络中其他节点的故障，从而在这两个相依网络中产生级联故障。

级联故障对相依网络的影响日益增加，使得其成为研究人员的讨论热点，在单个网络的鲁棒性情况下，基于随机图模型或渗透理论的相依网络提供了对随机网络集合之间相依关系的一般统计特性的方法，然而，真实网络是确定、有限的。如电力网络和通信网络设计目的是为完成某些特定功能，其中许多功能可能不遵循“幂律”分布[1]。此外，尽管相依程度在控制相依网络的级联故障十分重要，但自治节点的数量不能完全确定，在某些情况中自治节点的数量是给定的。在这些情况下，设计不同层的非自治节点耦合方式是控制和减轻级联故障的另一有效的解决方案。Rosato等人[2]对电网和通信网络之间的相依关系进行了研究，结果表明即使在适度互联情况下，电网中的线路故障也可能会严重影响其通信网络。Ranjan提出了一种基于图形理论的有限网络模型[3]来表示相依网络，并引申了拓扑结构中心度测度[4]，从而衡量相依网络的鲁棒性。利用此鲁棒性测度方法，证明了两个相依网络的耦合节点的数量以及耦合方式在确定相依网络总体鲁棒性方面起关键作用。Nguyen等人对相依电网破坏因素（IPND）优化问题进行了研究[5]，以确定相依的电力网络移除某些节点会导致最大破坏结果的关键节点。

本文在已有的研究基础上，除考虑了不同层内和层间级联故障的影响之外，还研究了相依（“耦合”）方式如何影响相依网络中的级联故障，首先，提出了一种研究级联故障的理论框架级联故障模型，利用此模型，结合实际网络及合成网络评估结果，对三种有代表性的耦合方式，即“随机”耦合、“低到高”耦合和“高到高”耦合，进行实验比较，结果显示，“高到高”耦合方式产生的级联故障较小。

1 模型的提出

在相依的多层网络系统中的单个组成网络（也简称为多层系统的一层）中的网元的故障可能不仅触发本层内的级联，而且会触发多层网络系统的其他组成网络（层）中网元的故障。多层系统的层与层之间的相依性使得其级联故障可能与仅在一层内发生的级联故障在特征以及原因上非常不同，通常会对整个系统造成更广泛、更严重的损害。为评估、增强相依网络多层系统的弹性，必须了解相依关系如何影响多层系统层内和层间的级联故障的动力学特征[6]。

本文提出的相依多层网络系统中级联故障的理论框架模型，考虑不同层内和层间的级联故障的影响，目的是探究层间网络元件之间不同耦合（即相依关系）方式如何动态影响级联故障。为方便研究及实验验证，本文采用一个具有两个相同大小网络层的双层系统，并且在两层之间采用简单的一对一耦合映射。使用标准线性阈值模型对每层内的级联故障进行建模，研究在不同初始故障大小和级联阈值下，两个系统内不同“重要性”或“临界”（通过各种指标衡量，如节点度）节点的耦合情况如何影响各层内级联故障的动力学特性。在一对一耦合下，两个相依网络中的节点耦合方式，对最终级联故障的大小影响非常大：将来自两个网络的相应重要的节点，比其他耦合形式，如“随机”耦合或“高到低”耦合，产生的级联故障更小。特别地，双层系统的每层网络的拓扑相同时，“高到高”耦合方式会产生镜像效应，因为该耦合恰好反映每层内的级联情况，并且产生的故障不会比两个网络独立时的单层故障更大。

2　级联故障模型

考虑一个网络系统G（，），其中是节点集合，是边集合。一个节点子集产生级联故障并且导致一组较大数目的故障节点，级联故障建模过程如下：

其中P()是电网节点集合，Ƒ是该网络中的失效函数，其取决于节点（网络拓扑）的连通性以及故障是如何在网络中级联传播的。在大多数实际网络中，当节点与其他大部分节点不相连时，实际上节点在网络中几乎不起作用，即“失效”。线性阈值（Linear Threshold，LT）模型[7]很好地描述了这样的现象，即当其相邻节点（）中的失效比例已经大于某个阈值时，节点也被认为是失效的：

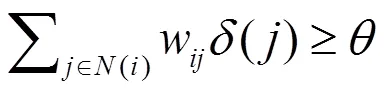
其中w是分配给相邻节点的权重，在归一化情况下，w=1。采用LT模型作为级联模型，即一个网络故障从一组节点发生故障开始，并且故障按照等式(2)在网络中进行级联传播。故障是逐渐严重的，即当节点出现故障时，整个过程不能恢复[8-9]。在逐渐严重级联模型中，给定和网络G可以确定。

但是，相依网络具有更复杂的结构，由多个网络（或层）组成，其中一个层中的节点需要来自其他层中节点的资源（例如电能），并且依次向其他层中的节点提供资源（例如控制信息）。在相依的网络中，一层中的节点故障导致其他层中的相依节点也将失败。例如，在图1中如果节点x2发生故障，则其他层中的相关节点，即y2和y3也会失败。因此，在相互依赖的网络中，一层中的初始故障不仅可能导致同一层内的级联故障，而且可能触发其他层节点级联故障。其他层次的级联故障又会触发原始层的进一步故障，从而产生可能导致整个系统故障的“恶性循环”。

T1∶V1→V2

为此，本文提出了一个理论框架来模拟和研究相依网络中的级联故障。与单层网络不同，在建立相互依赖的网络中，将不同层节点之间相依链路的功能与普通链路区别出来非常重要，因为单层故障和层间级联故障过程一般非常不同。例如，节点的故障通常不会自动导致同一层内的邻近节点的故障（除非LT模型下该节点的邻居节点的大部分失效）。另一方面，节点（即电源节点）的故障将导致其他层中的依赖节点（例如通信或控制节点）不发挥通信作用，因此高概率“失败”，除非提供某些保护机制（如备用电源）。即使在后一种情况下，这种保护机制通常具有时间性，如果故障节点没有及时恢复和恢复，只是简单地延迟了潜在故障。本文给出了具有两层G1（1，1）和G2（2，2）的相依网络的一般级联故障模型，其中Ƒ表示对层内级联故障进行建模的函数，T表示对层间级联故障进行建模的函数：

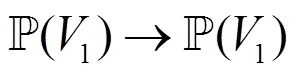
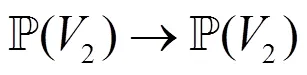
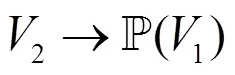
其中Ƒ1和Ƒ2不一定是单射或满射函数，由图1可知从层1到层2的双射函数T1。

3 仿真结果

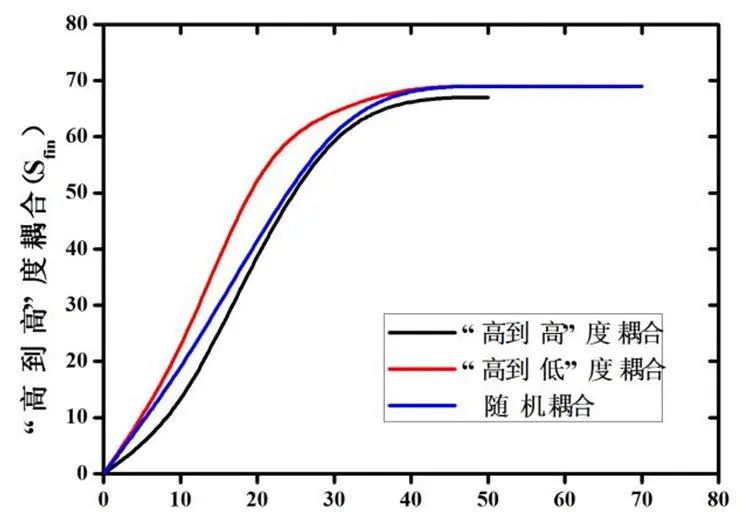
本文还在通信网中进行完全相同的一组模拟实验，令=68个节点。结果如图3所示。从图2和图3发现，“高到高”耦合比“低到高”和“随机”耦合产生的最终级联故障最小；而“高到高”曲线非常接近Sfin=Sinit曲线，另外两个耦合方式在某些情况下导致电网最终级联故障增加了150%，在通信网中更严重。其中，Sfin=Sinit曲线表示故障不级联传播并且最终故障大小等于初始故障大小的情况。

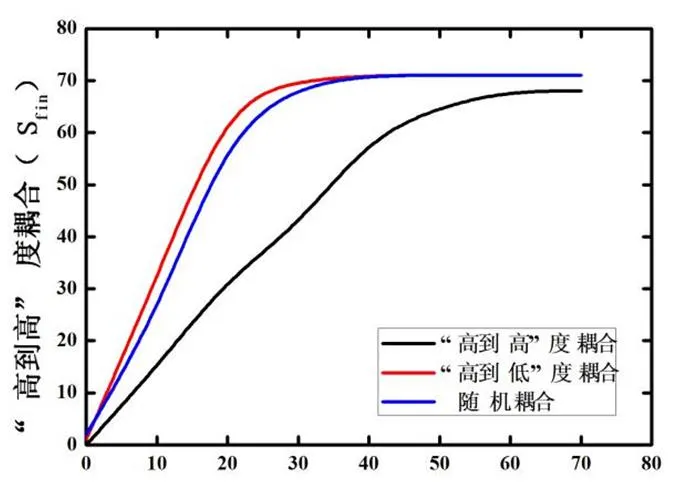
初始故障大小（Sinit）

图4显示了蓄意攻击下的故障结果：即更重要的中心节点作为攻击节点的结果。在本次实验中，具有较高等级的节点作为故障节点的初始集合。文献[10]与文献11]研究表明，实际网络的等级分布遵循幂律分布的比随机网络更容易受到蓄意攻击的侵害。实验结果表明，蓄意攻击情况下，相依网络中“高到高”耦合方式同样优于其他两个耦合方式，并对级联故障有更高的弹性。“随机”耦合失效结果是两层网络中随机耦合节点进行10000次实验的平均值。

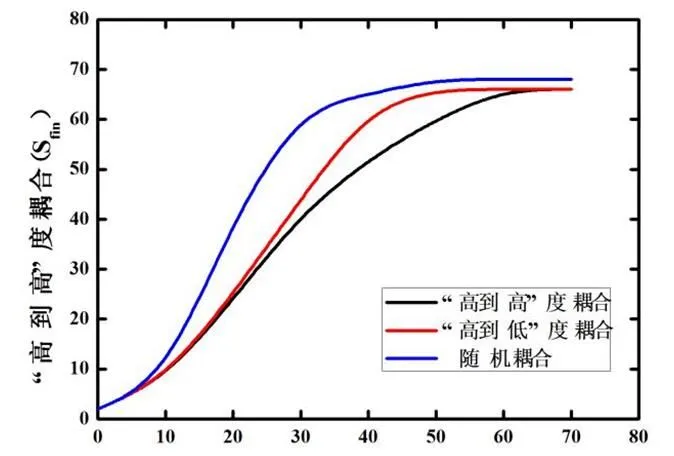
初始故障大小（Sinit）

若网络之间无相依关系，则在每个层中级联故障可能都是最小的。另一方面，相依网络中的故障可能导致“恶性循环”：当一层发生故障时，除了层内级联故障（式（3）中的Ƒ1）之外，还会触发层间故障（T1）。为了研究不同耦合方式对触发/减轻级联故障的影响，应将它们与单层网络中的级联故障进行比较。本文将三个耦合情况的级联故障与单层网络中的级联故障进行比较，如图5所示，该实验与图2中的实验相同，但是增加了最小可能的级联故障结果，即在电网单层网络中的级联故障结果。从实验结果可看出，“高到高”的耦合方式的最终故障大小实际上等于无相依关系的结果。这是由于镜像效应，该耦合关系精确地反映了两层中的级联情况，并且不会导致比单层级联故障更大的故障。因此，利用镜像效应，能够设计相依方式，以使相依网络中的级联故障最小化。在两层具有相同拓扑情况下，最佳耦合是对两层中的一致（等效）节点进行配对，即实验图5中“高到高”耦合方式。然而，当这些层不相同时，其找到最佳解决方案较为复杂，在这种情况下，应找到尽可能最好体现镜像效果的最有利的层次对齐方式。本文对两个具有不相似拓扑结构的相依网络进行了两次实验：=68个节点的相同大小的电网与通信网络（图6和图2）采用优先连接模型[12]进行耦合（图7）。实验结果显示，“高到高”耦合优于其他两个耦合，这表明“高到高”耦合（即实验中耦合层间的对等节点）在模仿镜像效应方面更为成功。

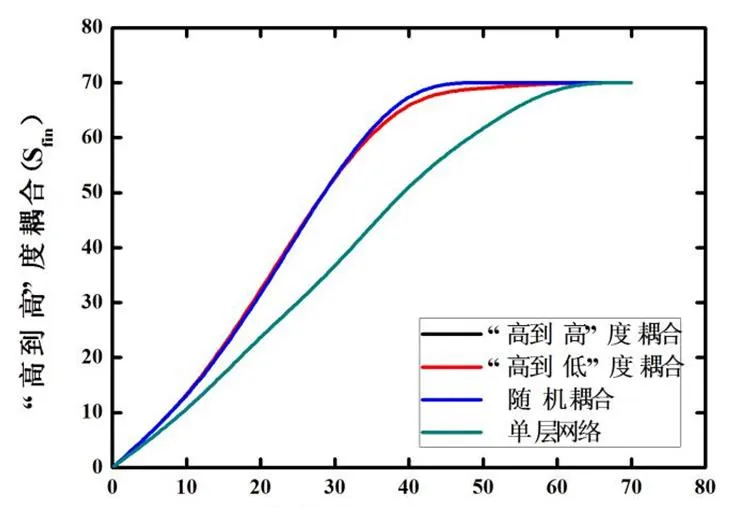
初始故障大小（Sinit）

初始故障大小（Sinit）

图7 电网与通信网的互耦网络中的两层优先连接模型

4 结论

为研究耦合策略对减小相依网络级联故障的影响，本文提出了一个研究相依多层系统中的级联故障的理论框架，考虑级联故障在不同层内和层间的影响，以探究跨层间网元之间的不同耦合（即相依关系）如何影响动态级联故障。通过使用提出的理论框架进行三种耦合方式的对比实验，结果显示，在一对一耦合下，相依网络的耦合方式在最终的级联故障严重程度中起关键作用，“高到高”耦合方式比“随机”或“高到低”耦合方式得到的级联故障较小。进而得出可以通过相依策略来减轻相依网络级联故障的程度。

未来将对“高到高”耦合方式的相依网络在不同攻击策略的鲁棒性进行研究，并引入对称级联方法来完善所提理论框架，以优化其性能。

[1] 龚贻华, 杜华, 李石兵,等. 超短波电台通信网络中的自组网路由协议应用研究[J]. 井冈山大学学报:自然科学版, 2017, 38(4):57-61.

[2] Rosato V, Issacharoff L, Tiriticco F, et al. Modelling interdependent infrastructures using interacting dynamical models[J]. International Journal of Critical Infrastructures, 2008, 4(1): 63-79.

[3] Ranjan G, Zhang Z L. How to “glue” a robust smart-grid: A finite network theory of inter-dependent network[C]. US: 7th Cyber Security & Information Intelligence Research Workshop, 2011: 12-16.

[4] 谈飞. 复杂网络上交通拥塞与级联故障的若干研究[D]. 杭州:浙江大学, 2014: 13-21..

[5] Nguyen D T, Shen Y, Thai M T. Detecting critical nodes in interdependent power networks for vulnerability assessment [J]. IEEE Transactions on Smart Grid (ToSG), 2013, 4(1): 151–159.

[6] Buldyrev S V, Parshani R, Paul G. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7): 1025-1028.

[7] Parshani R, Buldyrev S V, Havlin S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition [J]. Physical review letters, 2010, 105(4): 048701-048708.

[8] 王明. 考虑攻击风险的电力系统薄弱环节识别方法研究[D]. 重庆: 重庆大学, 2016: 26-34.

[9] Schneider C M, Yazdani N, Araujo N A. Towards designing robust coupled networks[J]. Scientific reports, 2013, 3(24): 1969-1974.

[10] 杨程成. 相互作用网络的鲁棒性研究[D]. 西安: 电子科技大学, 2015: 28-33.

[11] 刘军. 面向复杂网络的节点重要性排序和级联故障研究[D]. 重庆: 重庆大学, 2016: 31-38.

RESEARCH ON CASCADING FAILURES OF INTERDEPENDENT NETWORKS BASED ON COUPLING STRATEGY

XU Hong-bing1, ZHANG Wei2

(1. Wanbo Technical College, Hefei, Anhui 230031, China; 2. China University of Mining and Technology, Xuzhou, Jiangsu 221116, China)

With the expansion of infrastructure network, the dependence between networks is increasing, which leads to cascade failures in dependent network systems. A theoretical framework for studying cascading failures interdependent network systems was proposed, which considered the effect of cascade faults within and between layers, as well as explored the different coupling modes between network elements across layers, that is the influence of cascading failures on interdependent network. By using the proposed theoretical framework, three representative coupling modes, namely, random coupling, 'low to High' coupling and 'high to High' coupling, are compared experimental. The results show that the "high to high" coupling curve is very close to the Sfin=Sinitcurve, and the other two coupling modes lead to a 150% increasing in the final cascading failures in some cases which is more serious in the communication network. In addition, in the case of one-to-one coupling model of dependent network, the coupling mode of two dependent network nodes plays a key role in the final impact of cascaded faults. Compared with other forms of dependent coupling, the coupling of two network peers, that is "high to high" coupling mode produced little cascading failures, which can efficiency reduce the potential strategy of cascading failures in dependent networks.

interdependent networks; cascading failures; coupling modes; cross layer network components; high to high coupling; network elements

1674-8085(2018)05-0001-05

A

10.3969/j.issn.1674-8085.2018.05.011

2018-05-17；

2018-08-11

安徽省高等学校自然科学研究项目（KJ2018A0753）

*徐红兵(1974-)，男，安徽庐江人，讲师，主要从事计算机网络、人工智能等方面的研究(E-Mail: Xuhongb1974wb@sohu.com);

张维(1983-)，女，江苏徐州人，硕士，副教授，主要从事通信技术，无线传感器网络等方面的研究(E-Mail: ZhangW1983min@sohu.com).