重视试题的本质探究，发挥问题的教学价值——以2018年高考数学浙江卷第17题的探究为例

☉浙江省平湖中学 高玉良

☉浙江省嘉兴市第一中学 沈新权

2018年高考已经落下帷幕，各省市的高考试卷中都有不少体现新课改理念的试题，这些试题的求解都有角度宽、视点多、层次好的特点，能够很好地考查学生的数学基础、对数学本质的理解能力和数学的理性思维能力，注重对数学思想方法与数学核心素养的考查.如果我们对这些“雅俗共赏”的试题认真研究，仔细品味，那么这些试题不仅仅是我们“津津乐道”的好题，更是我们日常教学中“深入浅出”的教学素材.

下面以2018年高考数学浙江卷的第17题为例，来谈谈我们的解题感受和该试题对高中数学教学的一些启示.

一、试题呈现，立意分析

A，B满足A■→P=2P■→B，则当m=______时，点B横坐标的绝对值最大.

本题是试卷填空题的最后一题，属于压轴题.本题题干简洁，但问题的内涵丰富，设问方式不落俗套.问题中“明”的参数是m，但“暗”的参数则是隐藏在题目背后的直线AB的斜率.要计算点B横坐标的绝对值的最大值，我们可以m为变量，也可以直线AB的斜率为变量，甚至还可以求出点B的轨迹方程.

二、策略探寻，一题多解

方法1：以m为变量，通过向量的坐标关系，将点B的横坐标转化为关于m的目标函数进行求解.

图1

设A（x1，y1），B（x2，y2），P（0，1），则（-x1，1-y1），P■→B=（x2，y2-1）.

方法2：以直线AB的斜率k为变量，通过向量的坐标关系，将点B的横坐标转化为关于k的目标函数进行求解.

设A（x1，y1），B（x2，y2），则（-x1，1-y1），■=（x2，y2-

当直线AB的斜率不存在时，x2=0，此时m=9.

当直线AB的斜率存在时，设直线AB为y=kx+1，代入方程+y2=m（m＞1），可得（1+4k2）x2+8kx+4-4m=0.由m＞1知，点P在椭圆内部，故一定有两个交点，由韦达定理得当且仅当|k|=时取等号，此，解得m=5.

点评：此法学生入手容易，将直线与椭圆的位置关系转化为方程组的解的问题，通过韦达定理和向量的坐标运算将点B的横坐标用直线AB的斜率k进行表征，转化为型函数的最值问题求解，可用基本不等式简化运算，事实上，由对称性不妨设x1＜0，x2＞0，由可知k＞0，则，当且仅当时取等号，可得m=5.

方法3：运用椭圆的参数方程，把点B的坐标设成点参的形式，然后借助三角关系进行消参.

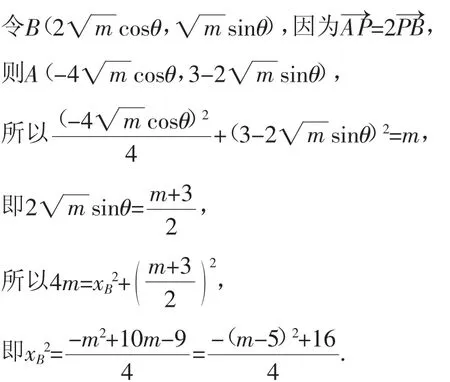
当m=5时，点B横坐标的绝对值最大.

点评：此法通过椭圆的参数方程将椭圆上点的横纵坐标x，y统一成θ的形式，将向量关系转化为A，B两点坐标关系，运用三角恒等式sin2θ+cos2θ=1简化计算，最终转化为二次函数f（x）=ax2+bx+c的最值问题求解，简单明了.

当m=5时，|x2|max=2.

点评：学生对圆锥曲线中的中点弦问题用点差法非常 熟 悉 ， 本 题 通 过知与普通的点差法相比需要配系数，有一定技巧性，此种解法胜在计算量小，也是转化为二次函数f（x）=ax2+bx+c的最值问题求解，直截了当，不绕圈子.

所以|xB|max=2，此时，可得m=5.

点评：直线的参数方程是高中数学选修内容，在高考中并未涉及，此法通过直线参数方程将目标函数转化为求型三角函数的最值问题求解，可联想到斜率的几何意义，也可求导求解，计算量较大，不适合解填空题.

策略3：解析几何终究还是几何，如果能从几何的视角分析问题、解决问题，则能收到事半功倍的效果，也利于分析题目的本质含义.

方法6：如果我们把椭圆化为圆，那么隐藏在问题中的几何性质就“昭然若揭”，而把椭圆化为圆，只要利用合适的换元即可.

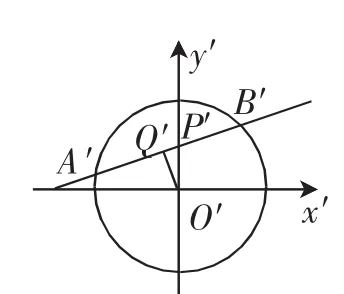
图2

通过仿射变换T将椭圆变成圆，利用直线与圆的位置关系及垂径定理等平面几何知识，将代数问题转化为几何问题，四两拨千斤，大大减少计算量.

策略4：既然点B是运动的，我们能不能求出其轨迹方程呢？由A■→P=2P■→B我们可以把点A的坐标用点B的坐标来表示，而且已知条件中的椭圆系是离心率不变的椭圆系，因此，利用椭圆的垂径定理可以求得点B的轨迹方程，然后求出其横坐标的最大值.

图3

方法7：如图3，设B（x0，y0），由=2得A（-2x0，3-2y0），从而AB的中点坐标为，由椭圆垂径定理得，化简得，即|x0|max=2，此时y0=2，代入=m（m＞1）得到m=5.

三、解后反思，感悟教学

（1）这是一道不可多得的高考试题.虽然它考查的内容依然是圆锥曲线中的热点问题——范围问题，但其形式简洁，解题入口较宽，思维方法多样，各种方法之间又有密切的联系，既突出考查了学生的数学运算能力，又不露痕迹地考查了学生的逻辑推理、数学抽象、直观想象等数学核心素养，这恰恰体现了解决高考数学试题所需要的思维特点：“想得少一点，算得多一点；想得多一点，算得少一点”，以此区分学生的思维层次.因此，这又是一道有“思想”的数学试题.

（2）数学家波利亚曾说过：“没有任何问题是可以解决的十全十美的，总剩下些工作要做.经过充分的探讨与钻研，我们能够改进这个解答，而且在任何情况下，我们总能提高自己对这个解答的理解水平.”所以，要提高高考数学的复习效率，教师要首先重视解题研究，正如数学家弗里德曼在《怎样学会解数学题》一书中所呼吁的那样：“应当学会这样一种对待习题的态度，即把习题看做是精密研究的对象，而把解答习题看做是设计和发明的目标.”通过教师的演示，引导学生学习数学不仅仅是解题，而解题也不单单是为了找到答案，从而逐步培养学生自主探究数学的能力.

（3）陕西师范大学的罗增儒老师指出：“我们的解题实践表明：分析典型例题的解题过程是学会解题的有效途径，至少在没有找到更好的途径之前，这是一个无以替代的好主意.”什么样的问题是典型的问题？除了高中数学中一些经典的问题，每年高考试卷中所涌现出来的高考试题无疑是值得我们研究的对象.高考数学试题里面蕴含着巨大的思想财富，教师在教研过程中要善于挖掘高考数学试题所特有的教学功能，不仅要重视对典型高考试题的一题多解的研究，更要引导学生在问题探究的过程中透过纷繁复杂的外表看清问题的本质，加强对数学知识背景及数学本源的挖掘，在知识的纵横联系中让学生真切地感受到知识的来龙去脉，感悟到解题方法的自然和谐，借此培养学生数学思维的深度、厚度和广度，真正提升学生的数学核心素养.H