立足根本，枝繁叶茂——一道“解三角形试题”的解法探究

☉浙江省诸暨学勉中学 潘 波

近年浙江高考数学的“解三角形”问题逐渐成型，考查学生的方向也尤为明朗，如考查内容离不开“两个定理，三个公式”，但题型的呈现变化莫测，为寻找一条有效的解题途径，让学生面对此类问题能有的放矢，化解自如，我们从一道“解三角形试题”的解法开始谈起.

一、众里寻它千百度——选题

“一题可破万题山”.选择一道合适的“题”，能够帮助学生明晰概念，掌握方法，所以，抓住一道好题，让学生寻求多种解题途径，促使学生的思维向多方位发散，这比题海战术更为有效.

例题 已知△ABC内角A，B，C所对的边分别为a，b，c，且ccosA-acosC=2b.

（2）若c=3，求△ABC面积的最大值.

评点：例题的已知条件“ccosA-acosC=2b”为边角的关系，可以从多角度思考展开，如边化角，角化边，因其形式上类似射影定理“ccosA+acosC=b”，所以还可以结合射影定理展开思路，从构造直角三角形入手，它很好地运用正弦、余弦定理解题，从课本定理本源出发，从引申的结论出发，无不是一个好背景.一题多解，发散学生的思维，促进学生数学思维的活跃性.选择本题，能够达到“解一题等于解一类‘三角’问题”的效果.

二、不畏浮云遮望眼——解题

“授人以鱼不如授人以渔”.数学家苏步青教授曾说：“学习数学要多做题，边做边思索，先知其然，然后知其所以然.”通过解一道题，加以思索，总结方法，“知其所以然”，不管题型如何变化，总可以寻找到一个或多个思考的方向.

解法1（边化角）：（1）由正弦定理及已知条件可知，

sinCcosA-sinAcosC=2sinB=2sin（A+C）=2（sinAcosC+sinCcosA），则sinCcosA=-3sinAcosC，

△ABC

图1

评点：已知边角的关系，因为所求的目标为角，一般将等式中的边利用正弦定理化为角，便于运算；对（2）中的边化角角度求面积问题，运算简洁，易懂，其根本还在于构造直角三角形，这与课本中提供的构造直角三角形证明正弦、余弦定理相符.

（2）由（1）得c2=a2+2b2，则2abcosC=a2+b2-c2=-b2，

评点：已知边角的关系，一般说来，边化角法可解，角化边法亦可解，原因是正弦定理、余弦定理是可以互证的，只是有时不同方法选择有易有难，所以更多时候要求选择更简洁方便的方法解题，而求三角形面积问题，要从三角形面积的一些相关公式入手，如海伦公式等，同时其根本还是将面积中的边角统一转化.

解法3（射影定理）：（1）如图1，过B作BD⊥AC于D，由射影定理ccosA+acosC=b.又已知ccosA-acosC=2b，则ccosA=，所以ccosA=-3acosC，于是sinC·cosA=-3sinA·cosC.

评点：正弦定理、余弦定理的推论，得射影定理ccosA+acosC=b，此为课本课后的习题，可以结合几何意义来运用，其根本还在于构造直角三角形，将一般三角形特殊化，简化问题.

解法4（构造直角）：（1）由题意得，角C为钝角，如图2，过B作BD⊥AC，交AC的延长线于D，则|AD|+|CD|=2b.又由图2易知，|AD|-|CD|=b，于是

（2）如图2，分别过点C，D作AB的垂线，垂足分别为E，F，

图2

在Rt△ABD中，由射影定理得|DF|2=|AF|·|BF|.

另解：由上述可知S△ABC=|DF|，易知点D在以AB为直径的圆上，如图3，于是，所以

图3

评点：因正弦定理、余弦定理的“根本”在于构造直角，特别是（2）中的另解，结合圆处理方便简洁，这也是在圆上证明正弦定理所派生出来的解题思路.

解法5（向量转化）：（1）如图4，以A为原点，建立直角坐标系，则A（0，0），B（3，0），设D（x，y）.

图4

所以x·（x-3）+y2=0，即x2+y2=3x.

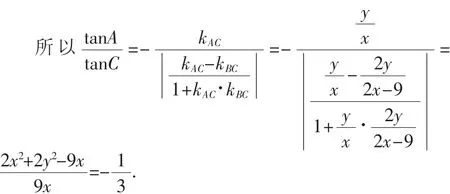
（2）由（1）得到x·（x-3）+y2=0，则y= ■ x · （x-3），其中0＜x＜3，则y≤.

解法6（向量转化）：（1）由已知ccosA-acosC=2b，

则bccosA-bacosC=2b2，

因为c2-a2=2b2，c=3，

评点：正弦定理、余弦定理的证明可以用向量法轻松证明，所以很好地给了我们向量方法的解题思路，而且也非常简洁，特别是（2）对面积的转化，将面积转化为S△ABC=y，后面的问题也就迎刃而解了，很成功，很有效.

三、接天莲叶无穷碧——变式

高考试题的特点为“源于教材，但又略高于教材”.所以我们不能孤立于课本的教学，甚至不能运用题海战术盲目地做题，而要学会对课本上的例题、习题做适当的改编.编题可以运用多种方法，如推广引申法、逆向思维法、极端原理法、知识重组法等，让学生在开放的题海中感受解题.

变式1：已知△ABC的内角A，B，C所对的边分别为a，b，c，且ccosA=-3acosC，tanA=，求tanB的值.

变式2：已知△ABC的内角A，B，C所对的边分别为a，b，c，且acosC-ccosA=b，求tan（A-C）的最大值.

变式3：已知△ABC的内角A，B，C所对的边分别为a，b，c，且ccosA=2b，求的值.

变式5：已知△ABC的内角A，B，C所对的边分别为a，b，c，且2acosB=b+c，求的取值范围.

变式6：已知△ABC的内角A，B，C所对的边分别为a，b，c，且ccosA-acosC=2b，若△ABC面积的最大值为求c的值.

变式7：已知△ABC的内角A，B，C所对的边分别为a，b，c，且ccosA-acosC=2b，若△ABC面积为，求c的最小值.

评点：变式1中等价改变条件，而实际上“ccosA=-3acosC”等价于“ccosA-acosC=2b”，由上述解答可知已知tanA必可求tanC，于是tanB的值也就可以确定了；变式2中，不给tanA的值，但tan（A-C）会存在最大值；变式3，4，5都是改变已知条件，特别是变式4的已知条件确定角B此时的存在范围，变式5的已知条件用了2016年的考题条件，可确定A，B两角的关系，方可求的取值范围；变式6和7调换未知与已知，变式6若给出三角形面积的最大值，则也就确定了边c，倘若只是确定三角形的面积，此时会存在边c的最小值.这些变化的解法还是离不开以上给出的方法，同时也很好地呈现了本块知识的考点，所以题目不管如何变化，方法得当，迎刃而解！

“映日荷花别样红”.数学是思维的体操，启迪思维是数学教学的核心，是否有利于启迪思维可以作为判断一道数学题好坏的依据.上述题很好地综合了解三角形章节的所有知识和方法，思维和能力，同时能紧扣数学概念本质，立足知识的“根本”将原题进行变式，多角度，全方位挖掘概念内涵，必能达到“枝繁叶茂”的效果.W