基于模糊综合评判法的高职院校教师教学质量评价

2018-12-12马桂州

潍坊工程职业学院学报 2018年6期

马桂州

(汕尾职业技术学院，广东汕尾 516600)

一、高职院校教师教学质量学生评价指标体系

建立教学质量评价指标体系是开展教学质量评价工作的前提。高职院校教师教学质量评价体系，涉及到很多因素，在多种因素的综合考虑下，根据方向正确、指标科学、层次分明、具有可操作性等构建原则，建立如表1所示的高职院校教师教学质量学生评价指标体系[1]。

二、模糊综合评判法基本原理

模糊综合评判法是一种建立在模糊数学基础上的评价方法。这种方法利用模糊数学理论把定性评价转化为定量评价，对受到很多条件影响的对象做出一个综合评价。模糊综合评判法中的主要步骤包括[2]：

1.确定因素集F和评定集E

因素集F即评价项目或者指标的集合，一般有F={f1},i=1,2,…,n。评定集E即评价等级的集合，一般有E={ej},j=1,2, …,m。

2.确定隶属度向量，并形成隶属度矩阵R

所谓隶属度rij，是指多个评价主体对某个评价对象在fi方面作出ej评定的可能性大小。

隶属度矩阵R=(R1，R2，…,Rn)T=(rij)。

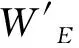
4.按照某种运算法则，计算综合评定向量S和综合评定值μ

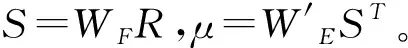
三、模糊综合评判法在学生评价模型中的应用

选取某个有50名学生的班级对某科任教师进行评教打分，然后参照表1，对学生评价该教师的教学质量的结果进行模糊综合评判。考虑到评价指标不止一层，因此采用多层模糊综合评判法。

表1 高职院校教师教学质量评价指标

(一)确定因素集和评定集

因素集即评价项目或者指标的集合，确定学生评价包括二级指标和一级指标2个层面的因素集。二级指标因素集分别为F1={E11，E12，E13,E14,E15,E16},F2={E21，E22，E23,E24,E25},F3={E31，E32，E33,E34,E35},F4={E41，E42，E43,E44},一级指标因素集F={E1，E2，E3，E4}。

评定集即评价等级的集合，确定学生评价的评定集为E={优秀，良好，中等，及格，差}。

(二)确定底层隶属度矩阵和底层权重向量矩阵

50位学生打分的结果统计如表2。学生对该教师的教学态度E1、教学内容E2、教学方法E3、教学效果E4的隶属度矩阵分别为：

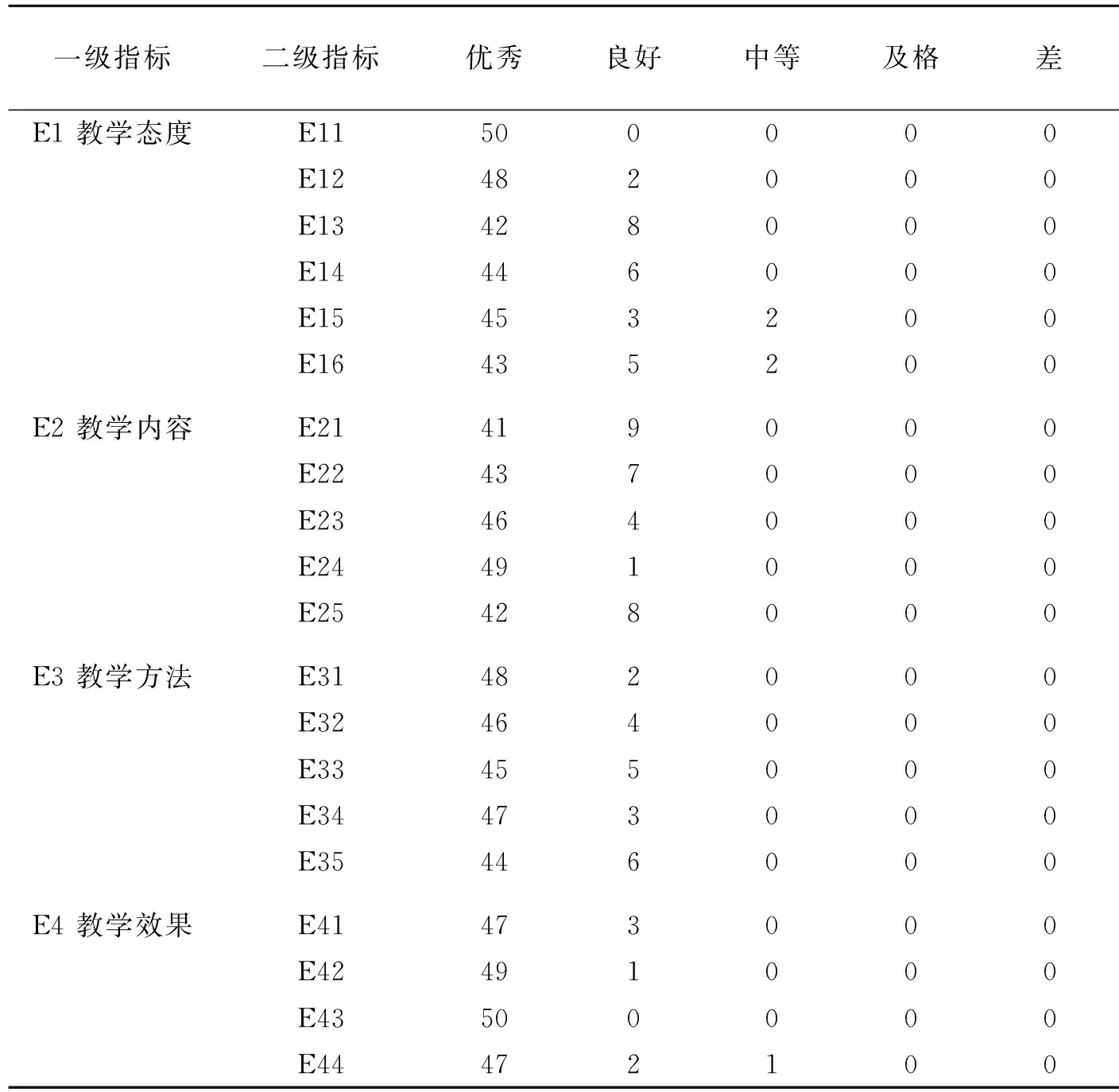
表2 学生评教打分结果统计表

根据学生评教打分结果统计表进行换算，可以得到学生评教隶属度统计表如下：

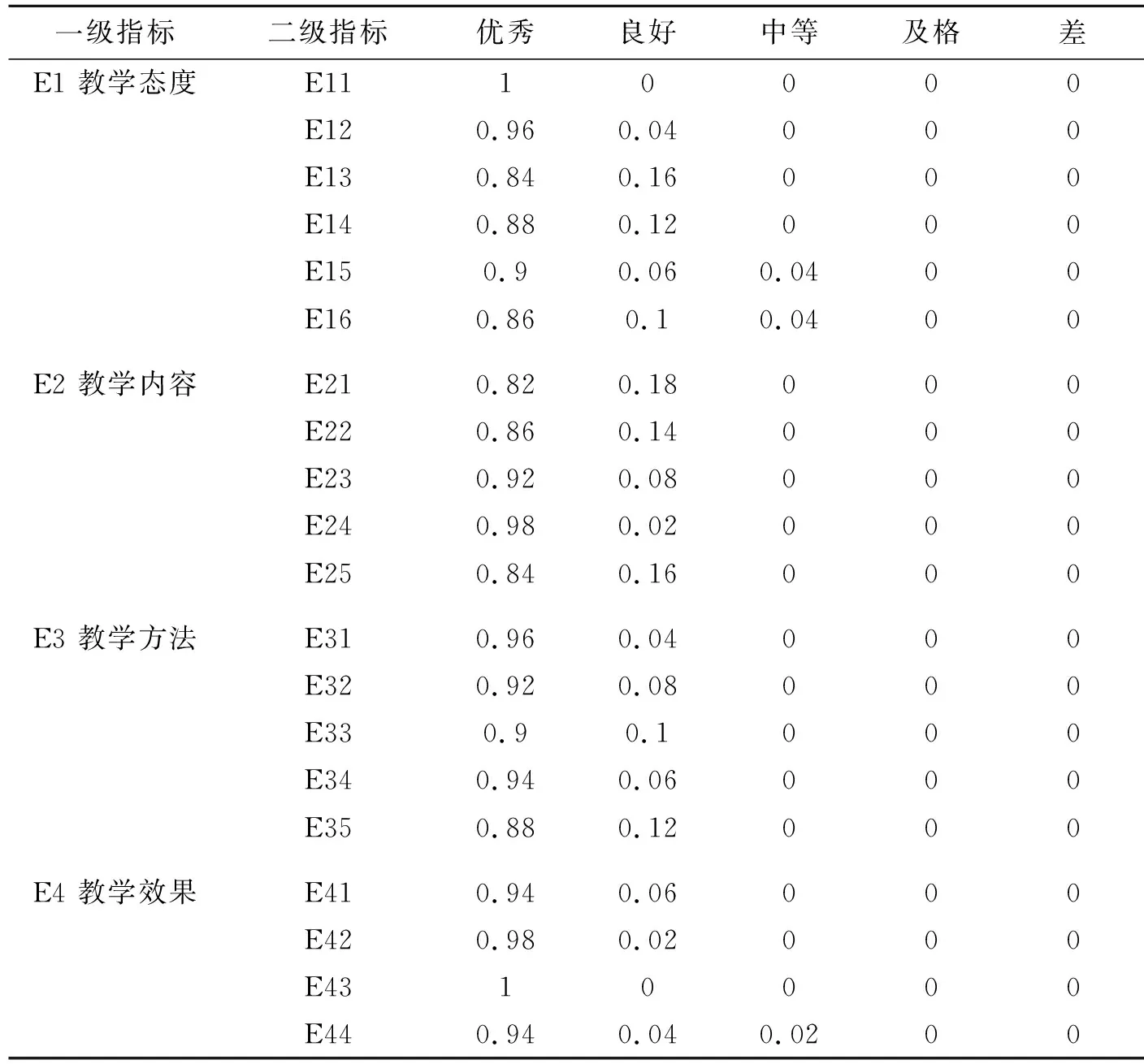
表3 学生评教隶属度统计表

根据表1的二级指标权重，可得到教师的教学态度E1、教学内容E2、教学方法E3、教学效果E4的权重向量矩阵分别为：

Wl=(0.131，0.161，0.186，0.114，0.251，0.157)

W2= (0.285，0.152，0.236，0.113，0.214)

W3=(0.155，0.134，0.217，0.253，0.241)

W4=(0.316，0.211，0.277，0.196)

(三)计算综合评定向量

学生对该教师在教学态度E1、教学内容E2、教学方法E3、教学效果E4上的评判结果体现为下面4个综合评定向量S1、S2、S3、S4：

=(0.90304，0.08064，0.01632，0，0)

=(0.87204，0.12796，0，0，0)

=(0.91728，0.08272，0，0，0)

=(0.96506，0.03102，0.00392，0，0)

将S1、S2、S3、S4这4个综合评定向量进行组合，得到该班学生对该教师教学质量评价的隶属度矩阵为：

根据表1的一级指标权重，可得到教师的教学质量评价的权重向量矩阵为：

W=(0.145，0.342，0.297，0.216)

这50位学生对该教师的教学质量的评判结果体现为学生评教综合评定向量S：

=(0.9100636，0.08672328，0.00321312，0，0)

从上面的学生评教综合评定向量S中得到：“优秀”档次的隶属度为0.9100636，“良好”档次的隶属度为0.08672328，“中等” 档次的隶属度为0.00321312，“及格”档次以及“差”档次的隶属度均为0。

(四)计算教师教学质量学生评价得分

考虑到很多高职院校需要对教师教学质量的评价结果进行排名，以体现教师之间的差别。因此，需要对综合评价的结果进行量化处理。定义“优秀”档次的分值区间为“大于或等于90分，小于或等于100分”；“良好”档次的分值区间为“大于或等于80分，小于90分”；“中等” 档次的分值区间为“大于或等于70分，小于80分”；“及格” 档次的分值区间为“大于或等于60分，小于70分”；“差” 档次的分值区间为“大于或等于0分，小于60分”。