数学解题目标意识培养的重要途径

甘肃 袁 琳

波利亚说：“学习数学就意味着学会解题”，如何将解题做到科学、规范、严谨，达到融会贯通、心领神会，是每个数学学习者的目标.

然而，笔者所属贫困地区的数学教学不仅因有限的教学资源而制约，而且因学生的数学素养低、思维灵活性差而低效.从学生的解题实践活动中，不难发现解题往往缺乏导向性、完备性、系统性.常会出现以下几种解题偏轨现象：

1.注重了试题条件的任性分析，忽视了试题结论的目标导向.

2.注重了试题结论的目标探索，忽视了试题条件的受限剖析.

3.虽然既注重了试题的条件，又注重了试题的结论，但是在条件与结论间难以建构解题的通道口，在条件与条件间找不到连接点.

解题偏轨的根本原因在于学生解题的目标意识不强，目标思维欠缺，目标分解断层.为了培养学生的解题目标意识，提高数学解题能力，在课堂的解题教学中，需加强解题的以下思维培养：

1.研判目标的原本性.要理解目标结论的内涵是什么？外延是什么？通过观察、类比、猜想、转化等思维过程，认清问题的结论所揭示的事实，理清问题的结论结构.

2.强化目标的导向性.要解(证)某一结论，需解(证)哪些中间结论，要解(证)中间结论，还需解(证)哪些结论，逐层推进，直至与已知对接.

3.提升解题的系统性.在一个纵横交织的知识网络、思维漩涡解题进程中，要整理出解答问题的层次结构，先后顺序，就需将目标结论与题设条件放在同一平台，剖析条件与结论间具有的内在因素，分析条件与条件间的串并关系，并有机地、有序地组合于一体，形成系统的解题思路.

如何将学生的解题目标意识培养落实到具体的教学中去，又有哪些有效的途径呢？笔者曾做过一些问卷调查、实践尝试及深度反思.现将个人的一些见解整理如下，以供同仁指正.

一、借助反置思维，探寻解题的目标入口

反置思维就是把试题中的结论反置为条件，以结论为解题的抓手，并与题设的部分(或整体)条件有机结合，通过转化、推演，得出一个题设条件的“结论”，或是不证自明的“结论”，这个“结论”便是解题的目标入口.

在解题中，常遇到此情形：面对一个题设条件过于单一或过于复杂的问题，由于条件与待解(证)的结论之间的“代沟”过大，难以形成思维的共鸣，无法架构思维的桥梁，从而使得问题解答找不到思路的基点，怎么办呢？有一个行之有效的办法——反置思维，或许能拨云见日，化解解题的疑难.

反置思维视角下的解题分析：该题所给的仅仅是一个问题的情景，显性的约束条件少，思维的口子宽，从哪里下“刀”，切开这个“题糕”呢？这个第一“刀”是解题的难点，也是关键点.下面通过反置思维进行挖掘解决问题的目标入口.

二、渗透数学思想方法，打开解题目标的通道

数学思想是数学的灵魂，数学方法是数学的躯体，数学思想与方法是解题的指导法宝.合理、准确地运用数学思想与方法来解题，有利于确立解题的方向，有利于高视角下分解与组合问题的主干结构，有利于优化思维结构，为解题的目标意识注入新的活力.

案例二：已知不等式ax2-2x+b>0的解集为(3,5)，则实数a,b的值分别为________.

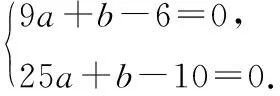
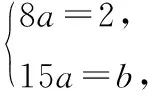
三、引入思维导图，构建解题目标的系统

数学解题的思维导图就是运用图文并重的方法，把试题的各级知识点的关系，用相互隶属与相关的层级图表现出来，形成一个解题的思维的形象的系统.

初对一个题设条件相对多，结论相对抽象的问题，或许我们的解题是迷茫的，不知所措，是从哪个条件着手呢？要解(证)目标结论，得需解(证)哪些中间小目标结论呢？不妨引入数学思维导图，从导图中寻求解题的思维方向，建构解题的层级目标，形成解题的目标系统.绘制数学思维导图，有利于培养学生的分析问题的能力，整合知识的能力，有利于提高学生思维的系统性、完备性，为数学解题的目标意识的培养奠定一个坚实的技术指导.

那么，如何绘制思维导图呢？首先，将结论作为解题的根圈，然后剖析给定的每个条件，提示其具有的数学本质，并作为解题的叶圈.接着，内化条件，相互转化，推出所需小目标结论，以连线方式结成枝干.最后，理清各个枝干的内外层级、因果关系、前后顺序，有机地镶嵌到根圈上，形成一个完整、完美、和谐的解题路线图.

案例三：设函数f′(x)是奇函数f(x)(x∈R)的导函数，f(-1)=0，当x>0时，xf′(x)-f(x)<0，求使得f(x)>0成立的x的取值范围.

思维导图视角下的解题分析：在绘制思维导图时，首先要明确以下几个解题的重要小目标：

1.待解结论是抽象函数不等式的解集，这类问题的一般性解题的策略是什么？

此类问题的一般性解题策略为：利用函数的单调性脱去函数的符号“f”，化抽象不等式为具体不等式，并运用不等式的性质加以解答.显然，一般性解题的策略给出了解题的总目标是做什么的，为解题指明了方向.

2.由条件“x>0,xf′(x)-f(x)<0”你能联想到什么？它所揭示的问题的本质是什么？在实现总目标的过程中，能起到什么作用呢？

3.条件“函数f(x)(x∈R)是奇函数”从“形”的角度而言，函数的奇偶性刻画了函数的什么特性？在实现总目标的过程中，又能起到什么作用呢？

函数的奇偶性刻画了函数图象的对称美，偶函数的图象关于y轴对称，奇函数的图象关于原点对称.由2中的条件仅能研究(0,+∞)的函数图象的变化趋势，而(-∞,0)的函数图象的变化趋势，就根据奇函数的对称性而得之.

4.条件“f(-1)=0”是用来干什么的？在实现总目标的过程中，又有什么作用呢？

在解题过程中，条件f(-1)=0的作用有二：其一，与条件“函数f(x)(x∈R)是奇函数”对接，可得f(1)=0；其二，由1可知：抽象函数不等式的解题的一般策略是利用函数的单调性脱去函数符号，在脱这个符号“f”时，需将待解目标 “f(x)>0”化为“f(x)>f(x0)”的形式，也就是说，条件“f(-1)=0”是用来替代f(x)>0中的0的.

5.不等式g(x)>0与f(x)>0的解集有何关系？

根据以上的解题的分析与思考，可绘制如下的思维导图：

(本文是甘肃省教育科学“十三五”规划“陇原名师”专项课题“数学解题目标意识培养”(课题立项号：GS[2017]MSZX034)研究成果)