轨迹思想在解三角形中的应用

安徽 胡 广

解三角形是高中数学的重要内容，也是高考的重点考查对象.解三角形的主要方法是根据正余弦定理以及三角形中的边角关系，然后利用相关三角函数公式等数学知识进行三角形中边角及面积等元素的计算.有些三角形问题还能与函数、不等式等知识结合，另外有些三角形问题如果能从轨迹思想入手，还可以将三角形问题转化为解析几何的问题.下文结合具体例题谈谈笔者的一些体会.

一、与圆结合

类型1：与三角形的外接圆结合

求 (1)△ABC面积的最大值；(2)a2+b2的最大值.

常规解法:(1)在△ABC中，由余弦定理，得c2=a2+b2-2abcosC. 即3=a2+b2-ab≥2ab-ab，得ab≤3.

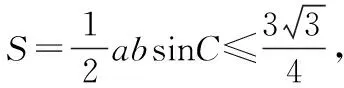
用轨迹方法求解：

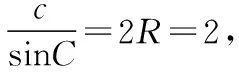
(2)设C(x,y)，则

比较两种解法可以发现，用轨迹思想处理相关的最值问题时，C点的位置对最值的影响比较直观，所以解决起来比较方便.

类型2:与阿氏圆结合

(在平面上到两定点距离之比为定值(定值不为1)的点的轨迹是圆)

示例2：在△ABC中，BD是∠B的平分线，且AD=1,CD=2，求△ABC面积的最大值.

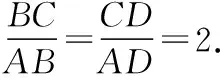
用轨迹方法求解：不妨设D为坐标原点，AC边所在直线为x轴建立直角坐标系如下图.则A(-1,0),C(2,0)

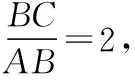
易知当B点位于(-2,±2)时，△ABC面积最大，此时S=3.

相对于常规解法而言，本题利用轨迹思想大大简化了解题步骤，建立了三角问题与解析几何之间的联系.

类型3：与其他圆的结合

示例3：在△ABC中，AB=2,AC2+BC2=8，求△ABC面积的最大值.

用轨迹方法求解：不妨以AB中点为原点，AB所在直线为x轴建立平面直角坐标系如下图，则A(-1,0),B(1,0),令C(x,y),

除了上述情形外，有些三角形问题还可以与圆锥曲线产生联系.

二、与圆锥曲线结合

类型1：与椭圆结合

示例4:在△ABC中，角A,B,C对应的三边分别是a,b,c.已知b=2,a+c=4,求中线BD的范围.

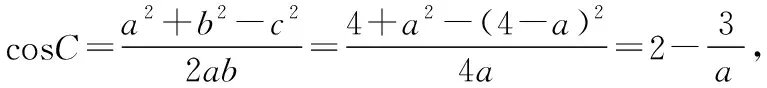
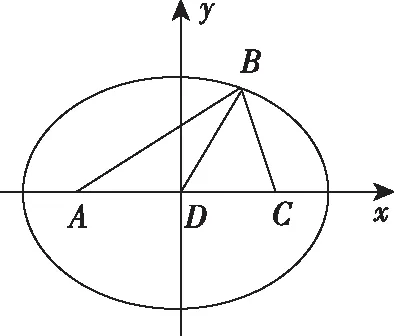
用轨迹方法求解：以D为坐标原点，AC边所在直线为x轴建立直角坐标系如下图，∵AB+BC=4,∴B点的轨迹是以A,C为焦点的椭圆(不包括长轴的两个端点),

类型2：与双曲线结合

示例5：在△ABC中，角A,B,C对应的三边分别是a,b,c.已知BC=10,AB-AC=8.求sinB的取值范围.