双弹簧问题归类剖析
2018-12-06江西
江西 陈 明
弹簧在生活中很常见,而弹簧模型是高中物理中一个重要模型,可与物理中的诸多知识点有机结合来考查同学们的分析能力和推理能力。本文将对一个题中出现两个弹簧的问题进行分析探究,本文中的弹簧模型都是轻质弹簧模型。
一、弹簧弹力
弹簧可以被拉伸也可以被压缩,因此弹簧的弹力具有双向性,弹簧弹力大小与弹簧的形变量遵循胡克定律,即F=kx,但只能判断出弹簧弹力的大小,不能判断出弹力的方向。
【例1】如图1所示,一重为12 N的物块上、下两端分别与两根完全相同的竖直轻弹簧a、b相连,弹簧a的上端固定在天花板上,弹簧b的下端固定在桌面上。当物块静止时,两弹簧的弹力大小相等,此时两弹簧的长度分别为La=18 cm、Lb=12 cm。求:

(1)每根弹簧的自然长度L0及每根弹簧的劲度系数k;
(2)若撤去弹簧b,则物块静止时物块下端离桌面的距离h。
【解析】(1)根据两弹簧弹力相等
k(La-L0)=k(L0-Lb)
得L0=15 cm
物体受力平衡
k(La-L0)+k(L0-Lb)=G
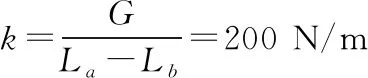
(2)若撤去弹簧b,设弹簧a的长度为L,有
k(L-L0)=G
得L=21 cm
物块离桌面距离为h=Lb-(L-La)=9 cm。
二、弹簧长度的变化问题
弹簧受力的变化与弹簧长度的变化也遵循胡克定律,即ΔF=kΔx,此时ΔF表示弹簧弹力的变化量,并不是弹簧弹力大小;此时Δx表示的是弹簧长度的改变量,并不是形变量。
【例2】如图2所示,劲度系数为k1的轻质弹簧两端分别与质量为m1、m2的物块1、2拴接,劲度系数为k2的轻质弹簧上端与物块2拴接,下端压在桌面上(不拴接),整个系统处于平衡状态。现将物块1缓慢地竖直上提,直到下面那个弹簧的下端刚脱离桌面。在此过程中,物块2的重力势能增加了多少?物块1的重力势能增加了多少?
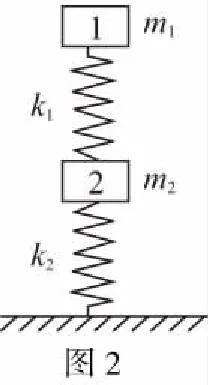
【解析】由题意可知,弹簧k2长度的增加量就是物块2的高度增加量,弹簧k2长度的增加量与弹簧k1长度的增加量之和就是物块1的高度增加量。
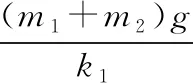
三、弹簧多解问题
弹簧可以伸长也可以被压缩,因此弹簧的弹力具有双向性,即弹力既可能是推力又可能是拉力,这类问题往往有多解。
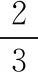
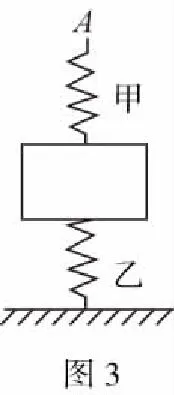
【解析】乙弹簧的末状态应分压缩和拉伸两种情况:
1.乙弹簧被压缩
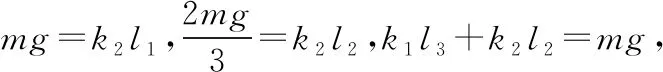
2.乙弹簧被拉伸

【点评】以上这类题是高中阶段常见题型,在求解过程中,一般由平衡条件、牛顿运动定律与弹力相联系,再结合F=kx求解。
表达式F=kx中,若x可指弹簧形变量,则相应的F指弹簧弹力;x也可指弹簧形变量的变化量,则相应的F指弹簧弹力的改变量;还有x可正可负,相对的F的大小相等但方向不同,即弹簧可被拉伸也可被压缩。所以在分析求解过程中,一定要明确x(或F)的含义、方向等。
四、弹簧串、并联组合
弹簧串、并联与电路电阻的串、并联类似,弹簧串、并联后新组合弹簧劲度系数会发生变化。
弹簧串、并联的特点:弹簧串联时,每根弹簧的弹力相等,与弹簧原长无关;原长相同的弹簧并联时,每根弹簧的形变量相等。
【例4】如图4所示,在水平面上运动的小车内,有一质量为m的物块与两根劲度系数分别为k1、k2的轻弹簧连接,小车向右以大小为a的加速度做匀加速直线运动。已知两根弹簧的形变量总和为Δx,不计物块与小车间的摩擦。则图中物块的加速度a为多少?
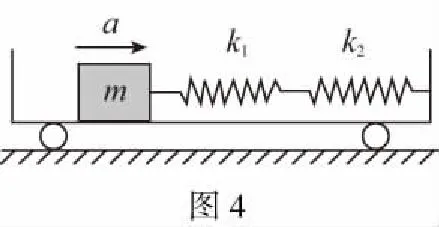
【解析】物块与小车的相对位移为两弹簧形变量之和,设相对位移为Δx,弹簧k1的形变量为Δx1,弹簧k2的形变量为Δx2,则有Δx1+Δx2=Δx
对k2:k1Δx1=k2Δx2
对物块:k1Δx1=ma

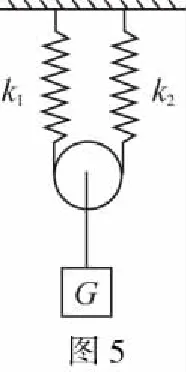
【例5】如图5所示,两个劲度系数分别为k1、k2的轻弹簧竖直悬挂,下端用光滑细绳连接,并有一光滑的轻滑轮放在细线上;滑轮下端挂一重为G的物体后滑轮下降,求滑轮静止后重物下降的距离。

【例6】如图6甲所示,一根大轻弹簧内套有一根小轻弹簧,大弹簧比小弹簧长0.1 m,它们的下端固定于地面上,上端自由,当用力压缩此组合弹簧时,测得压力与压缩距离之间的关系如图6乙所示,两根弹簧的劲度系数k1、k2分别是多少?
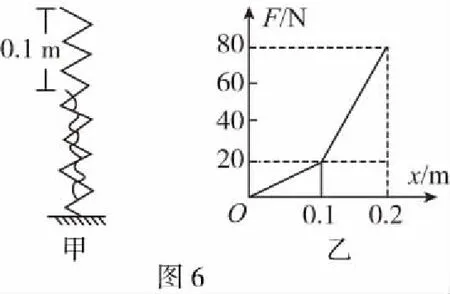
【解析】大弹簧劲度系数为k1,小弹簧劲度系数为k2,依据ΔF=kΔx得
在0~0.1 m内:20 N=k1×0.1 m
在0.1~0.2 m内:小弹簧的压缩量比大弹簧小0.1 m
80 N=k1×0.2 m+k2×0.1 m
解得k1=200 N/m,k2=400 N/m。
【点评】对于弹簧串、并联问题,首先要分析清楚弹簧连接方式,即找出各弹簧之间的弹力、形变量等关系,找出物体位移与弹簧形变量之间关系,再结合F=kx以及其他知识求解。
五、弹簧弹力突变
弹簧弹力与弹簧的形变量有关,由于弹簧两端一般与物体连接,因弹簧形变过程需要一段时间,其长度变化不能在瞬间完成,因此弹簧的弹力不能在瞬间发生突变。即可以认为弹力大小和方向不变,与弹簧相比较,轻绳和轻杆的弹力可以突变。
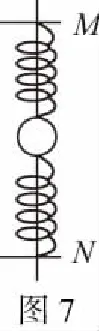
【例7】如图7所示,竖直光滑杆上套有一个小球和两根轻弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态。设拔去销钉M瞬间,小球加速度的大小为12 m/s2。若不拔去销钉M而拔去销钉N瞬间,小球的加速度可能是(取g=10 m/s2)
( )
A.22 m/s2,竖直向上 B.22 m/s2,竖直向下
C.2 m/s2,竖直向上 D.2 m/s2,竖直向下
【解析】设小球的质量为m,向上为正方向,刚开始受力平衡,则有FN+FM-G=0,拔去销钉M瞬间有FN-G=±12m,所以FN=-2m或22m,FM=12m或-12m,拔去销钉N瞬间,小球受M弹簧和重力G的作用,FM-G=ma,解得加速度a=2 m/s2或-22 m/s2,故选BC。
【点评】当弹簧形变量较大时,弹簧弹力只能发生渐变。所以,对于弹簧突变问题,一般认为弹簧弹力瞬间不变。但如果将弹簧两端的连接物体或力撤销瞬间,弹簧弹力将变为0。
在求解这类弹簧突变问题,要分析清楚突变前、后物体受力情况的变化,包括力的大小,方向的变化,而弹簧弹力大小和方向不变,结合F=kx以及其他知识求解。
六、弹簧弹力与牛顿运动定律相结合
弹簧模型是高中物理中一个重要模型,可与物理中的诸多知识点结合来,这里将弹簧弹力与牛顿运动定律相结合,来考查分析能力和推理能力。
【例8】用如图8所示的装置可以测量汽车在水平路面上做匀加速直线运动的加速度。该装置是在矩形箱子的前、后壁上各安装一个由力敏电阻组成的压力传感器。用两根相同的轻弹簧夹着一个质量为2.0 kg的滑块,滑块可无摩擦的滑动,两弹簧的另一端分别压在传感器a、b上,其压力大小可直接从传感器的液晶显示屏上读出。现将装置沿运动方向固定在汽车上,传感器b在前,传感器a在后,汽车静止时,传感器a、b的示数均为10 N(取g=10 m/s2),

(1)若传感器a的示数为14 N、b的示数为6.0 N,求此时汽车的加速度大小和方向。
(2)当汽车以怎样的加速度运动时,传感器a的示数为零。
【解析】传感器上所显示出的力的大小,即弹簧对传感器的压力,据牛顿第三定律知,此即为弹簧上的弹力大小,亦即该弹簧对滑块的弹力大小。
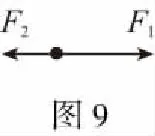
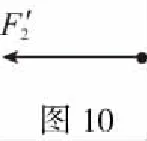
(1)如图9所示,选滑块为研究对象,依题意:左侧弹簧对滑块向右的弹力F1=14 N,右侧弹簧对滑块的向左的弹力F2=6.0 N,滑块所受合力产生加速度a1,根据牛顿第二定律有F1-F2=ma1,得a1=4 m/s2,a1与F1同方向,即向右。
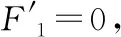
七、弹性势能
高中阶段对弹簧弹性势能的表达式不要求,但很多问题又涉及弹性势能,在求解过程中利用功能转换来求解相关问题。
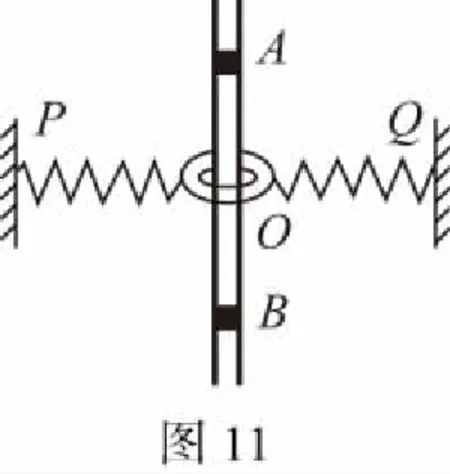
【例9】如图11所示,两根相同的轻质弹簧,中间与质量为m的圆环相连于O位置,另一端各自固定在同一水平线上的P、Q两点,弹簧恰好处于原长L,圆环套在粗糙的竖直细杆上,细杆上的A、B两点关于O点对称,OA=H。现将圆环沿杆拉至A位置由静止释放,当下滑到速度最大时,弹簧与细杆间的夹角为θ,整个过程中,弹簧处于弹性限度范围内。重力加速度为g。求:
(1)圆环过O点时的加速度;
(2)圆环过B点的瞬时速度;
(3)每根轻质弹簧的劲度系数。
【解析】(1)物体下落到O点时只受重力作用,由牛顿第二定律得
mg=ma
解得a=g。
(2)圆环从A到B过程中,弹簧弹力做功为零,圆环水平方向合力为0,故不受摩擦力作用,只有重力做功,由动能定理得

(3)下落过程中,当环所受合力为零时速度最大,此时有
2Fcosθ=mg
由胡克定律得F=kΔx
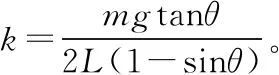
【点评】对于这类综合题,考查知识点较多,知识综合性强,在分析过程中要全面分析,分析出物体的位移与弹簧形变量之间关系,将其他知识,如牛顿运动定律、物体平衡、功能转换等,有效地与F=kx相结合求解。

