一道含洛伦兹力的动力学问题分析

广东 闵 鑫

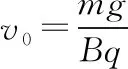
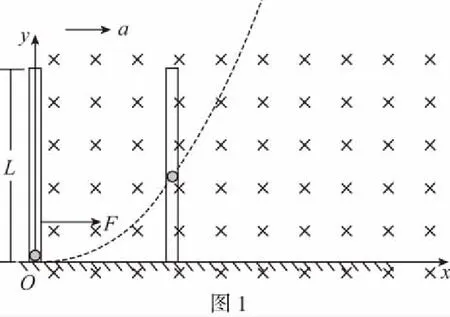
一、速度时间关系与轨迹方程

对小球在管道内运动的任意时刻t分析

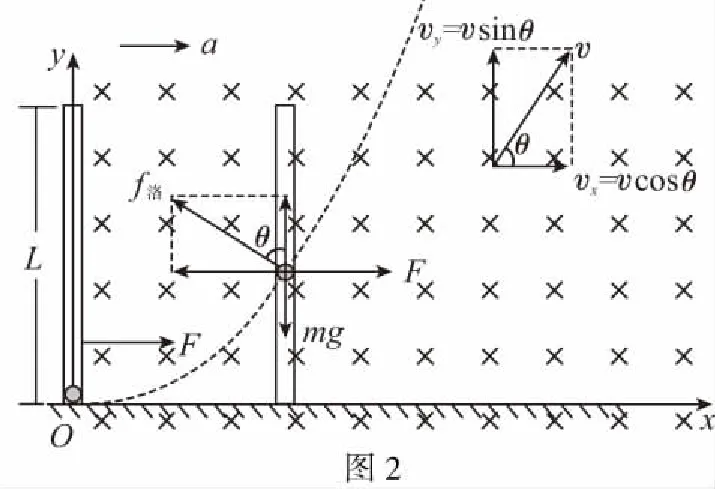
设小球速度与水平方向的夹角为θ，由题意小球水平方向速度满足

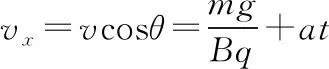
小球位置坐标(x，y)

对小球在y轴方向上由牛顿第二定律有

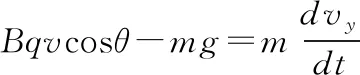
联立①③可以得到关于vy与时间t的微分方程

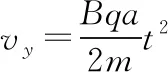
②⑤为轨迹的参数方程，联立削去t即可得到轨迹方程

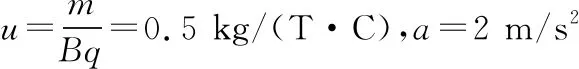
二、小球飞离塑料管道时速度的大小和方向

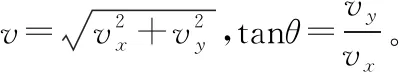
三、作用力F与时间关系、F做的功与时间关系

对小球在x方向上由牛顿第二定律

F-Bqvsinθ=ma⑥

注意到vy=vsinθ

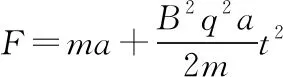
由于塑料管质量不计，拉着管道的外力大小与⑦计算相同，则

①⑦带入⑧得

重力做功与时间的关系

四、计算动能的变化以验证洛伦兹力确实没有做功

我们知道这个过程洛伦兹力总是与速度方向垂直，是不做功的！但是洛伦兹力不做功为什么小球的动能和势能都增加了呢？先看下面的计算验证

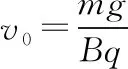
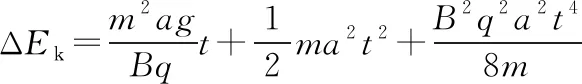
洛伦兹力确实是没有做功的！

外力F做功消耗了其他形式的能，一部分转化成了重力势能，一部分转化成了小球的动能。洛伦兹力的竖直分量做正功，水平分量做负功，总功为零。洛伦兹力的存在起到了传递能量的作用。

补充说明：洛伦兹力不做功不一定非要管道匀加速，不做功的本质原因是洛伦兹力总是与速度方向垂直。上面只是通过一个特例帮助同学们理解这一事实。

下面换一个方式来说明

取任意一小段时间Δt，在此小段时间内动能的变化

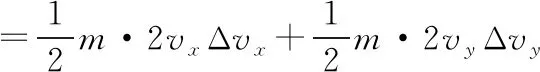
=mvxΔvx+mvyΔvy①

小球动量的变化是与洛伦兹力有关的，根据动量定理

mΔvx=(F-fx)Δt

mΔvy=(fy-mg)Δt②

由于洛伦兹力与速度垂直，如图4

fx=Bqvsinθ=Bqvy

fy=Bqvcosθ=Bqvx③

联立①②③得

ΔEk=(F-Bqvy)vxΔt+(Bqvx-mg)vyΔt

=FvxΔt-mgvyΔt

=FΔx+(-mgΔy)