Fermi气体光晶格奇摄动模型的渐近解
2018-11-28徐建中莫嘉琪
徐建中, 莫嘉琪
(1. 亳州学院 电子与信息工程系, 安徽 亳州 236800; 2. 安徽师范大学 数学与统计学院, 安徽 芜湖 241003)
0 引 言
目前, 玻色-爱因斯坦凝聚(BEC)理论已得到广泛关注[1]. 对光晶格Fermi气体及其凝聚体特性的研究也有许多结果, 包括波的演化, 量子的相变情形, 用共振技巧控制光晶格的性态, 超流与绝缘变, 光晶格Fermi气体常规超导体超导电性的微观现象(BCS)和BEC间过渡的隧穿性态、 Josephson效应、 Bloch振荡以及由相平面分析与周期性调制研究BCS[2-15]等. Landau-Zener隧穿效应为Fermi凝聚体量子现象, 是系统相邻能级间的一种量子隧穿[11]. 文献[16-27]用解析方法研究了相关的非线性问题. 本文利用奇摄动理论和方法给出一类关于Fermi气体光晶格扰动系统解的近似表示式.
研究光晶格凝聚时, 当Fermi气体的光晶格尺度相对较小且温度较低时, Fermi气体分子体系在渡越时的动力学行为可用如下Schrödinger方程描述:
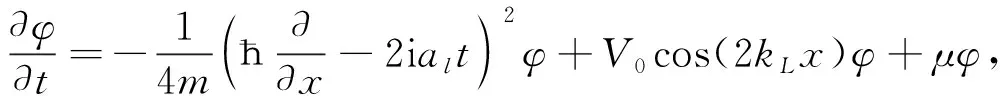
这里:x是空间变量;t是时间变量;φ是波函数;kL,μ,ħ,m,al,V0的意义可参见文献[12-13]. 在从BCS区到unitarity区过渡的化学势Schrödinger方程可表述为相位s和布局数差r的奇摄动光晶格凝聚Fermi气体系统:
其中;ε>0为小参数;a,b,c1,c2为相应物理量的无量纲数值.
1 光晶格系统模型轨线的外部解
考虑如下奇摄动Fermi气体光晶格轨线方程扰动模型:
其中:ε>0为摄动参数;f(ε,r,coss)为充分光滑的有界扰动函数, 且存在正常数δ, 满足fp(ε,r,p)≤-δ.
首先求奇摄动Fermi气体光晶格扰动模型(3)-(4)轨线的外部解. 设
(5)
将式(5)代入式(3), 合并ε的同次幂, 并令ε各次幂的系数为零. 当ε0的系数为零时, 可得奇摄动Fermi气体光晶格在退化情形的轨线方程:
(6)
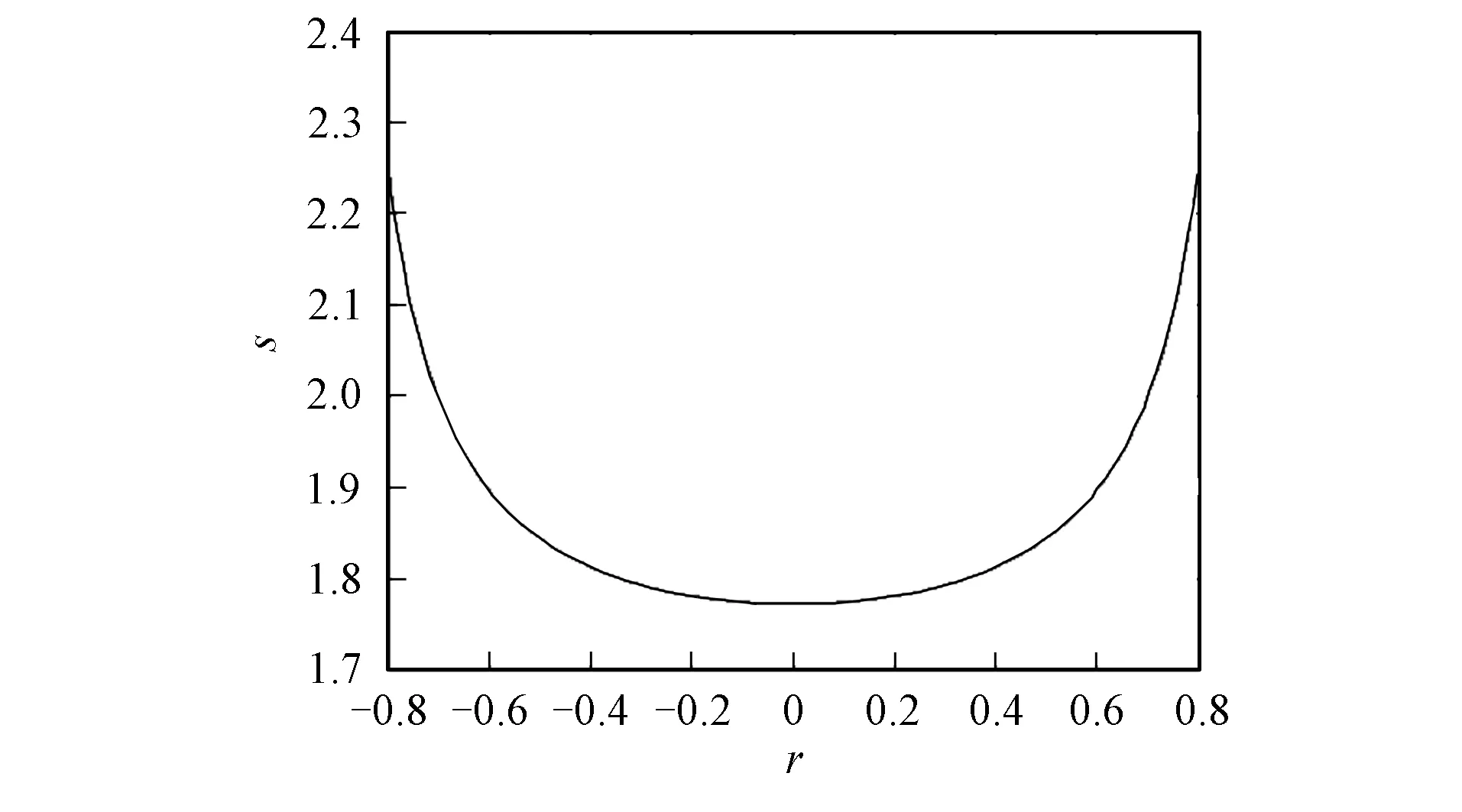
图1 光晶格退化情形下奇摄动Fermi气体的轨线Fig.1 Trajectory of a singular perturbation Fermi gases in the case of optical lattices degeneration
选取无量纲参数b=10,c1=c2=1,f=-coss, 则奇摄动Fermi气体光晶格退化情形轨线的解在相平面r,s上的闭轨线曲线如图1所示.
将式(5)代入式(3), 合并ε的同次幂, 当ε1的系数为零时, 可得
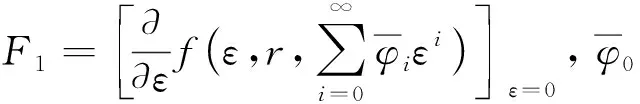
(7)
将式(5)代入式(3), 合并ε的同次幂, 当εi(i=2,3,…)的系数为零时, 可得
(8)
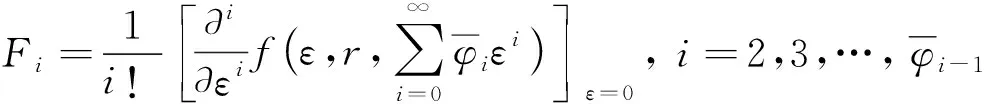

2 模型轨线的层型校正项
设奇摄动Fermi气体光晶格扰动模型(3)-(4)轨线的层型校正项ψ为
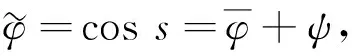
(9)
做伸长变量变换[28-29]
ξ=|r|/ε.
(10)
再设
(13)
将式(13)代入式(10),(11), 按ε的幂展开, 合并εi(i=0,1,…)项的系数并分别取为零, 依次可得:
其中:
由模型(14)-(15)和模型(16)-(17)可依次求出ψi(ξ)(i=0,1,2,…). 再将其代入式(13), 即可得奇摄动Fermi气体光晶格扰动模型(3)-(4)轨线的层型校正项ψ. 最后, 由式(9), 可得奇摄动Fermi气体光晶格扰动模型(3)-(4)轨线的渐近展开式:
(18)
3 渐近展开式的一致有效性
定理1对于奇摄动Fermi气体光晶格扰动轨线方程模型(3)-(4), 其中ε>0为摄动参数,f(ε,r,coss)为充分光滑的有界扰动函数, 且存在正常数δ, 满足fp(ε,r,p)≤-δ, 则奇摄动扰动模型(3)-(4)轨线的渐近展开式(18)为在-1 证明: 首先做如下辅助函数: α(ε,r,s)=Ym-λεm+1,β(ε,r,s)=Ym+λεm+1, -1 (19) α(ε,r,s)≤β(ε,r,s), -1 (20) 由式(15),(17)易见, 存在足够大的正常数λ0, 使得 (21) (22) 下面证明如下不等式成立: (23) (24) 事实上, 由假设知, 对于足够小的ε>0, 存在正常数M, 使得 当选取λ>M/δ时, 不等式(23)成立. 同理可证不等式(24)也成立. 由式(20)~(24)及微分不等式理论[28-29]可知,α(ε,r,s)≤β(ε,r,s)成立; 再由式(19)知, 扰动模型(3)-(4)轨线的渐近展开式(18)为在-1 选取无量纲参数a=c1=c2=1,b=10,s0=2, 扰动函数f(ε,r,coss)=-coss, 此时奇摄动Fermi气体光晶格扰动轨线方程模型(3)-(4)为 其中ε>0为摄动参数. 先求奇摄动Fermi气体光晶格扰动模型(25)-(26)轨线的外部解. 将式(5)代入式(25), 合并ε的同次幂, 并令ε各次幂的系数为零. 当ε0的系数为零时, 可得 于是有 (27) (28) 由式(5),(27),(28), 可得奇摄动Fermi气体光晶格扰动模型(25)-(26)轨线外部解的一次渐近展开式: 下面求奇摄动Fermi气体光晶格扰动模型(25)-(26)轨线的层型校正项ψ. 将式(13)代入式(25),(26), 按ε的幂展开, 合并εi(i=0,1,…)项的系数并分别取为零, 依次可得: 由模型(30)-(31)和模型(32)-(33), 可分别得: 从而可得奇摄动Fermi气体光晶格扰动模型(25)-(26)轨线层型校正项的一次渐近展开式: 结合式(29),(36), 可得奇摄动Fermi气体光晶格扰动模型(25)-(26)轨线在-1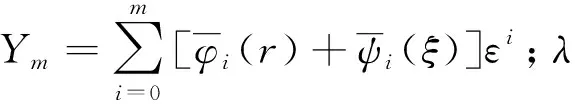
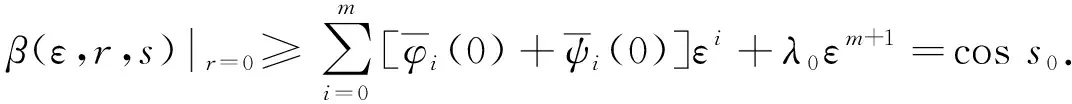

4 实 例

