一种基于凸优化的WSN障碍环境下定位算法

程 超, 李 萌, 王久赫, 陈碧龙

(长春工业大学 计算机科学与工程学院, 长春 130012)

无线传感器网络(wireless sensor network, WSN)以其设置的灵活性、 大规模、 无中心自组织、 动态性、 以数据为中心等特点广泛应用于许多领域, 形成了新的信息传递、 处理、 应用模式, 实现了物联网技术与真实物理世界的结合. 由于传感器节点常分布在不便于数据收集与传输的复杂环境或目标位置不断移动的区域, 需要通过协作方式收集、 传递及处理网络通信范围内目标的数据信息, 因此在无线传感器网络中的节点位置信息成为不可缺少的重要内容. 如何使节点的位置计算更接近实际已成为目前无线传感器网络定位研究的热点.

目前, 定位算法主要有两种： 基于测距的定位算法和无需测距定位算法. 基于测距的定位算法主要包括基于到达角度(angle of arrival, AOA)[1]的定位算法、 基于到达时间(time of arrival, TOA)[2]的定位算法、 基于到达时间差(time difference of arrival, TDOA)[3]的定位算法以及基于信号接收强度指示(received signal strength indicator, RSSI)[4]的定位算法. 无需测距的定位算法主要包括质心算法[5]、 APIT(approximate point-in-triangulation test)算法[6-7]以及DV-hop(distance vector-hop)算法[8-9]等. 两类算法相比, 综合能耗、 成本、 便捷性等多方面因素考虑, 无需测距定位即可满足人们需求的DV-hop算法应用较广泛.

传统的DV-hop算法存在未知节点定位与实际位置偏差较大的问题, 这是由于节点随机分布或定位环境复杂而使计算方法存在误差所致. 针对DV-hop算法的不足, 文献[10-12]提出了相应的改进算法. 文献[10]利用最小均方差原理, 通过修改指数值改进平均跳距, 提出了最佳指数值概念, 从而进一步提高了定位精度; 文献[11]提出了一种基于RSSI 测距技术的平均跳距计算方法, 对超过通信半径外的节点平均跳距利用锚节点间距离的误差值修正; 文献[12]也对平均跳距进行改进, 通过对节点通信半径的研究, 对节点信息传播的跳数进行修改, 达到提高定位精度的目的. 虽然这些改进方法在一定程度上提高了定位精度并减少了定位误差, 但仍存在一些不足. 如没有提到在定位环境中存在障碍物导致传播的跳数与实际不符的问题. 因此, 如何减小因定位环境中存在障碍物导致跳数对计算产生的影响, 进一步提高定位精度是本文改进算法的目标.

1 DV-hop定位算法

1.1 算法描述

传统的DV-hop算法作为一种典型的与距离无关的定位算法, 其主要内容可概述为： 首先, 网络中的每个节点以洪范的方式通过距离矢量路由获得锚节点的最小跳数及每个锚节点的坐标数据信息. 其次, 计算锚节点的平均跳距并将其广播到网络. 将未知节点接收锚节点的平均跳距作为其平均跳距, 未知节点和锚节点之间的跳距d通过将平均跳距和跳数相乘估计, 计算公式为

其中: (xi,yi),(xj,yj)为锚节点i,j的坐标; Hopsizei为锚节点的平均跳距;hij为锚节点i与j之间的跳数(i≠j);h为锚节点与未知节点之间的跳数;d为未知节点与锚节点之间的估计距离. 最后, 基于锚节点的位置坐标信息及至少3个锚节点到未知节点的距离值, 使用三边测量方法或最大似然估计方法计算未知节点坐标. 如对未知节点坐标使用三边测量方法： 设未知节点的坐标为(x,y), 锚节点的坐标为A(xa,ya),B(xb,yb),C(xc,yc), 未知节点距离3个锚节点的跳段距离分别为da,db,dc, 则

(3)

未知节点的坐标为

(4)

1.2 算法分析

传统DV-hop定位算法存在许多不足, 在实际应用中受多种环境因素影响. 例如： 由于节点分布的随机性, 算法的定位效果受网络连通度影响； 锚节点的平均跳距作为网络全局节点的平均每跳跳距, 使得计算存在误差； 算法将未知节点与锚节点之间的跳段路径长度作为它们之间的距离, 但事实上, 未知节点与锚节点的跳段路径是直线的概率很低, 导致计算存在误差, 以致于最终定位结果不准确. 因此如何减小定位方法的误差, 提高定位结果的精度, 使WSN定位算法在实践中更好地运用, 是本文改进定位算法研究的重点.

2 改进算法

传统DV-hop算法的计算是在较理想条件下进行的, 但实际中由于节点随机分布, 且传播过程中可能因存在物体阻碍使两节点的信息不能直线传播等原因, 导致计算结果与实际不符, 使得对目标定位产生较大偏差. 如图1所示,A,B,D是锚节点, 其中d是A和B之间的实际距离, 因为A和B之间信息传播理论上只需要两跳, 但由于存在障碍物, 实际上A需要3跳才能把信息传播到B, 因此如果按照传统的算法计算就会产生误差. 传统的DV-hop算法在应对类似较复杂环境下进行定位的情况并不适用, 如果在定位计算中直接用传统方法计算节点位置, 会导致较大的误差. 针对上述问题, 本文改进算法引入了一个误差修正值p：

其中：d是锚节点间的真实距离;R是节点的通信半径;hAB和HAB分别是锚节点A和B间的实际跳数和理论最小跳数. 理论最小跳数是在直线传播且平均跳距是通信半径R时的跳数.p反映了实际传播跳数偏离理论直线传播最小跳数的误差程度, 超过该误差范围时, 在计算平均跳距时就会产生较大误差, 由于误差的逐步积累, 导致在计算未知节点位置时产生较大偏离. 由文献[13]知, 当p=0.3时, 锚节点i的平均跳距为

(7)

锚节点i与j之间的估算距离为

×hij,

(8)

锚节点i与j之间的直线即实际距离为

(9)

当网络中存在N个锚节点时, 计算锚节点i的平均跳距误差εi为

(10)

-eη×εi,

(11)

其中η<0为参数变量, 具体取值随网络环境变化而不同, 本文取η=-0.5[14]. 锚节点将Ci向整个网络广播, 从而未知节点S到锚节点i之间的跳段距离可表示为

diS=Ci×hiS.

(12)

为了获得图1中未知节点C的坐标, 本文改进算法在考虑了锚节点的信息传播受物体阻碍的情况下, 对节点的平均跳距进行优化改进计算. 并且在求解未知节点到锚节点之间的距离时, 因为节点B,C,D不共线,dBC,dBD,dCD三边将构成三角形, 所以可根据三角函数原理求得dCD. 近似用三边的跳数比表示三边的关系, 得出如下关系式:

(13)

其中:α表示BC与BD两条边的夹角;H1表示节点B,C之间的跳数;H2表示节点B,D之间的跳数;H3表示节点C,D之间的跳数;dBD表示锚节点B,D之间的距离;H1,H2,H3均为可确定的数值. 又因为未知节点C到最近的锚节点B之间的跳段距离dBC可通过式(12)求得, 所以计算可得

因此, 本文改进定位算法在考虑到节点间数据信息传播受阻碍的情况下, 先改进节点B,C之间的距离计算方法, 再结合锚节点B,D间的准确距离, 共同计算未知节点C到锚节点D之间的距离. 同理, 可求得其他未知节点到最近锚节点的距离, 进而最终求得未知节点的坐标. 本文算法结合实际, 考虑了当无线信号传播被阻挡时如何减小其对计算造成的误差, 以及进一步对求未知节点到锚节点跳段距离时, 两锚节点间的准确距离对其的校正. 为了更好地定位未知节点位置, 可对计算出的未知节点坐标进行优化处理. 本文对改进算法中的未知节点坐标进行凸优化处理, 优化信息传播过程, 使未知节点的坐标更接近实际位置.

3 对未知节点优化

3.1 凸优化

凸优化是指目标函数为凸函数, 且变量所属集合属于凸集的优化问题. 连接属于集合中的任意两点, 得到两点间的直线段, 若直线段上的所有点全部位于该集合内, 则称该集合为凸集. 即设集合D⊂n, 若对于任意两点x,y∈D以及实数α(0≤α≤1), 都有

αx+(1-α)y∈D,

则称集合D为凸集. 设集合S⊆n为凸集, 若满足

f((1-α)x+αy)≤(1-α)f(x)+αf(y),

(16)

则称函数f(x)是凸集S上的凸函数. 因此, 若满足：

且f(x)为定义在D(D为凸集)上的凸函数, 则该优化问题即为凸优化.

3.2 无需测距的分布式(ESOCP)优化

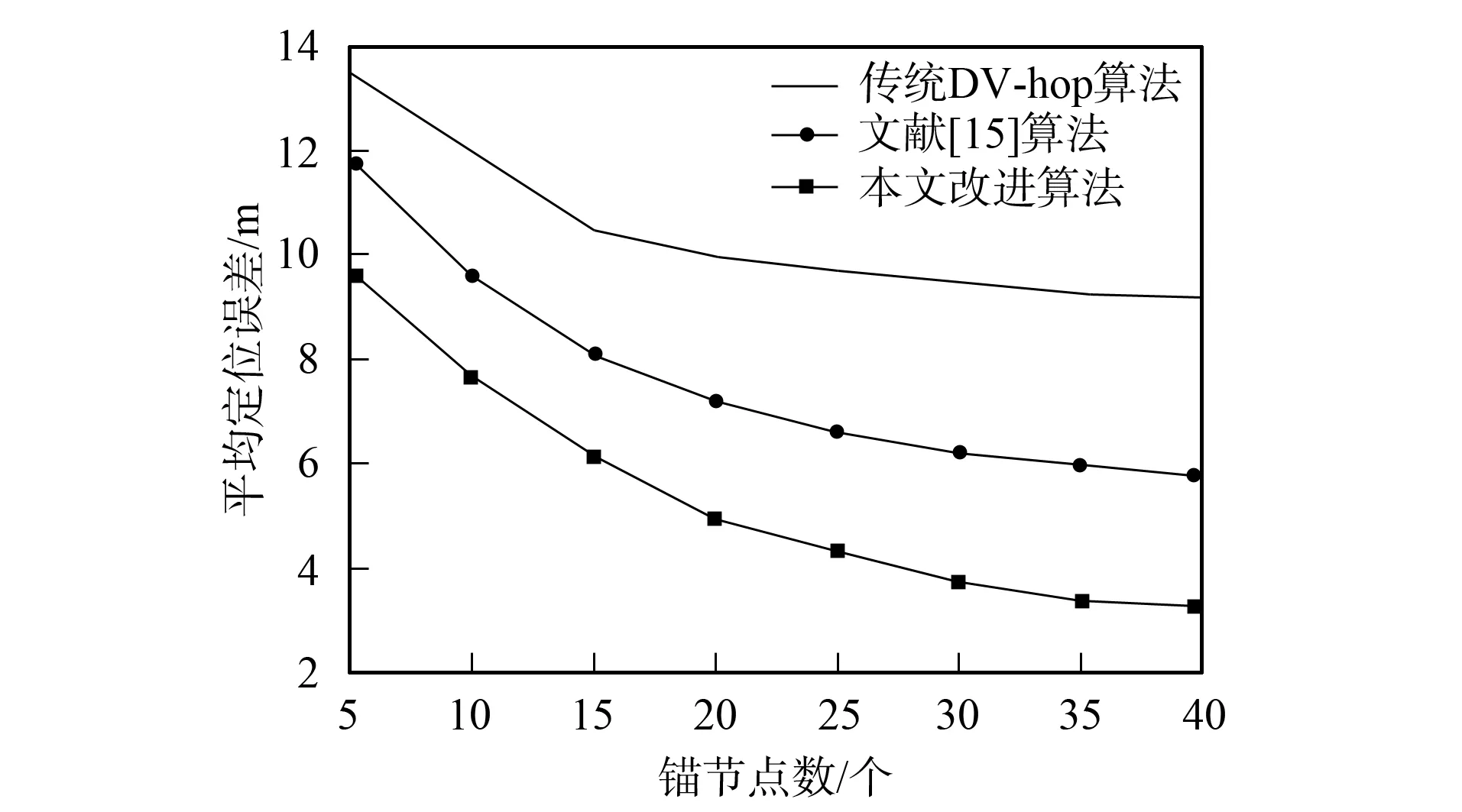
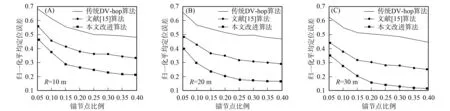
假设WSN网络中共N个节点, 有m个锚节点和(N-m)个未知节点, 且m

超出通信半径, 需一个中继节点才可通信的节点即为两跳邻居节点. 对于两跳节点i和j, 它们之间的距离满足

R<‖xi-xj‖≤2R.

相应地, 这些节点组成的集合用N2表示. 因此, 对于未知节点定位的凸优化问题, 可用公式表示为

其中S是N1和N2的集合, 若S=N1, 则0≤tij≤R2; 若S=N2, 则R2≤tij≤4R2.

根据WSN定位情况, 上述问题可转化为

(20)

设k表示优化过程中迭代的次数, 则以分布式的方式利用顺序贪婪优化算法解得：

4 仿真结果与分析

将100个节点随机部署在(100×100)m2的正方形感知区域内构成实验环境, 采用MATLAB2012a软件对传统DV-hop算法、 文献[15]算法及本文改进算法进行仿真实验, 验证算法的定位效果. 实验测试由通信半径和锚节点作为变量对不同算法定位精度的影响, 并对导致实验结果的原因进行分析. 为了降低随机产生的误差, 取得更准确的实验数据, 在同等参数条件下进行100次仿真, 取其均值作为实验结果.

(25)

归一化平均定位误差为

(26)

图2 锚节点数对定位误差的影响Fig.2 Effects of number of anchor nodes on positioning error

图2为在相同实验环境下, 通信半径不变而锚节点增加时, 传统DV-hop算法、 文献[15]算法及本文改进算法的仿真结果. 由图2可见, 当节点通信半径不变时, 3种定位算法的平均定位误差均随锚节点增多而降低, 且相互之间的差距越来越大, 这是由于WSN网络中锚节点的增多不仅直接影响算法的定位精度, 且信息传递路径可通过锚节点而使得其趋于直线的概率增大, 减少了数据传播过程中还需计算跳段距离导致的误差. 本文改进算法相比于传统DV-hop算法和文献[15]算法, 总体上实现了在不增加额外支出的条件下, 达到提高定位精度的目的.

在相同条件下, 节点通信半径和锚节点个数逐渐增大时, 传统DV-hop算法、 文献[15]算法及本文改进算法的仿真结果如图3所示. 由图3可见, 传统DV-hop算法和文献[15]算法与本文改进算法在相同锚节点个数下, 定位误差之间的差距随通信半径的增大而增大. 表明除锚节点个数外, 通信半径也能决定算法的定位效果. 这是因为随着通信半径的增大, 未知节点到锚节点的跳数减少, 数据信息从一个节点传播到下一个节点时可选择的范围变大, 能选出更合理的路由, 优化信息传播过程. 本文改进算法比传统DV-hop算法与文献[15]算法定位误差小很多. 当R=10 m时, 减少约20%和9%； 当R=20 m时, 减少约24%和11%； 当R=30 m时, 减少约30%和13%. 仿真结果表明本文改进算法定位性能最优.

图3 节点通信半径对算法误差的影响Fig.3 Effects of node communication radii on algorithmic error

综上所述, 针对传统DV-hop算法在实际应用中存在受环境影响使得定位结果偏差较大的问题, 本文提出了一种改进算法. 该算法首先考虑了在定位测试环境中存在障碍物的情况下对节点信息传播的影响, 进而改进了锚节点的平均跳距计算, 使其更适于距离的计算； 然后在此基础上结合三角函数进一步优化未知节点与锚节点距离的计算, 使最终的定位更接近真实位置； 最后对未知节点位置进行凸优化, 优化信息传播过程, 减小不合理传播导致的误差, 提高定位性能. MATLAB仿真结果表明, 本文改进算法比传统DV-hop算法具有更好的定位性能, 实现了提高WSN网络定位精度的目标.