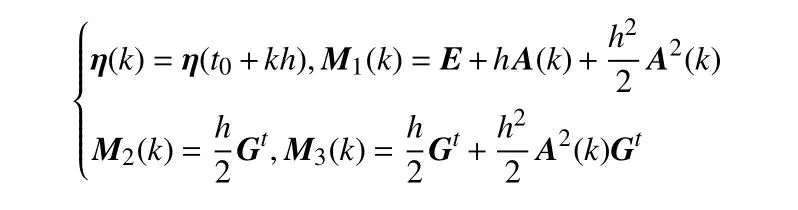时变切换时滞反馈镇定混沌系统不稳定周期轨线1)

曾尖尖 郑远广

(南昌航空大学数学与信息科学学院,南昌 330063)

引言

混沌是非线性系统中普遍存在的一种动力学现象,其典型的特征是对扰动的敏感性和不可预测性.在许多实际工程系统中,混沌常常是有害的.生态系统中的混沌会导致物种的突然消亡[1-2];被动行走机器人中的混沌会降低行走效率,同时增加能量消耗[3-4];网络信息传输中的混沌会导致网络堵塞[5].因此,混沌控制是一项重要的研究课题[6-7].在早期的研究中,人们常常通过改变系统的分叉参数[8]来达到消除混沌的目的,或者用外部周期信号去同步混沌系统,从而引导混沌系统到期望的周期运动上来.采用这些控制方法控制混沌时,受控系统的周期解轨线并不是原系统的混沌吸引子中包含的轨线,因此,通常需要比较大的控制力和比较大的能量消耗.

由于混沌吸引子中包含无数个不稳定周期轨线[9],基于这一事实,人们提出了OGY 控制方法[10].当系统运动到预定的不稳定周期轨道附近时,对系统关键参数进行微小的摄动从而把系统稳定到该周期轨道上.由于该方法是把混沌系统引导到混沌吸引子中原有的不稳定周期轨道上,因此仅需要微小的控制力和少量的能量消耗.然而,OGY 控制方法对外界扰动极度敏感,当系统受到扰动远离预定的周期轨道运动时,该方法无法实施.为了克服这一缺点,人们提出了时滞反馈控制(DFC)[11].DFC 用系统输出状态信号和输出状态信号的适当滞后值之差生成反馈控制信号,其中的时滞量设置成等于预定要控制的不稳定周期轨道的周期.当受控周期轨道稳定后,DFC 的控制信号消失,因此DFC 不会改变原系统的周期轨道,仅改变其稳定性.在使用DFC 对混沌系统进行控制时,不需要知道系统精确的数学模型,只需要测得目标周期轨道的周期.DFC 使用方便,且具有较好的控制效果,在实际工程中得到广泛的应用[12-14].

在经典DFC 的使用中,人们发现该方法存在一定的局限性.比如,DFC 存在奇数限制(ONL)[15].ONL 表明DFC 不能稳定具有奇数个实部大于零的条件Lyapunov 指数的周期轨线.此外,用DFC 稳定某些不稳定周期轨线时,受控周期轨线常常具有比较小的稳定区域[16].这里的稳定区域是指参数空间的某个区域,当控制参数在这个区域中取值时,受控周期轨线是稳定的.为了提高经典DFC 的控制效果,人们对该方法进行了多方面的改进[16-18].比如,人们提出了半周期延迟反馈控制来避免DFC 的奇数限制[19];文献[20]基于梯度下降法设计了一种自动调整反馈增益的方法,该方法可以有效地确定稳定目标周期轨线的反馈增益系数;为了稳定高周期的不稳定周期轨线,文献[16]提出了广义时滞反馈控制方法(EDFC).

切换控制策略在控制工程中得到广泛应用[21-23].Bang-bang 控制的控制信号在两个常值之间切换[24],该方法能够实现最短时间控制.滑模控制是另一种常用的切换控制技术.滑模控制的主要思想是,通过不连续地切换控制信号,使受控系统到达并保持在设定的滑模面上,从而把系统稳定到期望的平衡状态[25].在系统耦合同步中,切换策略也被用来改变系统的耦合方式以提高系统的同步能力[26].周期耦合是一种依赖于时间和切换频率的耦合方式[27-28],只有在特征的时间段上,系统之间存在耦合,而在其他时间段上,系统之间不存在耦合.研究表明,具有适当切换频率的周期耦合系统同步性能要显著优于标准耦合系统的同步性能[26].为了理解周期耦合对同步流形稳定性的影响,文献[29]通过计算同步流形的局部条件Lyapunov 指数,发现周期耦合以一种非线性的方式修正了同步流形的稳定性.

在混沌控制的工程实践中,受控系统常常存在某些不确定性因素,同时控制参数也会受到一定的限制.要实现对目标周期轨线的稳定控制,就需要受控周期轨线具有足够大的稳定区域.因此,采用适当的方法进一步扩大受控周期轨线的稳定区域具有重要的工程实践意义.本文基于时变切换策略[26,30]对经典DFC 控制方法进行改进,提出了时变切换时滞反馈控制方法(TSDFC).其目的是提高经典DFC 的控制效果,扩大受控周期轨线的稳定区域.本文的结构如下:在第二节中,提出时变切换时滞反馈控制方法.在第三节中,通过实例分析,研究TSDFC 的控制性能.最后在第四节中,对本文的研究工作进行总结并对相关问题进行讨论.

1 TSDFC

考虑受控的非线性系统

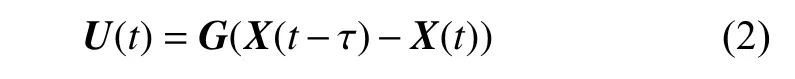
式中,G为反馈增益系数矩阵,τ为时滞.

选取系统中某个周期为T的不稳定周期轨线X*(t) 作为待镇定的目标周期轨线.DFC 是将时滞τ设定等于目标周期轨线X*(t) 的周期T,再通过调节反馈增益系数矩阵G,使受控不稳定周期轨线X*(t)达到稳定.当受控周期轨线X*(t) 稳定时,反馈控制信号U(t) 趋于无穷小.

虽然DFC 使用方便,但受控周期轨线X*(t) 常常仅有较小的稳定区域.为了提高DFC 的控制效果,扩大受控周期轨线X*(t) 的稳定区域,本文基于时变切换策略[26,30]对DFC 进行改进,提出了TSDFC.TSDFC 的反馈控制信号为

式中,反馈增益系数矩阵为

式中,s gn(x)=G为定常反馈增益系数矩阵,ω为切换频率,其决定了切换速度的快慢.TSDFC的控制信号仅在特征的时段上存在,而在其他时段控制信号不存在,即控制信号按照给定的频率 ω 进行周期性切换.

为确定受控周期轨线X*(t) 的稳定区域,求得主稳定方程为[28]

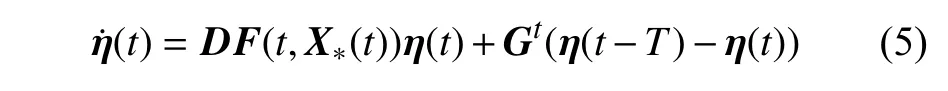
式中,η(t)=X(t)-X*(t)为偏差变量,DF(t,X*(t))为F(t,X(t))在X*(t) 上的雅可比矩阵.X*(t) 的稳定性由主稳定方程(5)的条件Lyapunov 指数确定.当主稳定方程(5)的所有条件Lyapunov 指数均具有负实部时,受控周期轨线X*(t) 稳定.

主稳定方程(5)是时滞系统,其初值状态空间是无穷维Banach 空间C=C([-T,0],Rm).在Banach 空间C中的初始函数定义为ηt0(θ)=η(t0+θ),其中,t0为初始时间,θ ∈[-T,0].系统(5)的最大条件Lyapunov指数定义为其中

由于系统(5)的初值状态空间是无穷维的,从而无法通过对系统(5) 进行积分来计算最大条件Lyapunov 指数 λm[31].为克服这一困难,本文采用Runge-Kutta 方法,将系统(5)转化成具有有限维状态空间的离散系统,进而求得最大条件Lyapunov 指数 λm[32],详细的计算过程请参考附录A.

将TSDFC 应用于系统(1)得到

当ω=0时,TSDFC 退化为DFC.

2 TSDFC 镇定不稳定周期轨线

本节用TSDFC 控制两个典型的非线性混沌系统,考察该方法镇定不稳定周期轨线的具体效果.首先,通过求得受控周期轨线X*(t) 的稳定区域与切换频率 ω 的关系图,找到最优切换频率,使受控周期轨线X*(t) 的稳定区域达到最大.其次,对比TSDFC和经典DFC 的控制效果,阐述TSDFC 在镇定混沌系统的不稳定周期轨线的有效性.

2.1 TSDFC 控制 Rössler 系统

受TSDFC 控制的 Rössler 系统方程为

式中,x,y,z为系统状态变量,a,b,c为系统参数,为反馈增益系数,其在定常值g和0之间周期切换.不失一般性,这里假设状态变量x为唯一可获得的系统状态变量,则反馈控制信号表示为Ut(t)=gt(x(t-T)-x(t)).

将系统参数设定为a=0.2,b=0.2,c=5.7,此时Rössler系统呈现混沌动力学行为,其混沌吸引子如图1 所示.

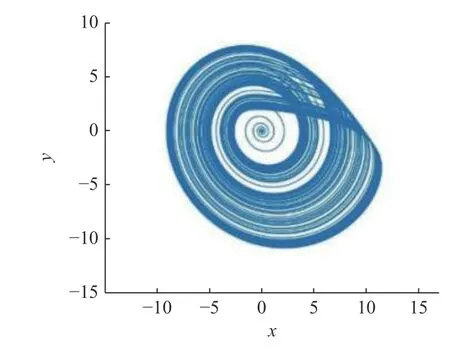
图1 Rössler 系统的混沌吸引子Fig.1 The chaotic attractor of Rössler system

选择 Rössler 混沌吸引子中两个典型的不稳定周期轨线Xk(t)=(xk(t),yk(t),zk(t))T(k=1,2) 作为待镇定的目标周期轨线.图2 展示了目标周期轨线Xk(t)在xoy平面上的投影.

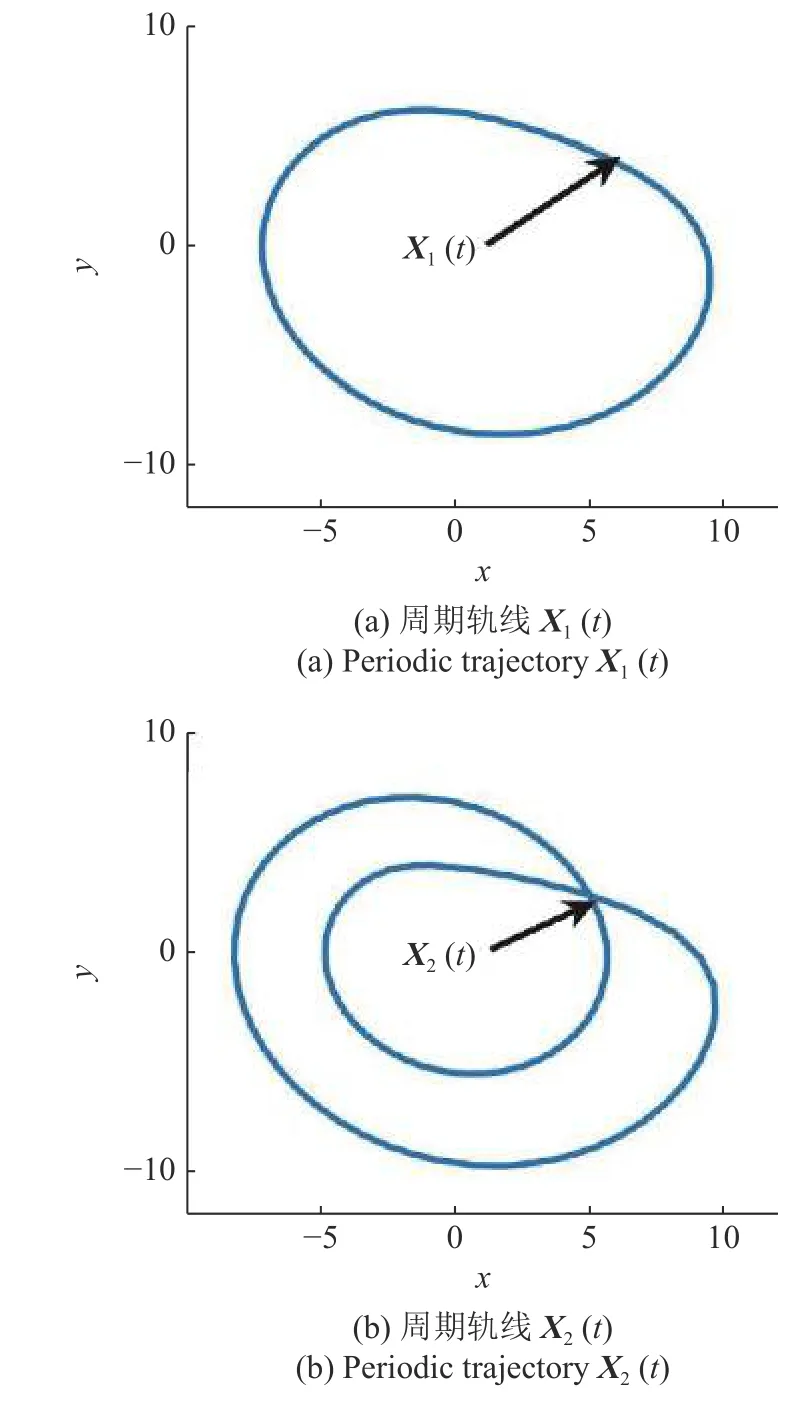
图2 Rössler 系统的不稳定周期轨线在 x oy 平面上的投影Fig.2 The projection of the unstable periodic trajectory ofRössler system on the x oy plane

为确定受控周期轨线Xk(t) 的稳定区域,求得主稳定方程为

式中,时滞 τk等于目标周期轨线Xk(t) 的周期(T1=5.880,T2=11.760).当受控周期轨线Xk(t) 的最大条件Lyapunov 指数 λm的实部小于零,受控周期轨线Xk(t) 稳定.受控周期轨线Xk(t) 的稳定区域是反馈增益系数g的某个区间,在这个区间上受控周期轨线稳定,该区间的长度记为稳定区域宽度Ws.受控周期轨线Xk(t) 的稳定区域越大表明控制效果越好.

当ω=0时,TSDFC 退化成经典DFC.通过计算受控周期轨线Xk(t) 的最大条件Lyapunov 指数,得到受控周期轨线Xk(t) 的稳定区域.图3 中红色虚线是应用DFC 镇定不稳定周期轨线Xk(t) 时的最大条件Lyapunov 指数随反馈增益系数g变化的曲线图.同时在表1 中给出了受控周期轨线Xk(t) 的稳定区域和稳定区域宽度Ws.结果表明受DFC 控制的周期轨线Xk(t) 的稳定区域较小,这表明DFC 的控制效果比较差.

为提 高经典DFC 的控制性能,令 ω >0,这时TSDFC 的控制信号将依据时段进行切换,其切换过程如图4 所示,在灰色时段上,控制信号存在,而在灰色时段之外,控制信号消失.TSDFC 的控制效果与切换频率 ω 密切相关.为确定最佳切换频率 ω,对应于周期轨线X1(t)和X2(t),分别求得各自的稳定区域宽度Ws随切换频率ω 的变化曲线(见图5).从图5 中可见,切换过程以非线性方式修改了受控不稳定周期轨线的稳定性和稳定区域[33],稳定区域宽度Ws随切换频率 ω 的增大而非平滑地变化.对应于周期轨线X1(t)和X2(t) 的最佳切换频率分别为ω1=3.9和ω2=2.2.采用最佳切换频率,求得对应于周期轨线X1(t)和X2(t) 的最大条件Lyapunov 指数随反馈增益系数g的变化曲线如图3 所示(蓝色实线),同时在表1 中给出了相应的稳定区域和稳定区域宽度Ws.

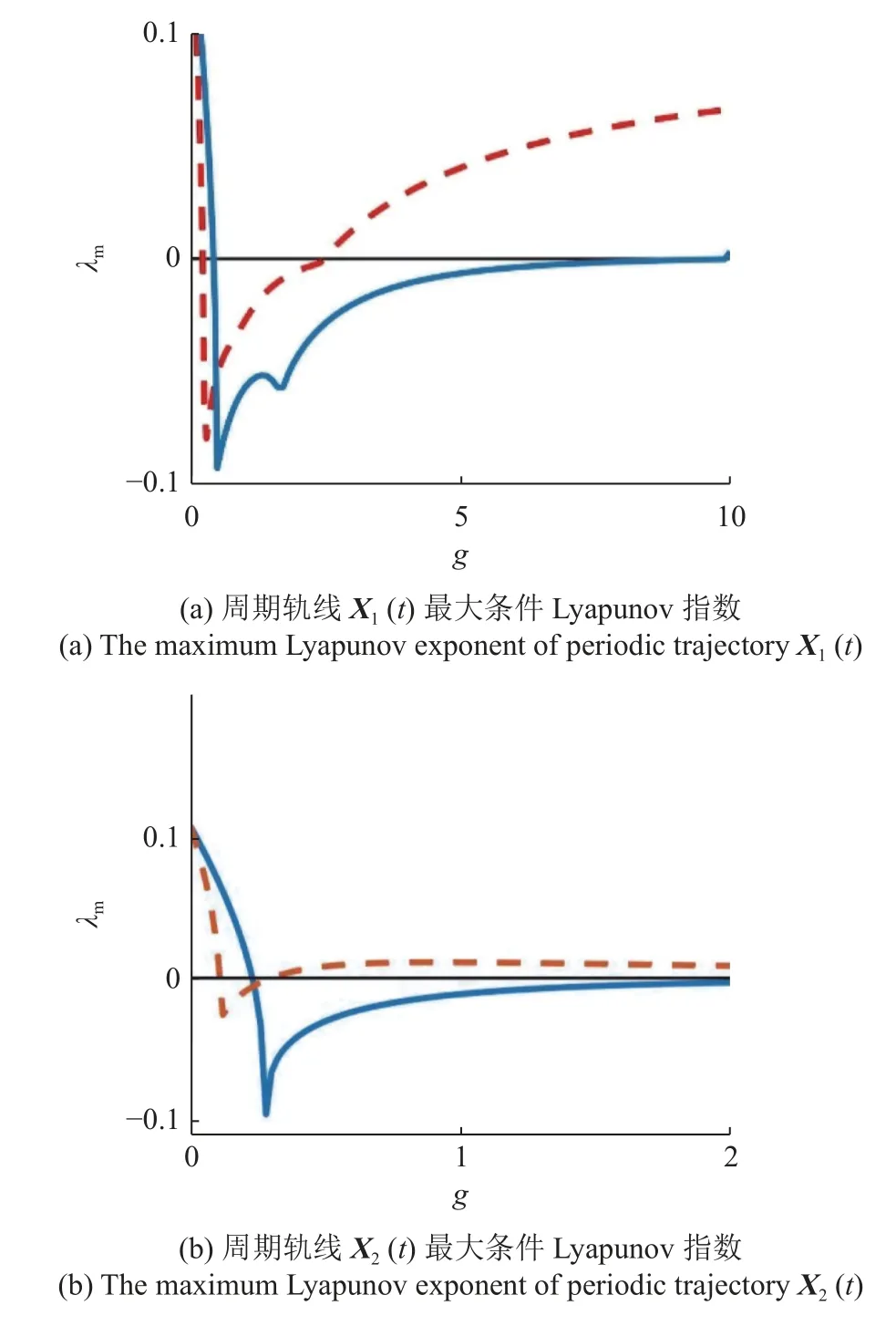
图3 受控周期轨线 Xk(t) 最大条件Lyapunov 指数随反馈增益系数g的变化曲线对比图,红色虚线和蓝色实线分别对应于DFC和TSDFCFig.3 The comparison of the maximum Lyapunov exponent of periodic trajectory Xk(t) as a function of the feedback strength,the red dotted line and the blue solid line correspond to DFC and TSDFC,respectively

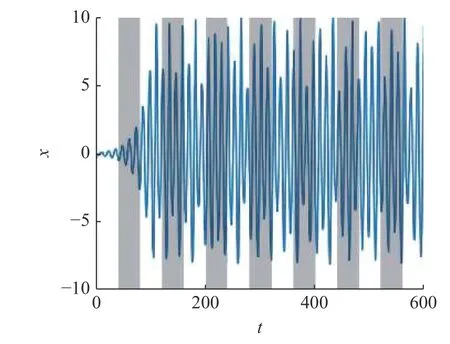
图4 系统(9)的时间序列和TSDFC 控制信号在不同时段上切换示意图,在灰色时段中控制信号存在,而在灰色时段外控制信号消失Fig.4 The time series of system(9) and the schematic diagram of the switching of TSDFC control signals in different time intervals,where the control signal exists in the gray time intervals and disappears outside the gray time intervals

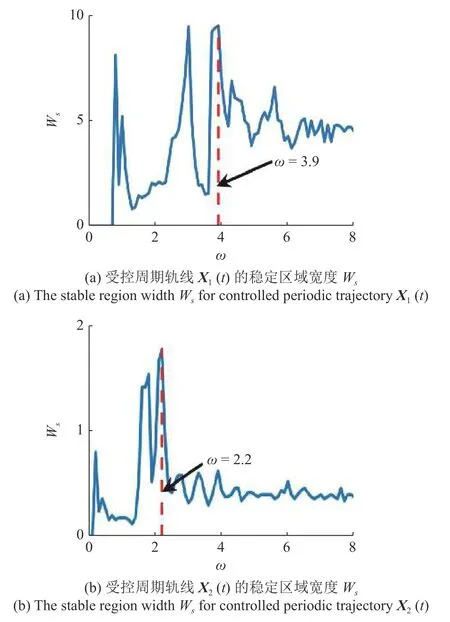
图5 受控周期轨线 Xk(t) 的稳定区域宽度 Ws随切换频率 ω 的变化曲线Fig.5 The stable region width Wsof controlled periodic trajectory Xk(t) as a function of the switching frequencyω

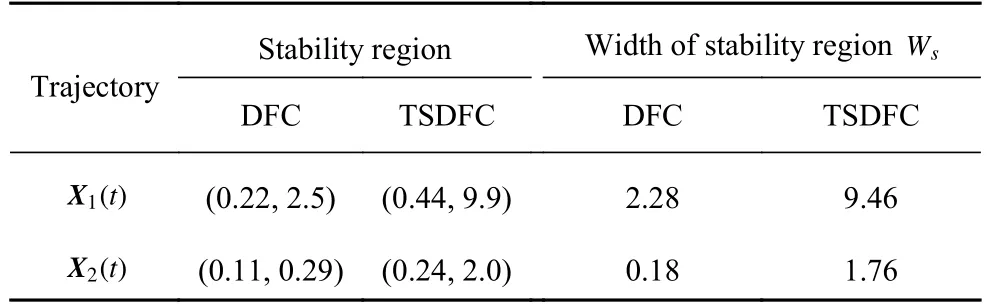
表1 受控周期轨线 Xk(t) 的稳定区域Table 1 The stability regions of the controlled periodic trajectory Xk(t)

通过图3和表1 中对比DFC和TSDFC 的控制效果,可见应用TSDFC 时受控周期轨线Xk(t) 的稳定区域明显大于应用DFC 时受控周期轨线Xk(t) 的稳定区域.因此,采用恰当的切换频率,TSDFC 的控制性能明显优于DFC 的控制性能.

为进一步检验上述结果的正确性,考察误差指数

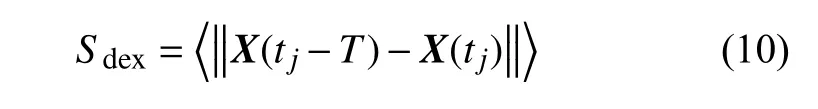
式中,X(tj)(j=1,2,···) 是系统状态变量的时间序列,〈·〉表示足够长的时间内平均值.当受控周期轨线X*(t) 稳定时,误差指数Sdex趋近于零.误差指数Sdex随反馈增益系数的变化曲线如图6 所示.从图6 中可见,图中Sdex趋近于零的区域与图3和表1 中得到的稳定区域是一致的,从而验证了图3和表1 中结果的正确性.

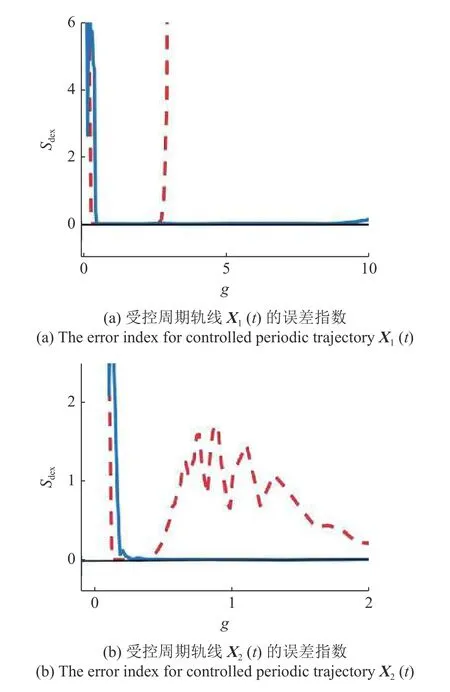
图6 受控周期轨线 Xk(t) 的误差指数随反馈增益系数 g 的变化曲线对比图,红色虚线和蓝色实线分别对应于DFC和TSDFCFig.6 The comparison of the error index of the controlled periodic trajectory Xk(t) as a function of the feedback strength g,the red dotted line and the blue solid line correspond to DFC and TSDFC,respectively

2.2 TSDFC 控制Van der Pol 系统

受TSDFC 控制的Van der Pol 系统方程为

式中,x和y为系统状态变量,µ为系统参数,a和分别表示外激励幅值和频率.反馈增益系数gt={sgn[cos(ωt)]+1}·g在定常值g和0之间周期切换.

将系统参数设定为 µ=1,a=0.998,=0.45.此时Van der Pol 系统呈现混沌动力学行为,其混沌吸引子如图7(a)所示.

选择Van der Pol 混沌吸引子中一个典型的不稳定周期轨线X3(t)=(x3(t),y3(t))T,作为待镇定的目标周期轨线.图7(b)展示了目标周期轨线X3(t)在xoy平面上的投影.

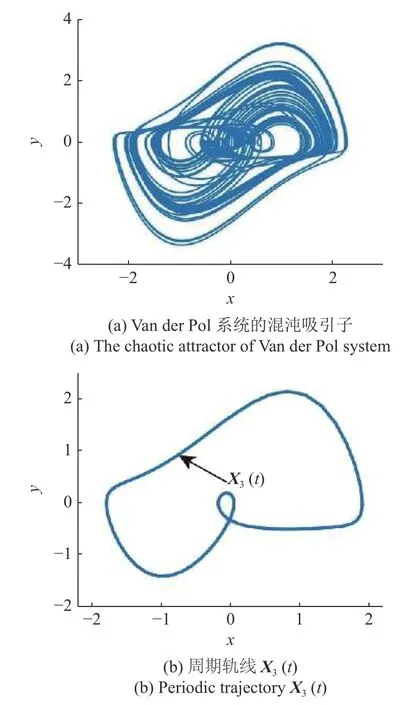
图7 Van der Pol 系统的混沌吸引子和不稳定周期轨线在 x oy 平面上的投影Fig.7 The projection of the chaotic attractors and unstable periodic trajectory of Van der Pol systems on the x oy plane

为确定受控周期轨线X3(t) 的稳定性区域,求得主稳定方程为

式中,时滞 τ3等于目标周期轨线X3(t)的周期T3=2π/.当受控周期轨线X3(t) 的最大条件Lyapunov 指数λm的实部小于零,受控周期轨线X3(t) 稳定.

当ω=0时,TSDFC 退化成经典DFC.图8 中红色虚线是应用DFC 镇定不稳定周期轨线X3(t) 时的最大条件Lyapunov 指数随反馈增益系数g变化的曲线图,同时求得受控周期轨线X3(t) 的稳定区域宽度Ws为0.88.结果表明受DFC 控制时周期轨线X3(t)的稳定区域较小,这表明DFC 的控制效果比较差.

图8 受控周期轨线 X3(t) 最大条件Lyapunov 指数随反馈增益系数g的变化曲线对比图,红色虚线和蓝色实线分别对应于DFC和TSDFCFig.8 The comparison of the maximum conditional Lyapunov exponent of the controlled periodic trajectory X3(t) as a function of the feedback strength g,the red dotted line and the blue solid line correspond to DFC and TSDFC,respectively

为了扩大受控周期轨线X3(t) 稳定区域,令 ω >0,这时TSDFC 的控制信号将依据时段进行切换.为确定最佳切换频率 ω,对于周期轨线X3(t),求得稳定区域宽度Ws随切换频率 ω 的变化曲线(见图9).从图9中可见,切换过程以非线性方式修改了受控不稳定周期轨线的稳定性和稳定区域[33],稳定区域宽度Ws随切换频率 ω 的增大而非平滑地变化,对于周期轨线X3(t) 的最佳切换频率为 ω3=5.4.采用最佳切换频率 ω3,求得周期轨线X3(t) 的最大条件Lyapunov 指数随反馈增益系数g的变化曲线如图8 所示(蓝色实线),同时也求得受控周期轨线X3(t) 的稳定区域宽度Ws为4.95.

图9 受控周期轨线 X3(t) 的稳定区域宽度 Ws随切换频率 ω 的变化曲线Fig.9 The width of the stable region of the controlled periodic trajectory X3(t) as a function of the switching frequency ω

通过图8 中对比DFC和TSDFC 的控制效果,可见应用TSDFC 时受控周期轨线X3(t) 的稳定区域明显大于应用DFC 时受控周期轨线X3(t) 的稳定区域.因此采用恰当的切换频率,TSDFC 的控制性能明显优于DFC 的控制性能.

为进一步检验上述结果的正确性,考察误差指数

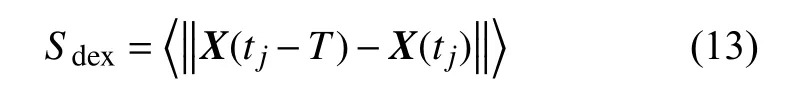
误差指数Sdex随反馈增益系数g的变化曲线如图10所示.从图10中可见,图中Sdex趋近于零的区域与图8 中得到的稳定区域是一致的,从而验证了图8 中结果的正确性.

图10 受控周期轨线 X3(t) 的误差指数随反馈增益系数 g 的变化曲线对比图,红色虚线和蓝色实线分别对应于DFC和TSDFCFig.10 The comparison of the error index of the controlled periodic trajectory X3(t) as a function of the feedback strength g,the red dotted line and the blue solid line correspond to DFC and TSDFC,respectively

总结前面的两个算例分析,我们得到以下结论.TSDFC 的控制性能与切换频率密切相关.受控周期轨线的稳定区域随切换频率的变化呈现强非线性变化.当采用恰当的切换频率时,受TSDFC控制时周期轨线的稳定区域明显大于受经典DFC控制时周期轨线的稳定区域.

备注:TSDFC 可看成是DFC 的拓展.当ω=0时,TSDFC 退化成经典DFC.虽然在本文中TSDFC仅用于稳定两个混沌系统的不稳定周期轨线,但与经典DFC 一样,TSDFC 可以应用于广泛的混沌系统控制中.

3 结论

本文首次在经典DFC 的基础上,加入时变切换策略来提高其控制性能,建立了TSDFC 方法.实例研究表明,当选择恰当的切换频率时,TSDFC 可以稳定不稳定周期轨线,且受控周期轨线的稳定区域明显大于应用经典DFC 时受控周期轨线的稳定区域.从实际应用的角度来看,相比经典DFC,TSDFC具有显著的优点.例如,在一些实际受控系统中,反馈增益系数被限制在某些有限的区域内.利用TSDFC方法时,可以选择恰当的切换频率,改变和扩大受控周期轨线的稳定区域,使反馈增益系数落入稳定区域,从而实现对周期轨线的镇定.此外,提出的TSDFC方法,开辟了另一种利用不连续控制信号来控制混沌系统的可能性.TSDFC 的控制性能取决于控制时段的选择.本文仅研究了一种比较简单的时变切换策略.对于其他更复杂的时变切换策略,TSDFC 控制效果如何？特别是哪种时变切换策略对提高经典DFC 的控制性能是最好的,目前还不清楚.这些问题值得进一步研究.

附录A 计算主稳定方程的最大条件Lyapunov 指数

对于主稳定方程

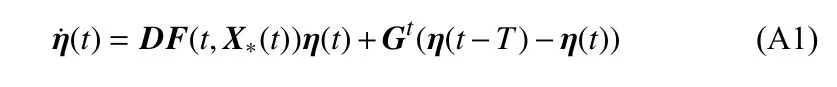
式中,η(t)∈Rm为偏差变量,T为时滞,X*(t+T)=X*(t)为待镇定的目标周期轨线,DF(t+T,X*(t+T))=DF(t,X*(t))∈Rm×m为系统矩阵.设时区[t0,t0+T] 上的时间序列为tk=t0+kh,其中k=0,1,···,kT,kT=T/h,h为步长.为减少计算最大条件Lyapunov指数的计算量,用二阶Runge-Kutta 方法将主稳定方程(A1)离散化得到

在式(A2)中