一类反应-扩散-对流方程的平衡解分析

王 燕

（南京财经大学应用数学学院，江苏南京210023）

反应扩散方程一般用来描述生物种群或化学物质的扩张和传播问题.在实际情况中由于受到各种环境因素的影响, 这种扩张行为往往具有某种方向性[1-2], 可用方程中的对流项来刻画这种具有方向性的移动[3-5].文献[6]分析了方程(1)的自由边界问题(这里反应项f(u)为Fisher-KPP类型):

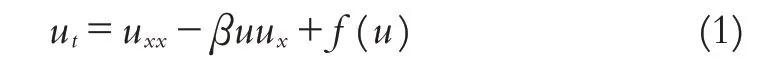
其中u=u(t,x), t ＞0, x ∈I ⊆ℝ, β ＞0, 得到了解的全局存在唯一性、扩张灭亡二分性以及渐近扩张速度的估计.若考虑反应项f(u)是双稳态型时的自由边界问题, 则其中判断问题的解是否收敛于某一个平衡解是非常基础而关键的一个问题, 因此本文讨论当f是双稳态型非线性项时方程(1)的平衡解类型.

1 问题描述

由于方程来自生态模型或化学模型, 其中u 表示物质的密度, 故由解u的非负有界性, 只研究方程(1)的非负有界平衡解,即下述方程的非负有界解:

其中v=v(x),x ∈I ⊆ℝ.

方程(2)等价于如下二维系统:

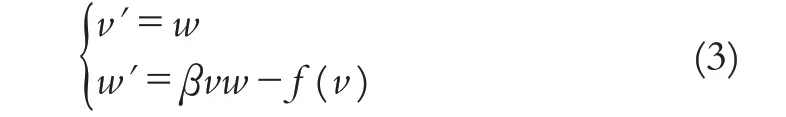
系统(3)的每一个解( v( x ),w( x ))对应着相平面v-w 上的一条轨线, 并在轨线上任意w ≠0 的点处斜率为

下面考虑非线性项f 为双稳态型情形, 即f ∈C1([ 0,+∞)) 且满足

2 平衡解分析

2.1 相图分析

对于f 是双稳态型情形, 系统(3)在v ≥0 半平面上有且只有3 个平衡点, 即点(0,0)、(θ,0)和(1,0).经计算可得(0,0)、(θ,0)和(1,0)所对应的特征值分别为:

这里只考虑0＜β ＜c0的情况, 其中c0是方程ut=uxx+f(u)唯一的行波解的波速[7].因为在这种情况下f"(0)＜0, f"(1)＜0, 所以对任意的β ∈(0,c0), (0,0)和(1,0)是鞍点.当时,(θ,0)是两向结点;当时, (θ,0) 是 单 向 结 点; 当β ＜时,(θ,0)是焦点.

先考虑方程(2)在v-w 相平面的第一象限中落到(1,0)的轨线Γ1.将它与方程

命 题1: 设β ∈(0,c0), 则 方 程(2)存 在 唯 一 解Ul∈C2([ 0,+∞)),满足下列条件

证明: 因为方程(2)满足条件(6)的解对应于v-w相平面中的轨线Γ1,分三步来讨论轨线Γ1的位置.

①先证: 存在ε ＞0, 使得当v ∈[1-ε,1)时, 轨线Γ1在轨线-Γ1的上方.

②再证: 当v ∈(0,1-ε)时, 轨线Γ1与轨线不能相交.

方程(5)等价于如下二维系统

假设轨线Γ1与轨线在(0,1-ε)内有交点, 记为(v0,w0).则由该假设以及第一步的证明结果可知

再利用方程(4)和方程(8)在点(v0,w0)处作比较可知, 当β ∈(0,c0)且v0∈(0,1-ε)时, 有这与(9)式矛盾.从而假设不成立, 即轨线Γ1与轨线在(0,1-ε)间不会相交.

③最后证:轨线Γ1不能经过点(0,0).

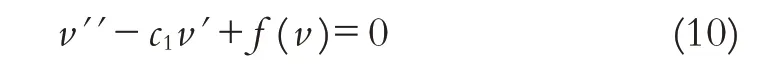
记方程(10)在v-w 相平面的第一象限中落到(1,0)的轨线为由于当且仅当c=c0时, 方程v""-cv"+f(v)=0 在相平面的第一象限内存在唯一的连接(0,0)和(1,0)的轨线再利用前两步的证明方法可知, 当v ∈[0,1)时, 轨线严格在轨线的上方,即轨线是第一象限内连接某正则点和(1,0)的轨线.再用同样的方法去比较轨线Γ1和轨线可知,轨线Γ1严格在轨线的上方,即轨线Γ1是第一象限内连接某正则点和(1,0)的轨线.

综上所述,命题1结论成立.

为了确定方程(2)的完整相图, 只需要再确定轨线Γ2与轨线Γ3的位置关系, 其中轨线Γ2是从点(0,0)出发, 经过第一象限的轨线; 轨线Γ3是从第四象限落到点(0,0)的轨线.其他轨线可由向量场方向以及在正则点处轨线不能相交这两个事实来确定.这里记轨线Γ2从点(0,0)出发经过第一象限后落到v轴 上 的 点 为轨 线Γ3从v 轴 上 的出发经过第四象限后落到点(0,0).

命题2:设β ∈(0,c0),则有

证明:记方程

将 轨 线Γ2与 轨 线作 比 较.任 取v0∈将方程(4)两边乘以w, 然后在(0,v0)上积分,得

即

即

用同样的方法比较轨线Γ3与轨线可得,在第四象限的公共范围上, 轨线Γ3严格在轨线的上方,故

综上可知,命题2的结论成立.

由命题1、命题2 及平衡点分析等, 可以画出方程(2) 在β ∈(0,c0) 情 形 时 完 整 的 相 图.当时,(θ,0)是焦点, 此时的相图如图1 所示; 当时,(θ,0)是结点,此时的相图如图2所示.

图1 取非线性项f(u) = 8u(1- u)(u - 1/3)时方程(2)对应的相图Fig.1 Phase diagram corresponding to the equation (2)with nonlinearity f(u) = 8u(1- u)(u - 1/3)

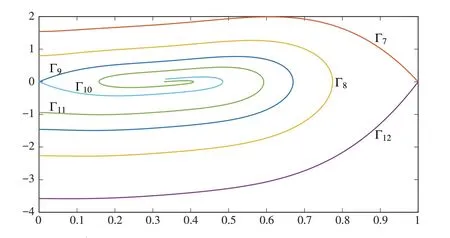
图2 取非线性项f(u)=8u(1-u)(u-1/3)[81(u-1/3)2+1/9]时方程(2)对应的相图Fig.2 Phase diagram corresponding to the equation (2)with nonlinearity f(u)=8u(1-u)(u-1/3)[81(u-1/3)2+1/9]

2.2 分类结果

则当β ∈(0,c0)时, 方程(1)的所有非负有界解有如下几类:

3 结语

本文研究了双稳情形下β∈(0,c0)时方程(1)各个非负有界平衡解,在这个过程中借助轨线和的轨线的特性，经过一系列分析后得到方程(2)各个轨线的位置关系, 进而画出完整的相图并进行平衡解分析.

而当β ∈[c0,∞)时,根据现有轨线的性质不易构造适合方程(2)的上下解并分析出它的轨线位置, 所以这个问题依然需要进行进一步的探索研究.