级数求和中的裂项法研究

薛利敏，田亚丽

(1.渭南师范学院数理学院，陕西 渭南714099;2.渭南高新中学，陕西渭南714000)

无穷级数是微积分学的一个重要组成部分，它是表示函数、研究函数性质以及进行数值计算最有力的工具，在实际问题和理论研究中有着广泛应用。［1］无穷级数就是对数列u1，u2，…，un，…进行无限求和的前n项部分和(Sn=u1+u2+…+un)数列收敛，S叫作这个级数的和。文献［2－5］等大部分教材都把级数用定义求和当作例子，因为这个级数的前n项部分和数列 Sn{ }可以用裂项相消法求出其表达式。然而，能用定义求其和的级数非常少，原因是不容易求出级数的前n项部分和数的具体表达式。本文采用裂项相消法求一些级数的和，首先给出部分一般性的级数求和公式，然后，利用这些公式求出更多级数的和。在证明这些级数求和公式时，要用到一个简单的结论:设等差数列

1 主要结果

1.1 裂项相消法求级数的和

定理1设等差数列 { an}的公差d≠0，则级数

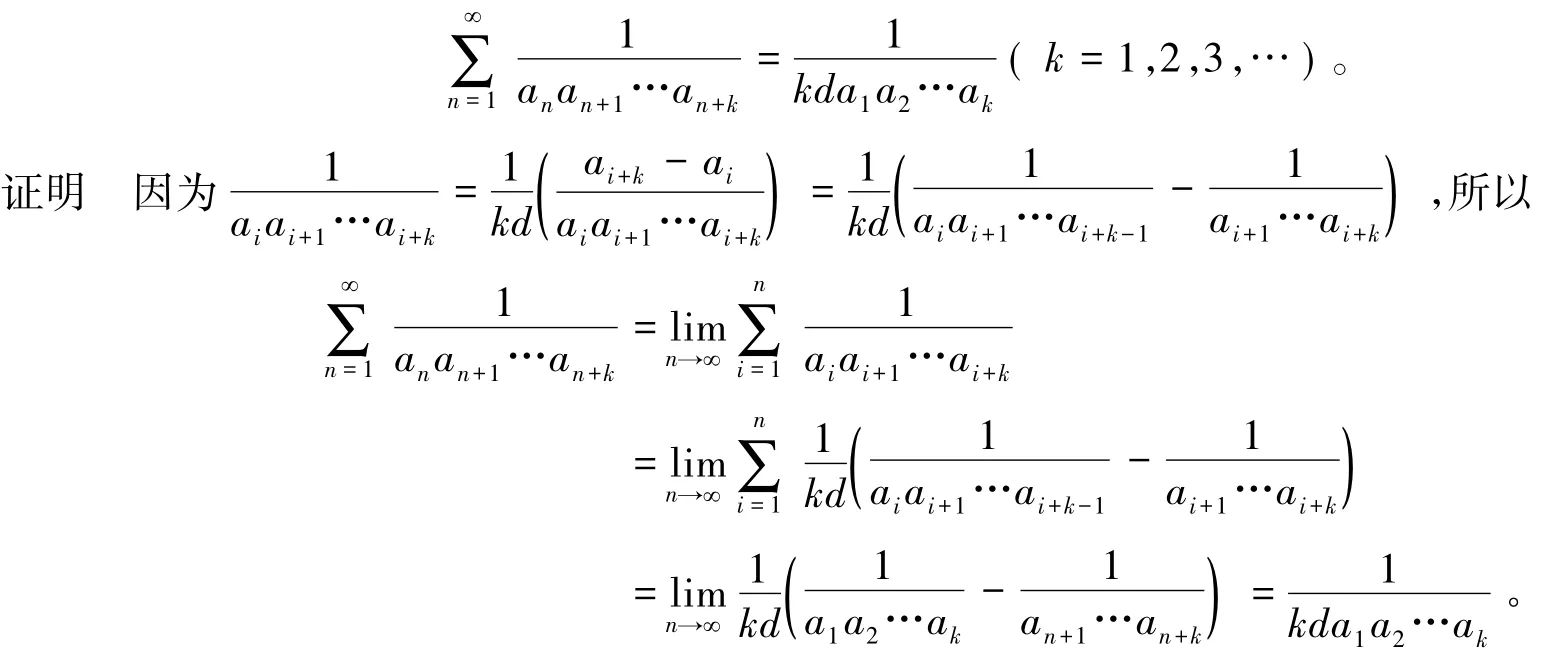
根据定理1，我们容易得到下面级数的求和公式。

在定理2中，特别地，当等差数列 an{ }= n{}时，则有下面级数的求和公式。

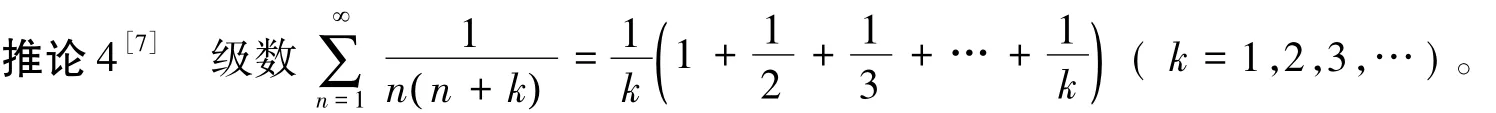
在推论1中，分别取k=1、k=2和k=3，我们容易得到下面级数的求和公式。

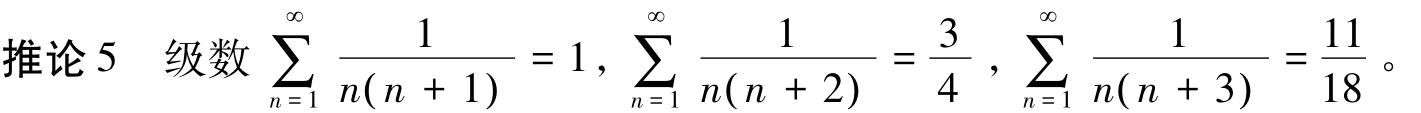
设数列 { an}为等差数列，数列 { bn}为等比数列，不妨称级数为差比型级数，对于差比型级数可以通过裂项相消法求出其前n项部分和数列 { Sn}通项的具体表达式，进而求出差比型级数的和。

1.2 裂项公式法求级数的和

2 应用举例

3 结语

根据上面的讨论，我们通过裂项法得到了4个定理和5个推论，进一步得出了2个重要结论:(1)形如(其中:.P1(n)是n的1次多项式的级数能求和;(2)形如Pm(n)是n的m次多项式)的级数能求和。根据这些公式和结论以及裂项法，我们还可以求出其他级数的和。