A Model Analysiswhich Consider Direct cell-to-cell Transmission of HIV

姬文娟 李 斌 罗 欣

（西安卫星测控中心，陕西 渭南714000）

0 Introduction

HIV-1 can spread within an infected host by two mechanisms:(a)release of cell-free virus particles and (b)direct passage between infected and uninfected cell.Actually in cell culture we discover that direct cellto-cell transfer is more rapid and efficient than cell-free spread,and cellto-cell passage may help viruses evade elements of the immune response.In cell-to-cell transmission of HIV-1 reverse transcription is a crucial event.However,a potent reverse transcriptase (RT)inhibitor which completely blocks virus production-following infection with cell-free virus,dose not inhibit cell-to-cell transmission of HIV-1 from virusinfected cells to uninfected target cells[1].

In the previous models the authors only dealt with infection of cells by free virus,but in HIV and the pathogenesis of AIDS of Jay A.Levy[2],who implies direct cell-to-cell transmission of virus has been reported in some research,and even this type of infection is more important.So We decide to consider this aspect into above the model.Such as:(1)s represents the rate at which new T cells are created from sources within the body.T cells can also be created by proliferation of existing T cells,in which p is the maximum proliferation rate and is the T cells population density at which proliferation shuts off.Here the rate of death per cell is a constant for uninfected cells T andδfor uninfected cells,c is the death rate per virus particle.In which the rate of infection is given by,with being the infection rate constant.N represents the total number of virus particles produced by an infected cell during its lifetime.In the presence of RT inhibitors,where is the effectiveness of the RT inhibitors.represents the infection rate between T and.

1 Main results

The basic reproduction number for system(1)is defined the expected number of secondary individuals produced by an individual in its lifetime in a completely susceptible population (which means).We can obtain by calculation.Clearly,we can denote.

Theorem1.1.If the only disease-free equilibrium is locally asymptotically stable.

Theorem1.2.If the disease-free equilibrium is unstable,and the endemic equilibrium is locally asymptotically stable.We mark,where f is a smooth function.If for T,and denote,is globally asymptotically stable.

2 Proofs

2.1 Boundedness and stability of the disease-free state

Lemma 2.1.1.Solutions of system(1)are nonnegative and bounded.Proof.From system(1)we can obtain the positive quadrant is positively invariant,so the solutions are nonnegative,which accords with biological significances.Then since for.let according to the first two equations of system(1).Let A＞0,and ensure that.

Lemma 2.1.2.If the disease-free equilibrium of system(1)is locally asymptotically stable.

Proof.The Jacobian matrix of system(1)at is

Clearly,<0.

Finally the trace of is negative.The result follows immediately.

Lemma 2.1.3.If the disease-free equilibrium of system(1)is globally asymptotically stable.

Proof.First we consider the disease-free equilibrium is globally attractive.From the first formula of system (1)we known,denote.Clearly,it is easy to say.In other words.From the second and third formula we have.Assume such a system:Clearly,is positive invariant set of system(3).Thus is the maximum invariant set of system(2).According to LaSalle invariant principle.Then according to comparison principle,we can obtain.So the disease-free equilibrium is globally attractive.Then from Lemma 2.1.2.he disease-free equilibrium of system (1)is globally asymptotically stable.The result follows simply.

2.2 Stability of the disease steady state.

Lemma 2.2.1.If the endemic equilibrium is locally asymptotically stable.

Proof.The Jacobian matrix of system(1)at is,

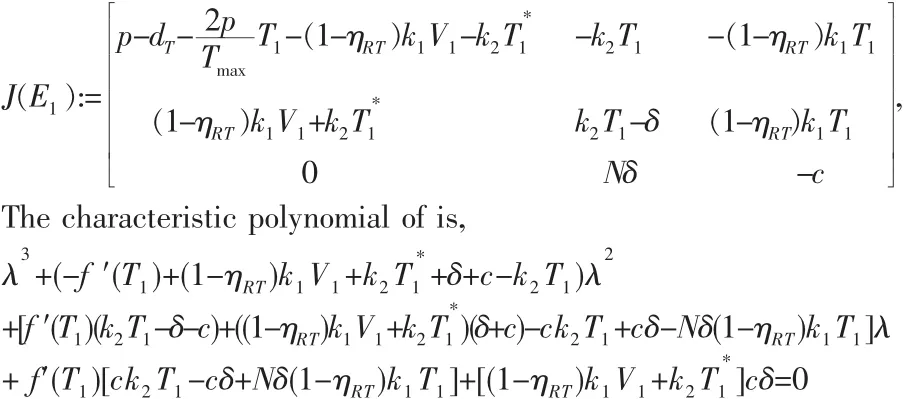
From Routh-Hurwitz criterion,clearly we can obtain,can be expanded:

Next we consider whether.After is combined a number of terms,all terms are positive except such a term including,which can be settled＞0.According to Routh-Hurwitz criterion,the eigenvalues of are all negative.The result follows immediately.The endemic equilibrium is locally asymptotically stable.

Lemma 2.2.2.If the endemic equilibrium is globally asymptotically stable.

Proof.we prove the global stability of by using such a approach which constructs Lyapunov function and makes use of LaSalle invariant principle.According to Lemma 2.1.1.the unique positiveequilibrium is in the set.We shall prove the global stability of in the interior of D.

Define Lyapunov function.By the relationship of arithmetic and the geometric means,it follows that,and if and only if and.We need to have when we form.

It is obvious that the maximum invariant set of(1)on the set is the singleton set.Therefore,it follows by the LaSalle Invariable Principle that is globally stable in the set D.

［1］Jay A.Levy.HIV and the pathogenesis of AIDS,2010[Z].

［2］Liao Xiaoxin.Mathematical Theory and Application of Stability,1988[Z].

［3］Michael Y.Li and James S.Muldowney,Global Stability for the SEIR Model in Epidemiology,1994[Z].