基于非凸稀疏模型的优化算法在金融投资组合中的应用

李 蒙

(渭南师范学院网络安全与信息化学院，陕西渭南714099)

1 Markowitz投资组合理论

1.1 Markowitz投资组合理论及其现状

1952年，Markowitz提出的投资组合理论［1］奠定了现代金融学的基础，该理论认为分散投资、进行投资资产的多样化可以有效降低市场的非系统风险。该理论包含两个重要内容:均值—方差分析方法和投资组合有效边界理论。Markowitz经过大量观察和分析得出:假定在相同回报率的两个资产之间进行选择的话，理性投资者都会选择风险小的资产。这也表明投资者在追求高回报的同时要承担高风险。因此，出于回避风险的考虑，投资者一般会持有多样化的投资组合。Markowitz从对收益和风险的定量分析出发，系统地研究了投资组合的特性，从数学上解释了投资者规避风险的行为，并提出了投资组合优化方法。

实际上，人们进行投资，是在不确定性的收益和风险之间选择博弈。投资组合理论用均值—方差来刻画这两个关键因素。所谓均值，指投资组合的期望收益率，它是单只证券的期望收益率的加权平均，权重为对应的投资比例。所谓方差，指投资组合的收益率的方差。我们把收益率的标准差称为波动率，它刻画了投资组合的风险。

投资组合理论研究的核心问题是确定人们在投资决策中如何权衡收益和风险。如果将一个投资组合在一个以波动率为横坐标、收益率为纵坐标的二维平面中描绘出来，将形成一个点。而对于所有的有效投资组合，在上述坐标平面中将形成一条连续的凹曲线，称之为投资组合的有效边缘。投资组合的有效边缘一经确定，就可以在这条有效边缘上确定效用最大的投资组合了。在波动率—收益率二维平面上，任意一个投资组合要么落在有效边缘上，要么落在有效边缘下。因此，有效边缘包含了全部最优投资组合，理性投资者只需在有效边缘上选择投资组合。

Markowitz提出投资组合理论后，产生了诸多的投资组合新发展:多期的投资组合，在不同风险测度下的投资组合，基于交易费用和流动性的投资组合，基于非效用最大化的投资组合理论等等。在投资组合理论的发展历史中，以Sharpe的工作最为突出，其于1964年发表论文开辟了投资组合的另一途径，通过引入描述证券收益的单因子模型从而大大简化了Markowitz理论的模式，为实际投资过程中成功运用Markowitz理论提供了便利。然而该理论并不完善，随后Cox、Ingersoll和Ross等人提出了多因子模型，我们称之为套利定价模型。Fama于1965年从理论和经验两方面出发，利用统计学方法对资本市场证券价格作了深入研究，提出了有效市场理论。随后的投资组合发展均是以上述一些理论为基础。在我国对投资组合的研究最早可以追溯到20世纪90年代，当然也涌现出很多有价值的文献。

1.2 Markowitz模型解释

投资组合理论研究的是在最大化预期收益和最小化投资风险的前提下如何分配一个投资者的可用资产到预设的资产集中。我们用n表示可用资产的数目，用μ表示资产的预期收益向量，Q是一个对称半正定矩阵，Q中的元素qij表示资产i和j的收益方差。通常情况下，向量μ和矩阵Q都是不知道的，但是可以通过历史数据估计出来。

假定每一份资产都是可用的，而且可以进行完全投资。令向量x∈Rn为决策变量，x中的每一个元xi是向资产i的投资份额，i=1，2，···，n。因为可用资本可以完全用来投资，而且不允许卖空，向量x满足约束条件eTx=1，x≥0。其中e是一个全1的列向量，μTx度量投资的预期收益，xTQx度量投资风险。经典的Markowitz投资组合模型是需要同时考虑两个目标:收益最大化和风险最小化。

经典的Markowitz投资组合模型中，这个双目标问题可以转化为一个单目标优化问题，即在预期收益给定的条件下，最小化投资风险。一般的，这个优化问题可以描述为凸二次规划问题:

这是一个凸二次规划问题。

给定参数β的值，β是投资的预期收益，问题(1)具有唯一的最优解:

上述凸二次规划模型主要的问题在于:资产的均值和协方差是通过历史数据估计得来的，不具备充分的准确性。事实上，收益的均值是很难进行估计的，这种现象被称为均值模糊。此外，均值方差模型对输入参数的分布非常敏感，这样会放大估计误差，导致极限投资，样本外测试结果差。后来又提出了一些改进的Markowitz模型，得到稳健的投资。在文献Combining invest views with market equilibrium中均值和方差的估计用的是贝叶斯估计。后来，为了使投资的优化进程更加多样化，模型中又加入了额外的投资约束，针对最小化风险的投资分配，提出了James－Steiner估计，接着又有了稳健估计。为了降低交易费用，减少投资管理的复杂程度，提出了一类重要的投资组合问题，这类问题通过限制资本的投资数量来实现这一目的。加入这一约束，模型转化为求解稀疏的投资组合问题，补救了传统的投资组合模型的高度不稳定性。

特别地，通过对问题(1)加入控制资产数目的约束条件对Markowitz模型进行修改。这类问题被称为基数约束的投资组合问题:

其中:‖x‖0是x的零范数，表示向量x中的非零元的个数;参数K是投资项目个数的上限。

总之，现代投资组合问题主要包含以下3个目标函数:

(1)最小化投资风险xTQx，即min xTQx;

(2)最大化投资预期收益μTx，即max μTx;

(3)最小化所选投资项目数 ‖x‖0，即min‖x‖0。

上述基数约束的投资组合问题(3)中对于投资项目数量的限制可以转化为将参数K控制为一个充分小的值，即得到本文主要研究稀疏投资组合问题的数学模型:

其中:μ为各资产收益率，Q为各资产方差协方差矩阵，α为投资者可接受风险上限，β为投资者期望收益率。事实上，这是一个NP－hard问题。

2 罚函数分解法

本文主要考虑稀疏近似问题，一般的l0最小化问题都伴随着l0范数是目标函数或约束条件的一部分。2013年，Lu等［2］针对这一问题提出罚函数分解法(Penalty Decomposition)，该算法可以有效求解此类问题。

首先给出这类问题的一阶最优性条件，然后介绍解决这类问题的罚函数分解算法，即将原问题转化为一系列罚函数子问题，通过分块协同下降法求解罚函数子问题，从而得到原问题的解。理论证明，在合理的假设下，通过罚函数分解法所得序列的收敛点满足一阶最优性条件。此外，原问题中l0是惟一的非凸项，经证明该收敛点是局部极小点且可以证明通过分块协同下降法产生的序列的收敛点是罚函数子问题的鞍点。因为l0是唯一的非凸项，所以该收敛点是罚函数子问题的局部极小点。

现如今，稀疏问题应用十分广泛。例如，在压缩传感中，大的稀疏信号可以通过相对小数量的线性度量进行编码，可将问题转化为求解一组线性等式组或线性不等式组。相似的方法已经广泛地应用于线性回归领域。近年来，稀疏逆协方差选择成为发现图像模型中条件独立项的重要工具。目前比较主流的方法是在最大化对数似然函数的同时，寻找近似的稀疏逆协方差矩阵。同样，聚类问题中处理特征选取问题时提出了一个很有前景的稀疏Logistic回归方法，即在最小化平均Logistic损失的同时寻求稀疏解。转化为数学的方法，以上所有的应用都可以表述为下面的l0最小化问题:

其中:r＞0，υ＞0，通过调整r、υ的大小来控制问题的稀疏程度，X是n维欧氏空间Rn的闭凸集，f:Rn→R，g:Rn→Rm，h:Rn→Rp都是连续可导函数，‖xJ‖0指x中被指标集J标注的子向量的基数。针对这类问题的特殊情况提出了一些算法。例如，迭代阈值方法和匹配追踪方法都是为了解决压缩传感中出现的l0正则化最小二乘问题发展起来的，但是它们不能用来处理一般的l0最小化问题(5)和(6)。处理问题(5)和(6)的一个流行的方法是用l1－norm‖·‖1替换 ‖·‖0，然后求解这个松弛问题。在诸如压缩传感应用方面，在一些合理的假设下，这个方法可以用来求解问题(5)和(6)。近年来，又提出了另外一些松弛方法，即用lp替换l0。一般地，对于这些方法的解的性质不是很明确。2014年，Lu［3］针对带上下界约束的L0正则化问题

提出Hard阈值算法如下:

本文中我们用罚分解方法求解问题(5)和(6)，即通过分块协同下降法求解一系列罚函数子问题。在一些合理的假设下，通过罚分解方法产生的序列的收敛点满足问题(5)和(6)一阶最优性条件。另外，当h是仿射函数，f和g是凸函数时，该收敛点是问题(5)和(6)的局部最小点。同时证明了通过分块协同下降法产生的序列的极限点是罚函数子问题的鞍点。另外，当h是仿射函数，f和g是凸函数时，该收敛点是罚函数子问题的局部最小点。

2.1 问题(5)的罚函数分解法

经分析，问题(5)可以等价的表述为:

与之相关的二次罚函数定义如下:

其中:罚参数ρ＞0。

现在提出解决问题(9)的罚函数分解法，可以等价的处理问题(5)。每一个罚函数子问题通过分块协同下降法近似地解决。

(1)令l=0，通过步骤(a)(b)(c)(d)应用分块协同下降法求解罚函数子问题

的近似解。

转向(2)，

(d)令 l← l+1，转向(a);

(2)令 ρk+1:= σρk;

(4)令 k←k+1，转向(1)。

2.2 问题(6)的罚函数分解法

经分析，问题(6)可以等价的表述为:

与之相关的二次罚函数定义如下:

其中:罚参数ρ＞0。

现在提出解决问题(15)的罚函数分解法，可以等价的处理问题(6)。每一个罚函数子问题通过分块协同下降法近似地解决。

令 εk{ }为正项递减序列，对于给定的ρ0＞0，σ＞1，q0定义如(11)。选取任意的∈Y，常数γ满

(1)令l=0，通过步骤(a)(b)(c)(d)描述的分块协同下降法求解罚函数子问题

3 数值实验及算法比较

这一部分主要是通过数值实验测试我们前面介绍的罚函数分解法，将其应用于稀疏投资组合模型(4)中，并将结果与遗传算法运行结果相比较。

选取沪深300指数中的10个成分股(苏宁电器、上港集团、宝钢股份、中国石化、中信证券、招商银行、中国联通、上海汽车、贵州茅台、中国平安)从2009年1月5日至2009年6月4日100个交易日的收盘价(单位:元)，数据来源于新浪财经数据中心。分别通过罚函数分解法和遗传算法计算投资者在这10个成分股中的最优资产配置比例。

3.1 罚函数分解法

目标函数

与之相关的二次罚函数定义如下:

其中:罚参数ρ＞0。

运用罚函数分解法求解结果为:x=［0 0 0 0 0 0 0 0.6732 0.3268 0］。

结果解释:将用于投资总资产的67%买入上海汽车股票，33%买入贵州茅台股票。

3.2 遗传算法

遗传算法(Genetic Algorithm，GA)［4］是借鉴生物界自然选择和群体进化机制形成的一种全局寻优算法。应用遗传算法求解优化问题［5］时，首先将解空间的设计变量转换为遗传算法中的基因型数据结构，形成遗传算法中的染色体;然后通过选择、重组、变异模拟生物在自然界中的遗传过程，得到新一代群体;不断迭代，直到新一代群体满足要求，即可得到问题的解。将遗传算法应用于稀疏投资组合模型(4)中，在与上述实验同样的数据下，计算投资者的最优资产配置比例。

运用遗传算法工具箱［6］进行求解，参数设定如图1所示，结果为:

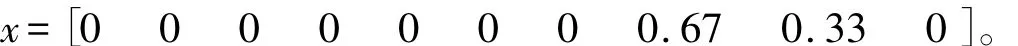
图1 遗传算法工具箱求解界面

遗传算法的收敛解与罚函数分解法得到的结果一致，因此，罚函数分解法可以用来处理投资组合问题，且效果较好。

4 结论

稀疏问题已经遍布各个领域，比如投资组合、指数追踪、压缩传感、医学光源重建等，而对于稀疏问题的求解一直是NP难问题。因此，罚函数分解算法的提出有效地解决了这一问题，该算法对不同领域的稀疏问题有广泛的适用性，同时算法的收敛性保证了求解结果的有效参考价值。