InAs/GaSb量子阱中太赫兹光电导特性∗

魏相飞 何锐 张刚 刘向远

(皖西学院电气与光电工程学院,六安 237012)

1 引 言

太赫兹技术由于具有信噪比高、相应快等优点和广泛的应用价值成为世界各国研究机构关注的焦点,是本世纪重大新兴科学技术领域之一[1,2].太赫兹半导体器件由于体积小、易集成和成本低等优点,在太赫兹成像、通信、医学、无损检测和安检等应用系统中将发挥了巨大作用[3,4].在传统的半导体量子阱中,导带和价带间的带隙比较大,因此带间跃迁所需要的光子能量比子带间跃迁所需要的光子能量大得多,使其在太赫兹器件的应用中受到限制.与此形成显著对比的是在基于InAs/GaSb的二类、断带半导体量子阱中,GaSb层的价带顶比InAs层的导带底高,因此GaSb价带中的电子会转移到InAs的导带上.于是在InAs层形成二维电子气,而在GaSb层中会形成二维空穴气,并且二维电子气和二维空穴气在空间上是分离的,电子和空穴的能带有交叠,这使得该量子阱系统有望在太赫兹器件中取得重要应用.基于InAs/GaSb的二类量子阱结构自1983年由Altarelli理论提出[5],并于1987年首次在实验上制备成功之后[6],由于其独特的能带结构引起了人们极大的研究兴趣.更重要的是该量子阱系统具有响应波段宽且精确可控、工作温度高、载流子寿命长、暗电流低和均匀性好等优点,使其在长波、多色以及非制冷红外焦平面阵列等方面具有广阔的应用前景,成为第三代红外探测器技术的最佳选择[7].对InAs/GaSb异质结的双色远红外光吸收谱的理论研究已经证明,此系统可以作为室温下工作的双色远红外探测器[8],有力地支持了Norton等关于用该系统做第三代红外探测器的实验发现[9−12].近年来,Liu等发现InAs/GaSb量子阱系统是一种良好的拓扑绝缘体材料[13],Knez等对该量子阱系统进行了系统的实验研究,相继在该系统中发现了螺旋边缘模式(helical edge modes)和Andreev反射等拓扑现象[14−18],进一步证明了InAs/GaSb基的量子阱系统和HgTe/CdTe量子阱一样,是一种量子自旋霍尔绝缘体.

目前对基于InAs/GaSb的II类量子阱及超晶格系统的研究仍然局限在红外探测器方面,考虑到该量子阱系统中载流子的能谱可以通过量子阱的结构进行调控,因此其光电性质方便可调,这也使得该半导体量子阱材料比石墨烯等其他材料在光电器件方面更具有优势[19,20].基于此,本文系统地研究了基于InAs/GaSb的II类量子阱系统中光电导对量子阱结构的依赖关系,考虑温度对光电导的影响,探索该量子阱系统在室温太赫兹器件方面的应用.

2 理论方法

本文用半经典的玻尔兹曼方程方法研究AlSb/InAs/GaSb/AlSb半导体量子阱系统在沿着生长方向线性极化光场作用下的光电性质.在外加电磁场下,体系的哈密顿量可以写为

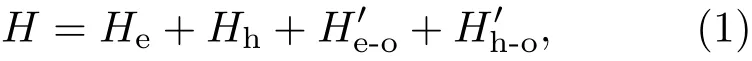
式中,分别是电子和空穴的单粒子哈密顿量,在计算中我们将势能的零点取在InAs层的导带底,其中,=e,h,分别表示电子和空穴的动量,是载流子的有效质量,Ui(zi)是载流子所受到的限制势;为电子或空穴与光子相互作用的哈密顿量,其中,“±”分别表示电子和空穴与沿着生长方向线性极化的光场的相互作用.在本文中,我们用传递矩阵方法求解量子阱沿着生长方向的能级和波函数[21−23],则电子和空穴的波函数及能谱为其中,是电子或空穴沿着生长方向的波函数,k为二维波矢,为电子或空穴的能级.

本文考虑只有最低的电子带和最高的空穴带分别被电子和重空穴所占据的情况,即基态被占据的情况.电子或空穴从i层跃迁到j层时,时间依赖的玻尔兹曼方程可以写为

其中,(k,t)是电子或者空穴的动量分布函数,gs=2为自旋简并指标.在方程(2)中对应于电子或空穴在带间的跃迁即载流子在不同材料层之间的跃迁;而对应于电子或空穴的带内跃迁即载流子在同一材料层中的跃迁.跃迁概率可以由费米黄金规则给出,

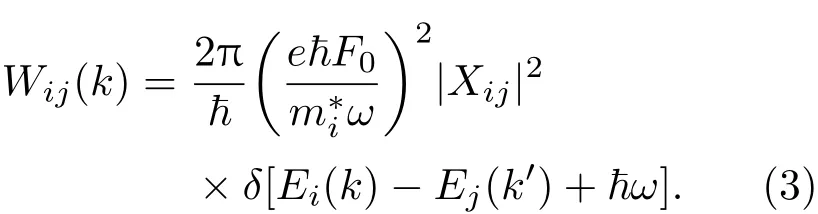
由于散射概率Wij(k)的复杂形式,玻尔兹曼方程(2)没有简单的解析解,本文用平衡方程方法求解玻尔兹曼方程,研究该量子阱系统中的光电导性质[24].在方程(2)的两边同时乘以得到质量平衡方程:

从方程(4)左边的第二项可以看出,同一带内的跃迁相互抵消,即不引起电子数的变化,只有带间跃迁才改变电子数或空穴数,从而对光电导有贡献.并且利用电子浓度和分布函数的关系:

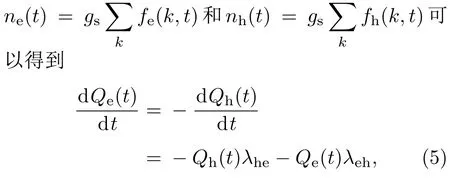
式中,分别是电子和空穴的电量,满足其中,S为量子阱受光面积.从方程(5)可以得到总电荷守恒条件:

定义λE和λC分别为电子的发射率和俘获率,并且用电子和空穴的稳态能量分布函数分别代替其与时间相关的动量分布函数,即其中fi(E)是电子或空穴的费米狄拉克分布函数.则电子的发射率和俘获率可以写为

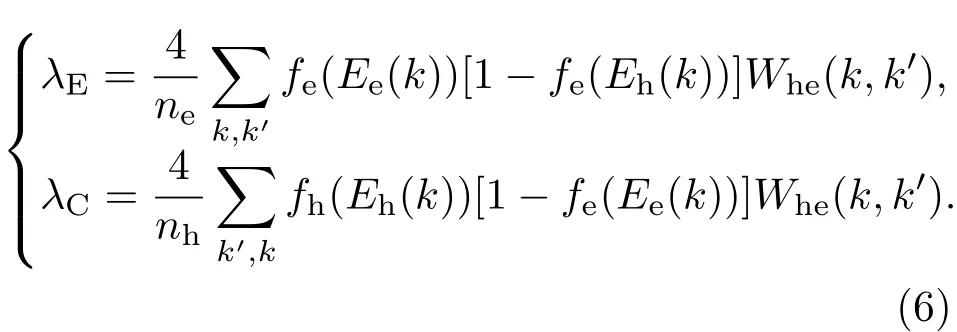
根据电流的定义:I=dQ/dt,由方程(5)得

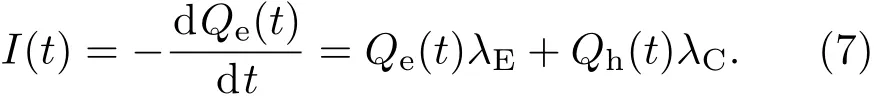
在频率为ω的电磁场δVt=V0eiωt的驱动下,量子阱中电子的电量Qe(t)是运动的电量δQe(t)和被激发的电量之差:

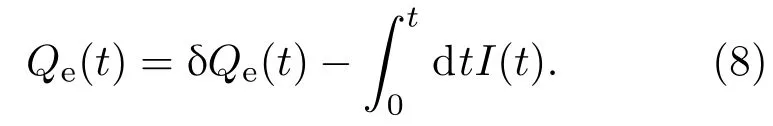
当外加辐射场比较弱时,电荷和驱动场为线性响应:

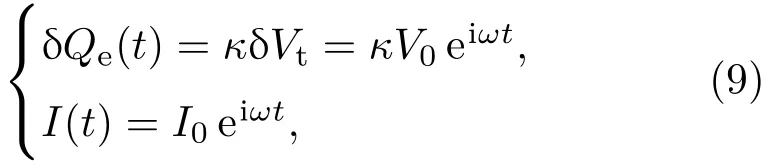
其中电荷和电压的比例系数为

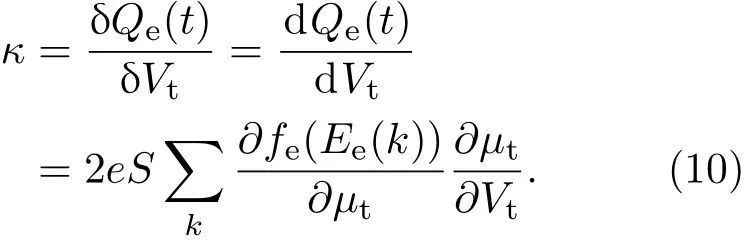
在电磁场比较弱时,电磁场只影响体系的费米面,在线性响应下,则

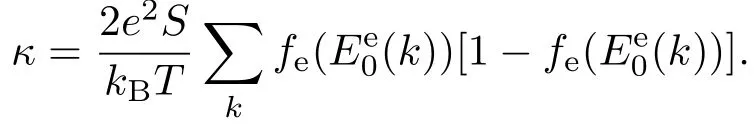
这个结果表明电子或空穴的发射或者俘获主要通过费米面附近的载流子的跃迁发生,因为费米面附近的电子或空穴更容易被激发.由此得到回路中的电流为

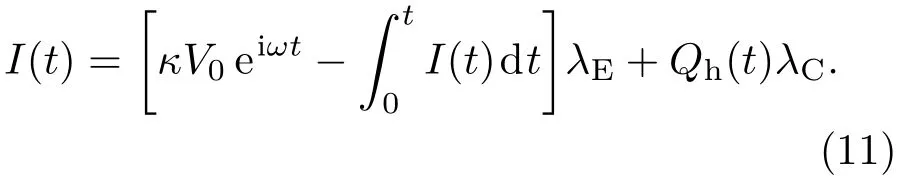
方程(11)两边同时对时间t求导得到

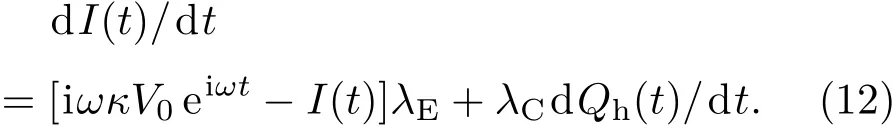
在平衡条件下总的电荷数守恒,即电子和空穴电荷的变化量应该相等.在该量子阱中电子数和空穴数的增减情况一致,则dQh(t)/dt=−dQe(t)/dt=I(t),在此条件下,方程(12)有解析解.利用电导的定义:G=I0/V0得到

利用费米狄拉克分布函数作为电子和空穴的能量分布函数可以求得电子的发射率和俘获率的解析解:

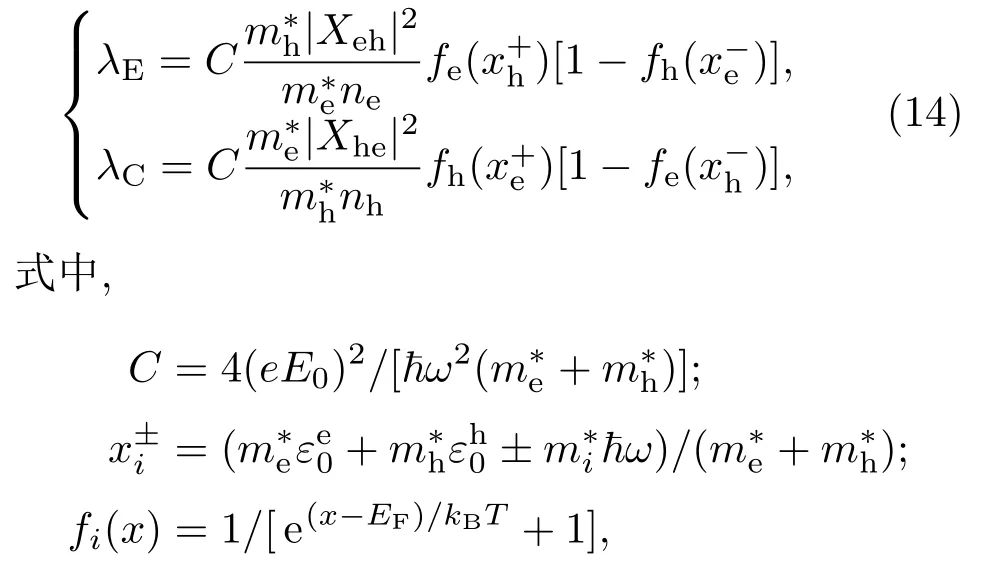
其中,EF是体系的费米面.

3 数值结果和讨论

本文用半经典的玻尔兹曼方程方法研究了基于InAs/GaSb的二类、断带半导体量子阱结构对光电导的影响.根据已知的样品参数,如电子和空穴的有效质量、量子阱的限制势能、介电常数和样品厚度等,用传递矩阵方法求解了量子阱中电子和空穴的能级和波函数.在计算中我们选取的样品参数为为电子的裸质量.图1给出了InAs和GaSb的厚度LInAs=LGaSb=8 nm时,电子和空穴的波函数.从图1可以看出,电子和空穴分别被限制在InAs层和GaSb层,在InAs和GaSb的界面(z=13 nm)处,电子和空穴的波函数有交叠,这种交叠对电子和空穴在两层间跃迁起着重要作用,而且电子波函数向空穴层的隧穿更加明显,这主要是因为电子的有效质量更小,更容易发生隧穿.本文只考虑电子和空穴的基态,即只有最低的电子态和最高的空穴态分别被电子和空穴占据的情况.表1列出了不同量子阱厚度下电子和空穴的能级和载流子浓度,其中费米能级取为126 meV,作为计算中惟一的输入参数.

表1 不同量子阱结构中电子和空穴的能级和载流子浓度Table 1.The subband energies and densities for carriers at different structures of the QWs.

图1 InAs和GaSb的厚度均为8 nm时,电子和空穴的波函数(实线为电子的波函数,虚线为空穴的波函数,电子和空穴的波函数在界面z=13 nm处有较强的耦合),内插图为AlSb/InAs/GaSb/AlSb量子阱结构示意图(其中实线为量子阱的导带,虚线为量子阱的价带)Fig.1.The wavefunctions for electrons and holes with LInAs=LGaSb=8 nm(The solid line and dashed line represent the wavefunctions for electron and hole,respectively.The wavefunctions for electron and hole overlap at the interface z=13 nm),and the inset shows the scheme of the structure of the AlSb/InAs/GaSb/AlSb quantum wells where the sold line and dashed line represent the conductance and valence band,respectively.

本研究发现,当在基于InAs/GaSb的二类、断带半导体量子阱中加上线性极化的电磁场时,载流子会发生光跃迁,其物理过程是电子或空穴吸收光子获得一定的能量,从量子阱的一层转移到另一层从而使体系具有光电导,从能级情况来看就是电子或空穴吸收光子跃迁到能量更高的态,所以光吸收伴随着载流子的跃迁.这个过程对应于电子-空穴对的产生和复合,因此也对应于电荷在量子阱中的转移.在辐射场的作用下,量子阱中既有电子-空穴对的形成,也有电子-空穴对的湮灭.而对应于前一种情况,不同层中的电荷数会增加;而对于后一种过程,不同层中的电荷数会减少.在InAs/GaSb的二类、断带半导体量子阱中,电子和空穴分别在两种不同的材料层中,电子-空穴对的形成和湮灭对应于电子和空穴在两层间的转移,因此可以形成层间的电流.图2给出了温度为4.2 K时,量子阱中由于电子跃迁产生的光电导,插图为由于空穴跃迁引起的光电导.从图2可以看到光电导在太赫兹(0.2 THz)频率范围出现了非常强的吸收峰,这表明当辐射场的频率在太赫兹区时,器件中可以观测到非常强的光电导信号,因此可以用太赫兹频率的电磁场在器件中激发光电流.图2内插图是空穴从GaSb材料层向InAs材料层跃迁形成的光电导.从图2可以看出,电子跃迁形成的光电导比空穴跃迁形成的光电导信号强得多,这主要是由于空穴的有效质量更大,难以跃迁,所以一般情况下,在基于InAs/GaSb的二类、断带半导体量子阱中光电导主要是由于电子从InAs层向GaSb层的跃迁所引起的.

图2 InAs和GaSb的厚度均为8 nm,温度为4.2 K时电子跃迁所引起的光电导Ge/G0,插图为由于空穴跃迁所引起的光电导Gh/G0,其中G0=e2/~Fig.2. The photoconductivity Ge/G0induced by the electron transitions at T=4.2 K with LInAs=LGaSb=8 nm.The inset shows the photoconductivity Gh/G0induced by the hole transitions with G0=e2/~.

图3给出了T=4.2 K时不同量子阱结构中的光电导.实线为InAs和GaSb层的厚度均为8 nm时的光电导,虚线和点线分别为LInAs=15 nm,LGaSb=8 nm和LInAs=8 nm,LGaSb=15 nm时的光电导.从图3可以看出,当InAs和GaSb层的厚度均为8 nm时,光电导的峰值约为0.2 THz.随着InAs层厚度的增加(LInAs=15 nm,LGaSb=8 nm),光电导的强度有所下降且峰值位置发生红移现象.当InAs和GaSb层的厚度分别为8和15 nm时,虽然光电导峰的强度很大,但其峰值落在了0.02 THz附近,红移现象更加明显.这主要是因为当LInAs=8 nm,LGaSb=15 nm时,空穴的浓度比较大(表1),所以在该量子阱结构中由空穴在费米面附近的跃迁对光电导的贡献起主要作用.由此可见,量子阱的结构对其光电导特性有着非常重要的影响,因为量子阱结构不仅能够影响量子阱中载流子的浓度和能级,还对其波函数的耦合有重要影响.当InAs和GaSb层的厚度均为8 nm时,电子和空穴波函数的耦合比较大(图1),因此载流子在不同材料层中跃迁的概率更大.在基于InAs/GaSb的二类、断带半导体量子阱中的光电导由载流子的浓度、能级、波函数的耦合以及载流子的占据情况决定,而这些物理量都与量子阱的结构有着重要的关系,因此可以通过量子阱结构的优化,对其光电性质进行调节,设计性能优化的光电器件.

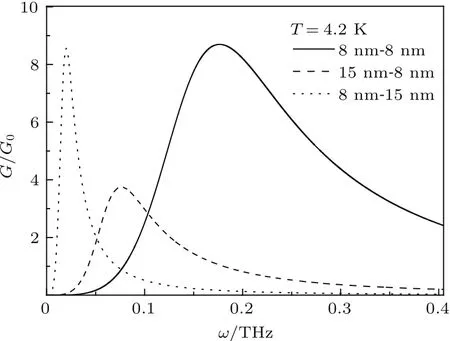
图3 T=4.2 K时不同量子阱结构中的光电导(实线为InAs和GaSb的厚度均为8 nm时的光电导,虚线和点线分别为LInAs=15 nm,LGaSb=8 nm和LInAs=8 nm,LGaSb=15 nm时的光电导)Fig.3. The conductivity at different structures of the quantum wells with T=4.2 K(The solid line,dashed line and dotted line represent the conductivity at LInAs=LGaSb=8 nm,LInAs=15 nm,LGaSb=8 nm and LInAs=8 nm,LGaSb=15 nm,respectively).

载流子在不同材料层之间的光跃迁强烈地依赖于体系中载流子的占据情况,而其分布函数与温度有关,所以温度对光电导有非常大的影响.图4给出了在不同温度下光电导随着辐射场频率的变化关系,量子阱的厚度取为LInAs=8 nm,LGaSb=8 nm.随着温度的升高,光电导的峰值变小并且峰的位置向能量低的方向移动即红移.从光电导的表达式(13)可以看出光电导的峰值的位置与电子的激发率和俘获率有关,即当电子激发率和俘获率之和与光子频率相等时,光电导取得最大值,其频率对应的位置在ω∼λE+λC.对温度的影响还反映在光电导表达式中电子的激发率λE和俘获率λC上,这些量都是与温度有关的物理量.随着温度的降低,费米面以下的电子的占据态数目增加,费米面以上的非占据态数目也增加,所以电子吸收光子的跃迁概率大.这表明当电荷的转移率与电磁场的频率发生共振时,在回路中产生比较强的光电流.从方程(13)可知,光电导的吸收峰出现在ω∼λE+λC,这也是光电导的峰值随着温度的升高而降低和峰值发生红移的原因.

图4 InAs和GaSb的厚度均为8 nm时,不同温度下的光电导(实线为T=4.2 K时的光电导,虚线为T=77 K时的光电导,点线为T=300 K时的光电导)Fig.4. The conductivity at different temperatures with LInAs=LGaSb=8 nm(The solid line,dashed line and dotted line represent the conductivity at the temperature 4.2,77 and 300 K,respectively).

4 结 论

本文系统地研究了量子阱结构对基于InAs/GaSb的二类、断带半导体量子阱中光电导性质的影响,光电导的峰值位置可以通过量子阱的结构调节,研究发现当量子阱中InAs和GaSb的厚度均为8 nm时,光电导的峰值落在太赫兹区(0.2 THz).在该量子阱体系中有电子和空穴两种载流子,光电导主要由费米面附近的载流子跃迁引起,由于电子的有效质量小,电子在费米面附近的跃迁对光电导贡献最大,但当调节量子阱的结构,如LInAs=8 nm,LGaSb=15 nm时,量子阱中的空穴浓度很大,因此空穴跃迁对光电导的贡献起主导作用.本文进一步研究了温度对光电导的影响,研究发现,温度升高,光电导的峰值有所下降并且峰值发生红移,这主要是因为温度对费米面附近载流子的占据态有重要的影响.本文运用平衡方程的方法来求解玻尔兹曼方程得到体系中的光电导,该方法既可以避免弛豫时间近似带来的误差,又简单可行,可以为基于InAs/GaSb的二类、断带半导体量子阱系统在太赫兹光电器件方面的研究提供依据.