质子在碳化硅中不同深度的非电离能量损失

申帅帅 贺朝会 李永宏

(西安交通大学核科学与技术学院,西安 710049)

1 引 言

随着半导体技术的发展,半导体器件在航空航天、宇宙探索和核工业等领域的使用越来越广泛,这使得辐照环境下半导体器件的性能和可靠性研究成为重点领域[1].碳化硅作为第三代半导体材料的代表[2],相比于前两代半导体材料硅、镓和砷化镓等,具有禁带宽度大、热导率高、电子饱和漂移速率高、击穿场强高、抗辐照能力强等优越性质[3−6],这使得碳化硅在电子器件的制备方面具有广泛的应用前景,而抗辐照电子器件和辐射探测器等产品的研发也备受重视.此外,碳化硅优良的热稳定性、抗辐照特性、机械性能和化学稳定性,使其能够在堆内强中子辐照环境下保持性能稳定,也成为堆内结构的理想材料[7].

粒子辐照引起材料内的晶格原子位移,产生位移损伤效应,会导致半导体器件性能逐渐丧失甚至失效[8],而半导体器件在辐照环境中的位移损伤主要依赖于灵敏体积内沉积的位移能量损失值.大量实验研究表明,对于大多数电子器件,当入射粒子的类型不同时,位移损伤引起的半导体器件的性能变化和非电离能量损失(non-ionizing energy loss,NIEL)均呈线性关系,因此,位移损伤的计算可以转化为NIEL的计算.通过计算不同能量的特定粒子在器件材料中的NIEL,可以评价不同粒子辐照下器件的性能变化情况.

通过解析计算和数值模拟等方法,前两代半导体材料,如硅、锗和砷化镓等,在不同能量质子辐照下的NIEL已经被研究较多.Chilingarov等[9],Lazanu等[10]和吴宜勇等[11]使用解析方法和实验方法分别计算了砷化镓和硅在多种离子辐照下的NIEL,发现探测器性能的下降可以归因于NIEL;朱金辉等[12]和唐欣欣等[13]结合软件模拟和解析方法分别对300 eV—1 GeV能量质子在硅中和低能质子在硅、砷化镓中的NIEL进行了计算;路伟等[14]和郭达禧等[15]使用Geant4软件分别对质子在硅中的NIEL和中子在碳化硅中的位移损伤进行了模拟计算;陈世彬等[16]运用分子动力学方法模拟了4H-SiC材料辐照下级联碰撞过程,发现空位缺陷的数量和空间分布与初级碰撞原子的能量呈线性相关.但作为第三代半导体材料代表的碳化硅,其相关研究相对较少.数值模拟研究中多使用薄靶近似的方法来进行NIEL的计算,而对于足够厚的结构材料内不同深度的损伤情况没有直观表现.因此,分析质子在碳化硅材料不同深度的NIEL,对研究碳化硅在质子辐照下不同区域的损伤差异有着重要意义.

2 计算方法与仿真模型

2.1 NIEL的计算

计算粒子辐照对半导体器件造成的位移损伤,关键是要得到粒子在器件材料中沉积的位移损伤能量.当入射粒子进入器件材料后,会与材料中的原子发生相互作用,包括核弹性、非弹性碰撞和核反应等,导致原子离位产生初级撞出原子(primary knock-on atoms,PKA)或产生核反应产物.由于核反应产物也会继续通过与原子核屏蔽库仑散射,从而与材料中原子发生相互作用,并传递足够高的能量使材料中原子产生离位,发生位移损伤,因此,初级反冲原子和核反应产物产生的位移损伤的机理一致,本文计算中将两者统称为初级反冲原子.初级反冲原子的反冲能T分为两部分,一部分引起电离或激发,另一部分引起了材料的位移损伤.位移损伤能量的部分通过Lindhard分离函数进行计算.

1963年,Lindhard等[17]引入近似输运动力学方程,使用Thomas-Fermi势计算弹性过程能量损失,并由此推导出NIEL的值SNIEL为

式中,σi为原子反应截面,Ti为第个反冲平均位移能量损失部分(Lindhard分离函数),NA为阿伏伽德罗常数,A为靶原子质量数.

1974年,Robinson和Torrens[18]修正了Lindhard函数,修正后的Lindhard分离函数Q可以表示为

这里,T为初级反冲原子能量,Q(T)为位移损伤所占比例,乘以T,就能得到位移损伤能量;Z和A为初级反冲原子的原子序数和质量数,ZL和AL则分别为器件材料原子的原子序数和质量数.

以上公式用于计算粒子在单质中的位移损伤能量,对于碳化硅这样的化合物,则需将器件材料中各元素的原子序数ZL和质量数AL进行原子密度加权平均,得到平均原子序数Zaverage和平均质量数Aaverage:

式中,ni为元素在化合物中的原子密度.

Akkerman等[19,20]计算了初级反冲原子能量低于200 eV后的Lindhard分离函数,将(5)式修正为(8)式:

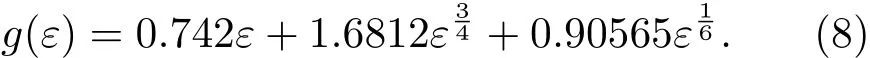
一般而言,当初级反冲原子能量大于200 eV时,使用(5)式计算初级反冲原子的损伤能量,否则用(8)式.

由上文可知,粒子在器件材料中的NIEL的计算,实际上为粒子与材料中原子发生核弹性、非弹性碰撞和核反应等相互作用产生的初级反冲原子的Q部分能量的均值.

2.2 模型建立

本文选用碳化硅为靶材料,通过Geant4程序模拟追踪质子在靶材料中的输运过程,获得质子入射碳化硅材料后的初级反冲原子的能量、空间位置和种类等信息,再通过修正后的Lindhard分离函数获得产生位移损伤的能量部分,进而计算得到NIEL值,并分析NIEL与入射质子能量的关系、NIEL在材料不同深度的变化规律、以及不同种类的初级反冲原子对NIEL的贡献及影响.

靶材料碳化硅密度为3.21 g/cm3,材料厚度根据不同计算要求进行设置.质子束垂直入射靶材料表面,入射质子的能量范围为1—500 MeV,在保证计算精度的前提下,考虑计算效率,根据不同计算要求将质子注量设置为106—108n/cm2.

3 结果与分析

3.1 质子在碳化硅中的NIEL

在NIEL的模拟计算中,为了保证质子在穿越靶材料的过程中能量衰减得尽可能少,需要将靶材料厚度设置得尽可能薄;但是为了获得足够的数据,降低统计误差,靶材料厚度又不能太薄.综合考虑,采用薄靶近似的方法建立靶材料模型,将靶材料厚度设置为每种能量质子相对应射程的10%,具体靶厚如表1所列.

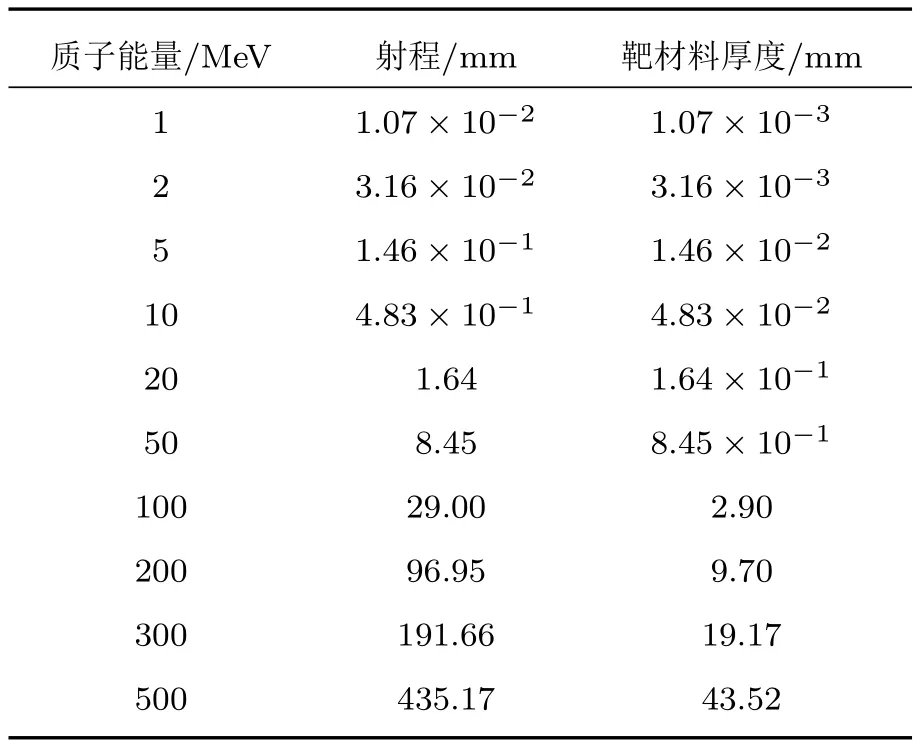
表1 质子在碳化硅中射程及靶材料厚度Table 1.Range of proton in SiC and thickness of target material.

质子辐照碳化硅的NIEL随入射质子能量的变化情况如图1所示,同时比较了Dale等[21]和Jun等[22]通过数值计算方法得到的质子在硅和镓材料中的NIEL,Si-G4代表本人使用Geant4软件模拟得到的质子在硅材料中的NIEL.

由图1可以看出,使用Geant4软件模拟得到的质子在硅中的NIEL与Dale等[21]和Jun等[22]计算得到的值相符.在1—500 MeV能量范围内,质子在各种器件材料中的NIEL值均随能量的增大而减小,说明低能质子辐照在器件引起的位移损伤相对较大.同时,通过比较质子在不同材料中的NIEL,可以看出,质子在碳化硅中的NIEL明显低于硅和镓中的值,说明同等质子辐照环境下,碳化硅材料制造的器件所受到的位移损伤要比其他材料小得多,即器件性能更加稳定、抗位移损伤能力更强.

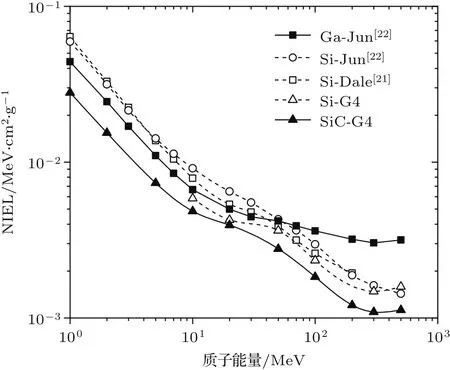
图1 质子在不同材料中的NIEL值Fig.1.NIEL of proton in different materials.

3.2 材料不同深度的NIEL

上节采用薄靶近似的方法计算了不同能量的质子在碳化硅材料中的NIEL,但这种计算方法并没有考虑NIEL在足够厚的结构材料中的变化.在本节的模拟计算中,将碳化硅靶材料的厚度设置成大于对应能量质子的射程,以保证质子能量在半导体材料中完全耗尽,进而分析NIEL在碳化硅材料不同区域的差异.

图2 不同深度的NIEL随质子能量的变化Fig.2.NIEL vs.proton energy in different depth.

质子在碳化硅材料不同深度的NIEL,有两个区域值得关注,一个是以薄靶近似计算NIEL的前端区域(10%质子射程),另一个是质子射程末端沉积大量能量的布拉格峰区域.图2对比了不同能量质子入射下,材料前端区域和布拉格峰区域的NIEL的变化规律.可以看出,入射质子能量在1—300 MeV时,前端区域的NIEL要比布拉格峰区域的值小,但这种差距随着能量的增大而逐渐缩小,当质子能量大于300 MeV之后,前端的NIEL反而超过了布拉格峰峰值.

碳化硅中辐照损伤最严重的区域会随着入射质子能量的变化而发生改变,为了分析这种变化的原因,进一步研究了不同能量质子在碳化硅中的初级反冲原子的种类分布以及不同种类初级反冲原子对总的NIEL的贡献.

3.3 不同种类初级反冲原子对NIEL的贡献

按照形成原因及数目占比把质子与靶材料相互作用产生的次级粒子分为28Si,12C和“其他”三类.28Si和12C为靶材料碳化硅自身原子被撞击离位产生,“其他”则多由核反应产生.由表2可以看出,28Si和12C两种粒子的数目在初级反冲原子中的占比随着入射质子能量的增加而逐渐下降,由主要产物变为次要产物,“其他”次级产物则逐渐成为主要产物.入射质子能量在1—100 MeV时,12C所占比例比28Si高,但两者占比随着质子能量的增加而逐渐接近,质子能量大于100 MeV后,28Si的占比反而超过12C.

为了研究不同能量质子辐照下不同种类初级反冲原子的数目占比变化以及对NIEL的贡献,根据模拟结果,选取具有代表性的三组质子能量10,100和500 MeV进行分析.模拟结果如图3—图5所示,其中,每组图左侧为不同质子能量下初级反冲原子数目占比随入射深度的变化规律图,右侧为对应的质子能量下不同种类的初级反冲原子对NIEL的贡献随入射深度的变化规律图.

10 MeV能量质子在碳化硅材料中产生的不同种类初级反冲原子的数目占比和不同种类反冲原子对总NIEL的贡献,随入射深度的变化,根据粒子类型不同而有所差异.10 MeV能量质子在碳化硅中产生的初级反冲原子以弹性碰撞离位的靶材料自身原子28Si和12C为主,而因核反应等其他反应产生的“其他”粒子则少得多.28Si和12C的数目占比随入射深度的变化呈现类似布拉格峰式的分布规律,在材料浅层,粒子数目占比随入射深度缓慢上升,而在射程末端急剧上升,表明在此处有大量初级反冲原子产生.“其他”粒子则由于数目占比较少,变化规律不明显,随入射深度的变化不大,但在射程末端也有相对其他深度较多的粒子产生.

表2 质子在碳化硅中的初级反冲原子种类分布Table 2.PKA type distribution of protons in SiC.

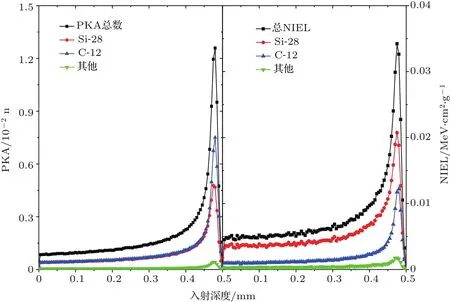
图3 10 MeV质子在碳化硅中产生的不同初级反冲原子的数目占比和对NIEL的贡献Fig.3.PKA type distribution and the contribution to NIEL vs.the incident depth of 10 MeV protons in SiC.

图4 100 MeV质子在碳化硅中产生的不同初级反冲原子的数目占比和对NIEL的贡献Fig.4.PKA type distribution and the contribution to NIEL vs.the incident depth of 100 MeV protons in SiC.

10 MeV质子产生的不同种类的初级反冲原子对总NIEL的贡献与初级反冲原子的类型息息相关.28Si和12C导致的NIEL呈明显的布拉格峰分布规律,且对NIEL的贡献占主要部分,虽然28Si的数目占比小于12C,但28Si对NIEL的贡献却超过12C,即单个28Si初级反冲原子造成的NIEL要大于12C.“其他”种类的初级反冲原子由于数目占比较少,对NIEL的贡献也相对较少,随入射深度的变化不明显.

由图4可以看出,当质子能量达到100 MeV时,不同种类初级反冲原子的数目占比随入射深度的变化产生了较大变化.28Si和12C的数目占比已经基本相等,且随入射深度的变化规律不变,即类似布拉格峰的分布规律.“其他”种类的初级反冲原子数目占比大幅提升,在材料浅层甚至超过了28Si和12C,但“其他”种类的初级反冲原子的数目占比随入射深度的变化依然不明显,只是在射程末端出现了下降.相对应的不同种类反冲原子对总NIEL的贡献有了较大改变,“其他”种类的初级反冲原子对总NIEL的贡献在材料浅层已经超过28Si和12C的贡献,但其对总NIEL的贡献随入射深度的变化仍不明显,在射程末端同样出现了下降.“其他”种类的初级反冲原子数目占比的大幅提高,相对布拉格峰抬升了材料浅层的总的初级反冲原子数目占比和总的NIEL.

由图5可以看出,当入射质子能量达到500 MeV时,“其他”种类的初级反冲原子已经成为质子在碳化硅中产生的初级反冲原子的主要部分.“其他”种类的初级反冲原子的数目随入射深度迅速下降,这是由于其主要由核反应产生,当质子能量达到500 MeV时,高能质子在碳化硅材料中发生大量核反应,并产生次级产物,导致其数目迅速增多.质子在碳化硅材料中的能量随入射深度增大而逐渐降低,导致核反应减少,进而引起核反应产物的迅速减少.“其他”种类的初级反冲原子的数目随入射深度的变化规律也反映到对总NIEL的贡献上,其造成的NIEL也是随入射深度增加而迅速下降.28Si和12C的数目占比和对总NIEL的贡献随入射深度的变化仍然保持不变,即在浅层随入射深度缓慢上升而在射程末端出现布拉格峰,只是无论粒子数目占比还是对总NIEL的贡献已经远低于“其他”种类的初级反冲原子.

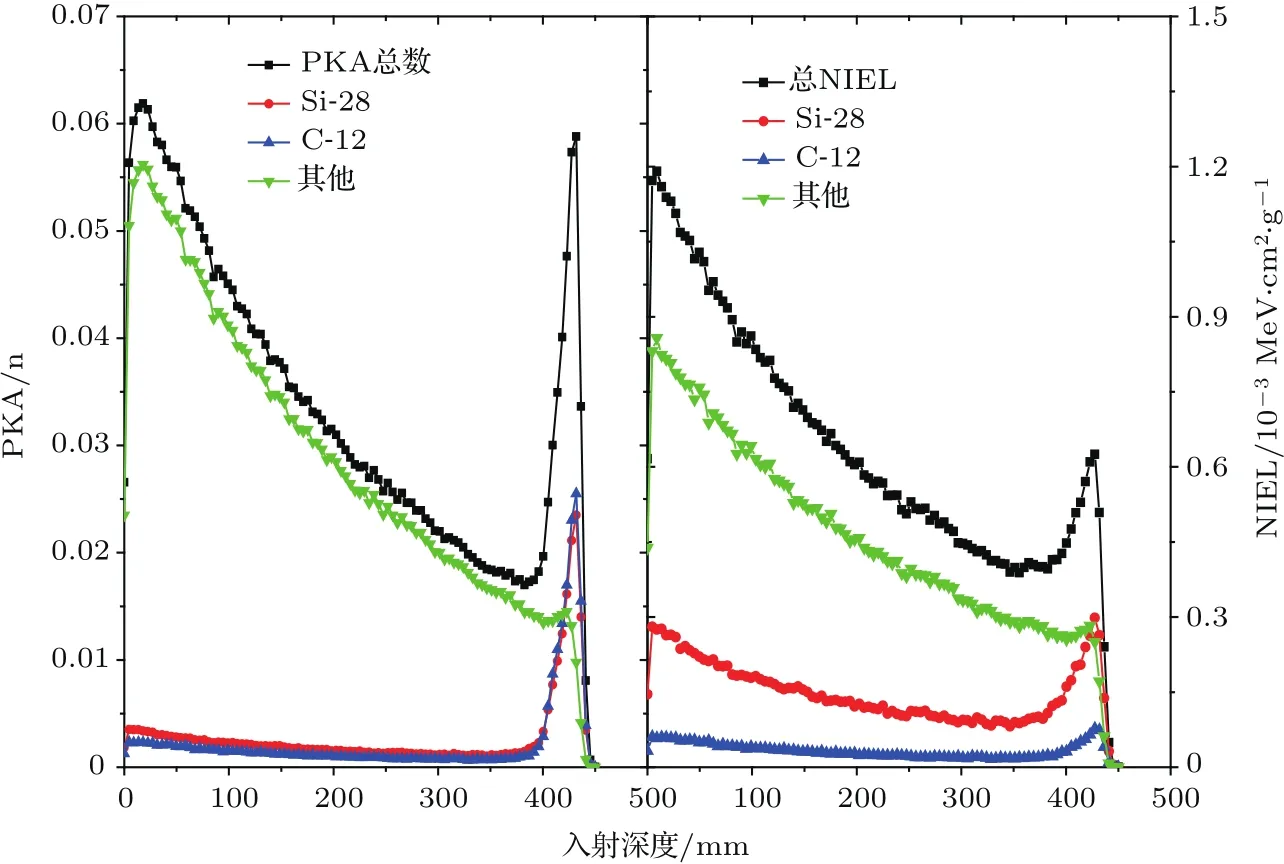
图5 500 MeV质子在碳化硅中产生的不同初级反冲原子的数目占比和对NIEL的贡献Fig.5.PKA type distribution and the contribution to NIEL vs.the incident depth of 500 MeV protons in SiC.

综上所述,入射质子能量较低时,质子在碳化硅中的位移损伤主要由28Si和12C造成,且由28Si造成的损伤明显高于12C;而质子能量增高后,虽然NIEL的布拉格峰仍然由28Si和12C造成,但相对于布拉格峰,迅速抬高的前端平坦区则是由于核反应等产生的“其他”次级离子所造成.二者结合,导致随着质子能量的增大,材料损伤最严重的区域从质子射程末端前移到材料表面.

4 结 论

本文通过Geant4软件,采用薄靶近似的方法模拟计算了碳化硅材料中NIEL与质子能量的关系,探究了在靶材料足够厚的情况下,NIEL随材料深度的变化情况,并根据不同种类的初级反冲原子数目占比分析了这种变化形成的原因.

质子在碳化硅材料中的NIEL模拟计算结果表明,在相同辐照环境下,碳化硅材料中的位移损伤相比硅、镓等材料更小,证明碳化硅器件具有更好的稳定性以及更高的抗位移损伤能力.

通过分析碳化硅材料不同深度的NIEL值,得到了不同能量质子辐照下,材料损伤最严重的区域,模拟结果表明,材料中损伤最严重的区域与入射质子能量相关,低能质子辐照下,位移损伤最严重的区域出现在质子射程末端,但随着质子能量的增加,这一区域会逐渐前移直到材料表面.

初级反冲原子的数目占比和对NIEL的贡献随入射深度的变化规律,揭示了损伤区域随质子能量变化的原因.模拟结果表明:入射能量较低时,质子辐照碳化硅中产生的28Si和12C是位移损伤的主要影响因素;随着质子能量的增加,28Si和12C仍是射程末端布拉格峰形成的主要成因,但通过核反应等过程产生的次级离子数目占比增加,其造成的位移损伤占总损伤的比例在材料浅层区域增大,导致材料表面成为位移损伤最严重的区域.