部分相干光束经过湍流大气传输研究进展∗

王飞余佳益刘显龙蔡阳健

1)(苏州大学物理科学与技术学院,苏州 215006)

2)(苏州大学,苏州纳米科技协同创新中心,苏州 215006)

3)(山东师范大学物理与电子科学学院,光场调控及应用中心,济南 250358)

1 引 言

自由空间激光通信是以激光作为信息载体,在不同的平台(地面平台、空对地平台等)之间开展信息传递与交换的一种技术.与传统的无线电波通信相比,激光通信在很多方面具有一定的优势:1)激光频率高,具有超大带宽,能极大地提高信息传输速率;2)激光方向性好,在一定程度上能提高信息传输的安全性,同时还具有较强的抗干扰能力;3)激光亮度高、发散角小,同时,激光器体积小,易于集成,方便搭载于不同平台上.除了自由空间光通信,以激光为载波的激光雷达、远程遥感也有独特的优势.然而,在这些应用中,激光都是以自由空间(大气)作为信息传输通道,大气中的微粒和分子对激光的吸收和散射及湍流对激光造成的光斑漂移、光强闪烁等效应,严重影响通信系统的性能.因此,激光在大气中的传输特性及大气本身性质的研究显得尤为重要.

当光波在大气中传输时,将受到大气的影响发生吸收、散射及大气折射率随机变化导致的相位随机起伏等现象.吸收和散射主要是由组成大气的分子、大气中的悬浮颗粒及气溶胶等引起的,并使得光波在传输路径上的能量发生衰减,吸收和散射的强度依赖于光波的波长.大气不规则的随机运动,每一点上的压强、速度、温度等物理特性的随机涨落通常称为大气湍流.它的存在导致大气的折射率随机起伏,湍流中传输的光波的振幅和相位也随之发生无规则的起伏,是影响光波传输特性的主要因素.通常情况下,大气湍流将引起光波发散角变大、光束展宽、光斑位置随机抖动、相干性退化以及到达角起伏等效应,严重影响自由空间光通信和激光雷达等系统的信息传递和交换性能.因此,国内外研究人员开展了大量激光束在大气中的传播行为及如何克服或抑制大气湍流引起光波扰动的研究工作.

从物理上来讲,大气湍流是一种非线性的随机过程,其严格解可由著名的Navier-Stokes(N-S)方程导出,然而,从数学上严格求解N-S方程至今仍是一个难题.1941年,苏联学者Kolmogorov[1]发展了一种运用统计学方法描述湍流的统计规律,虽然这种统计方法对实际复杂的湍流运动过程做了一些简化和近似,但是比起理论上严格求解N-S方程,这种方法显得更为简易和方便.我们现在所知的光波在湍流大气中的传输理论研究,几乎都是基于Kolmogorov的湍流统计理论发展而来的.

另一方面,部分相干光理论经过Zernike,Wolf,Gori及Friberg等几代科学家的发展和完善,已经形成了一套比较完善的理论框架.部分相干光束也已经被广泛地应用在惯性约束核聚变、激光扫描、非线性光学等领域.高斯-谢尔模光束是部分相干光中最为熟知的一种模型(光强分布和相干度分布都满足高斯分布),被广泛应用于各种理论和实际计算中.目前,研究部分相干光束传输的主要方法有张量方法、二阶矩方法、高阶矩方法、Wigner分布函数方法和数值计算等方法.

2000年以来,受到自由空间光通信等应用的推动,大气湍流效应抑制的研究成为一个重要的课题.目前已知的抑制技术和方法有:大孔径接收技术、编码调制技术、自适应光学方法、部分相干光束作为信息载体传输方法等.作为一种重要的湍流效应抑制方法,部分相干光束在湍流大气中的传输特性的研究重新引起了国内外研究人员的重视,已有大量关于部分相干光束在湍流大气中传输特性的研究文献发表,推动了湍流理论和光传输理论的进一步发展.特别是近几年来,光场调控逐渐成为光学领域的热点研究课题之一,部分相干光束的相干结构、相位和偏振调控理论及技术都得到了长足的发展,多参量调控的部分相干光束与湍流大气的相互作用也逐渐成为一个重要研究课题.

本文第2节回顾了部分相干光束在湍流大气中传输研究的历程和进展;第3节简要介绍了部分相干光束在湍流中传输的理论模型及二阶统计特性,包括平均光强、相干度及光束发散角等二阶矩的计算方法;第4节主要介绍部分相干光在湍流大气中的相位屏数值模拟方法;最后简要展望了部分相干光束在湍流大气中传输研究今后的发展方向.

2 部分相干光束在湍流大气中传输研究回顾

光波在湍流介质中传输理论的研究可以追溯到激光器发明之前,在1960年和1961年,苏联学者Chernov[2]和Tatarskii[3]分别发表了讨论光波在湍流介质中的光束展宽、光强闪烁、相干性演化等特性的著作.从那时起,各国学者对光波在湍流大气中的传输行为进行了深入的研究,详细讨论了光波在湍流中的强度分布、光束漂移、光斑展宽等物理特性.这期间主要的理论研究方法包括:Rytov微扰法、差分方程法、梯度近似法、几何光学近似方法等[4−6],研究对象主要是球面波、平面波和高斯光波.1971年,Lutomirski和Yura[7]引入了一种新的方法,就是现在熟知的广义惠更斯-菲涅耳积分法,处理有限孔径的平面波在湍流介质中的传输问题.1972年,Yura[8]运用这种方法得到了高斯光束在湍流介质中传输后的互相干函数,在一定条件下可以退化到平面波和球面波情况.广义惠更斯-菲涅耳积分法可以方便地处理不同模式的光束(包括部分相干光束)在湍流中的平均光强、光束展宽、相干性退化等特性,因此目前仍被研究人员广泛采用并用来研究部分相干光束在湍流大气中的传输行为.实际上,早在1967年,苏联学者Feizulin和Kravtsov[9]就独立地发展和运用广义惠更斯-菲涅耳方法研究了高斯光束在湍流大气中的光束展宽.

1972年,Kon和Tatarskiis[10]研究了部分相干光束(高斯-谢尔模光束)在湍流大气传输过程中有效相干长度及光束的初始相干长度对光束平均光强的影响,这可能是最早的关于部分相干光束在湍流大气中传输行为的研究文献.1978年,美国学者Leader[11]基于广义惠更斯-菲涅耳原理的瑞利-索末菲积分公式得到了高斯-谢尔模光束在湍流大气中传输的互相干函数和平均光强的解析表达式,并研究了相干特性和光强在湍流中的演化.随后,Wang和Plonus[12]结合广义惠更斯-菲涅耳原理和Rytov相位结构二次近似方法得到了在弱湍流条件下高斯-谢尔模光束的互相干函数的普适表达式,在他们的研究中,还考虑了初始光源准直特性.除了部分相干光束的光束展宽、平均光强、相干性等二阶统计的建模,研究人员也开始关注理论上更难处理的部分相干光束在湍流介质中的光强起伏(闪烁)特性的研究.1981年,Leader[13]研究了在弱湍流条件下任意尺寸大小的准直或聚焦的部分相干光束在传输过程中光强闪烁因子,研究中运用了广义惠更斯-菲涅耳积分和湍流中球面波四阶关联统计的方法.随后,Wang等[14]运用和Leader类似的方法进一步考虑了在接收面为有限孔径(孔径平滑效应)的条件下部分相干光束经过弱湍流大气传输后的光强闪烁因子.苏联学者Banach等[15,16]在此期间也研究了部分相干光束在湍流大气中的光强闪烁,其研究分成两种类型,即探测器的响应时间快于和慢于部分相干光束本身光强变化速度,发现两种类型对实验探测到的光强闪烁有重要的影响.然而在此期间,学者们的研究重点放在理论研究上,实验研究成果较少.理论研究发现在满足“慢探测器”的前提下,部分相干光束与完全相干光束相比,能有效地降低湍流引起的光强闪烁,具有重要的应用价值.在1990—2000年,部分相干光束在湍流大气中传输特性的研究似乎突然被研究人员忽视了,只有少数的研究成果发表[17,18].

从2002年开始,受到自由空间光通信、激光雷达等应用发展的影响,部分相干光束在湍流介质中的传输行为又重新引起了研究人员的兴趣.Gbur和Wolf[19]从理论上研究了部分相干光束在湍流介质中光束平均光斑半径的演化,并从这个角度揭示了部分相干光束受到湍流的影响比相同条件下的相干光束小.随后,Dogariu和Amarande[20]利用热板模拟大气湍流效应,从实验上验证了部分相干光束的平均光斑半径展宽受到湍流的影响比相干光束小,并随着光束相干长度的减小而进一步减小.Shirai等[21]利用部分相干光束的相干模式分解,研究了该光束在湍流介质中的光束展宽和平均光强分布,并从模式分解角度解释了该光束受到湍流扰动较小的物理原因.同期,美国陆军实验室Ricklin和Davidson[22,23]着眼于部分相干光束在自由空间通信中应用的可能性,对部分相干光束在弱湍流中的平均光强、相干性演化、光强闪烁等特性做了进一步研究,并从理论上分析了误码率和光束相干性的关系,得到低相干性光源能大幅降低误码率的结论.Korotkova等[24]利用激光束经过随机扰动屏模拟部分相干光束,得到了计算光强闪烁因子的解析形式,并分析了该光束在湍流大气中的光强闪烁因子和误码率的大小,也得到了与文献[23]类似的结论.此后,国内外学者对部分相干光束及其他类型的光束在湍流介质中传输的研究投入了极大的热情,每年有大量的研究文献发表.

这一时期,研究人员关注的重点是光束的模式、偏振态、相位等与湍流介质相互作用引起的一些特异的传输特性.各种模式的光束,如拉盖尔-高斯光束[25]、双曲余弦高斯光束[26]、厄米-余弦-高斯光束[27],椭圆高斯光束[28],径向偏振光束[29]、贝塞尔-高斯光束[30]、艾里光束[31]、涡旋光束[32]等,在湍流大气中的平均光强、光束展宽、光斑漂移等特性得到了详细的研究.尽管初始的光波模式不尽相同,研究人员得到的结论可以归纳为:1)光束在湍流大气中传输足够远的距离时,光强分布逐渐退化成高斯分布,与初始光束的光强分布无关,且湍流强度越大,退化成高斯分布的传输距离越短;2)光束发散角和光束展宽随湍流强度的增加而增大.与此同时,研究人员还把目光转向各种类型的光束阵列在湍流大气中平均光强和发散角特性[33−39],研究发现与单束光波相比,阵列光束也能有效抑制湍流引起的光强闪烁[40,41].在部分相干光束湍流传输方面,不再是考虑单纯的高斯-谢尔模光束的传输特性,与完全相干光束类似,研究人员把光束的偏振态及模式与相干性结合起来考虑在湍流大气中的平均光强演化、光束发散角等二阶统计特性.相干性和光波模式结合各类高阶部分相干光束,包括带扭曲相位的部分相干高斯-谢尔模光束[42,43]、部分相干高阶高斯光束[44−51]、部分相干平顶及空心光束[52−55]等的平均光强和光束发散的统计特性得到了广泛的研究.同时,部分相干部分偏振光束(随机电磁光束)在湍流大气中的偏振特性演化、平均光强演化特性也得到了深入的研究[56−67].一个比较有意思的研究结果是随机电磁光束在湍流大气中传输时,光束在远场的偏振度的值会恢复到光源面的偏振度的值[58],但这个结果至今还未得到实验证实.

由于光强闪烁与信息传输的误码率直接相关(光强闪烁越小,误码率越低),因此光强闪烁因子的研究具有更实际的意义.从理论上来讲,光束光强闪烁因子的计算比光束平均光强、发散角等二阶统计要复杂得多,而且基于广义惠更斯-菲涅耳原理和Rytov四阶复相位统计理论得到的结果与从近轴波动方程出发得到结果是不相符的.一般认为从近轴波动方程出发得到的结果更为接近实际结果,所以基于广义惠更斯-菲涅耳原理得到的部分相干光强闪烁因子结果只能从一定程度上得到一些正确的结论.但由于这种方法能够得到近似的解析解,还是被很多研究人员采用.基于此理论,人们研究了一些不同类型的部分相干光束,如部分相干平顶光束[68]、随机电磁光束[69]、部分相干多高斯光束[70]、贝塞尔关联光束[71]、带扭曲相位部分相干光[72]等的光强闪烁因子.研究结果表明,这些部分相干高阶光束的光强闪烁因子在相同条件下比高斯-谢尔模光束的低.但需要注意的是,部分相干高阶光束的发散角在同等条件下比高斯-谢尔模光束的大,似乎是牺牲了接收端的能量达到降低闪烁因子的效果,这个结果在完全相干高阶高斯光束中也适用.

近年来,光场调控成为光学领域的热点研究课题之一,部分相干光束的相干调控研究引起了国内外众多研究人员的兴趣,一系列具有不同相干结构的部分相干光束模型被理论建模[73].部分相干光束相干结构与湍流介质相互作用引发的一些新特性及新效应的研究成为一个重要的课题.各类具有特殊相干结构的部分相干光束在湍流大气中传输的平均光强、质量因子、光束扩散等特性得到了深入的研究[74−87].由于受到湍流和相干结构两个因素的影响,这类部分相干光束在湍流介质中的平均光强首先会演化成一些特殊的形状,如平顶分布、空心分布等,然后逐渐退化为类高斯分布.值得指出的是,在同等条件下,特殊相干结构的部分相干光束的发散角比传统的高斯-谢尔模光束要大.这类特殊相干结构的部分相干光束在湍流介质中的光强闪烁因子更值得关注,尤其是非均匀关联光束,它在自由空间中传输会出现类似于“自聚焦”的现象[88].Gu和Gbur[89]研究了弱湍流中非均匀关联光束的光强闪烁因子,结果发现在合适的参数下,该光束比传统的高斯光束不仅具有更低的闪烁因子,而且中心区域的光能量更大,这就解决了部分相干光束发散角过大导致光能量发散较快的问题.我们课题组在理论上研究了多高斯关联光束在弱湍流大气中的光强闪烁因子,发现这种光束也能有效降低闪烁因子[90],该实验结果被美国迈阿密大学Korotkova及美国海军学院Avramov-Zamurovic教授在户外实验中验证[91,92].

总体而言,近几年有关激光束经过湍流大气传输的研究文献主要关注不同初始参数(如偏振、相位和相干结构)的激光束与湍流介质相互作用后的统计特性,研究的目的一方面是探讨不同类型的光源与湍流相互作用的基本物理特性,更为重要的是期望调控光源的参数达到一些更优的效果,比如更低的光强闪烁、更高的能量接收效率等.

3 部分相干光束经过湍流大气的传输模型

3.1 部分相干光经过湍流大气传输的平均光强和相干性统计特性

大气层中空气无规则的运动导致空气的气压、温度、密度等无规则起伏称为大气湍流.而大气的折射率取决于上述参数,因此大气的折射率也随空间和时间做无规则的变化,光波在湍流中的效应主要表现为强度起伏(光强闪烁)、相位起伏(相位的空间、时间起伏)和光束漂移(方向起伏)等.一般而言,湍流属于弱散射介质范畴,因此光束的后向散射效应及偏振退化(耦合)效应可以忽略不计;再者,我们还需要假设在光束传输方向上折射率起伏的关联函数服从狄拉克函数分布.运用上述假设,从经典电磁理论出发,光波在湍流中的标量亥姆霍兹方程表示为

式中,U(R)表示光束的某一个电场分量;R≡(x,y,z)是空间三维坐标,其中光束假定沿z方向传播;k=2π/λ是光波的波数,λ是光波波长;n(R)=n0+n1(R)表示湍流介质的折射率分布,其中n0≈1,n1(R)表示折射率的起伏变化,⟨n1(R)⟩≈0,角括号表示对系综(时间)的平均.根据湍流统计理论,折射率起伏在空间两点R1和R2的协方差函数可以表示为

式中,R≡(r,z),r≡(x,y)表示与z轴垂直平面内的笛卡尔坐标;Bn表示折射率起伏协方差(相关)函数,根据Kolmogorov湍流统计理论,在湍流惯性区域,协方差函数正比于两点距离差的2/3次方.等式最右边运用了马尔可夫近似(Markov approximation),即:在光波传输方向上,折射率起伏服从狄拉克函数分布,An(r1−r2)是二维的协方差函数.

方程(1)最为人熟知的两种处理方法是Born微扰法和Rytov扰动方法.Born微扰法是把光波电场分量写成各级散射波的求和:

式中,U0(R)表示未被扰动(散射)的电场分量,U1(R)和U2(R)分别表示一级和二级散射分量.与此相对应的是,Rytov扰动方法是考虑电场分量受到一个复相位的扰动,写成如下形式:

式中,ψ(R)表示由湍流引起的复相位扰动,也可写成如下级数形式,

ψ1(R)和ψ2(R)分别表示一级和二级复相位的扰动.对比(3)和(4)式,Born和Rytov方法的不同点是:Born方法把扰动场表示成求和形式,而Rytov方法把扰动场表示为“相乘”形式.以往的研究中,Born方法成功地用于各种弱散射物体散射场的计算,但是在湍流领域普遍使用的是Rytov方法研究光波经过湍流介质的统计特性.究其原因,可能是Born方法更适用于短距离的散射问题,而Rytov方法更适用于光波长距离传输的微扰.早期的关于光波在湍流介质中的传输研究大多是基于Kolmogorov湍流统计理论,借助于Rytov方法从亥姆霍兹(近轴传输方程)出发讨论光波的统计性质,得到了一些非常基础性的结果[2,3],但是这种方法的数学要求较高,对于复杂高阶光束以及部分相干光束,很难从数学上严格的求解.

进入21世纪以来,研究人员更倾向于用Lutomiriski和Yura[7]发展的广义惠更斯-菲涅耳积分方法处理光波在湍流大气中的统计特性.这种方法的优点是可以方便地处理各类不同的光波模式,如高阶高斯光束、平顶光束等复杂激光束在湍流介质中的特性,而且在弱湍流和强湍流条件下,所得到的平均光强、光束发散角等性质能较好地符合实验结果[93],甚至在做了二次方近似之后仍与实验结果较好地符合[94].

图1是光波在湍流介质中从入射面到出射面的示意图.根据广义惠更斯-菲涅耳原理,在湍流介质中入射面和出射面上的光波电场满足如下积分关系:

式中,L表示从入射面到出射面的传输距离;r和ρ是与传输轴垂直的入射面和出射面的位置矢量;U0(r,0)和U(ρ,L)分别表示入射面和出射面上光波的电场分量;ψ(r,ρ,L)表示的是从入射面到出射面由湍流介质引起的Rytov复相位扰动,根据惠更斯-菲涅耳原理,在出射面上的光波是入射面上每一点发出的球面波的相干叠加,所以ψ(r,ρ,L)实际代表的是球面波情况下Rytov复相位扰动.在实际应用中,人们更关注的是光波的平均光强、发散角等物理量,对(6)式取复共轭,然后乘(6)式,取系综平均后得到

式中,是光波任意两点之间的系综平均,在部分相干光范畴内,通常称为互相干函数,包含了光波的相干信息,如果是完全相干光,不需要进行系综平均运算;是出射面上的互相干函数,包含光束的平均光强、相干性等信息;等式最后一项尖括号内表示的是由湍流引起的复相位扰动的二阶统计平均;尖括号中的下标“s”和“m”分别表示光源本身的振幅和相位的起伏和湍流引入的复相位二阶统计.根据Kolmogorov湍流统计理论和Rytov微扰(只考虑到二阶微扰),(7)式最后一项可以表示为[95]

其中,ρd=ρ1− ρ2和rd=r1−r2分别表示出射和入射面上的位置矢量差;κ是空间频率矢量κ≡(κx,κy)的模,κ与空间坐标r组成傅里叶变换对;J0是零阶贝塞尔函数;Φn(κ)表示湍流谱密度,是(2)式协方差函数的傅里叶变换.其中最为人熟知的湍流谱密度函数是Kolmogorov谱,它的表达式为

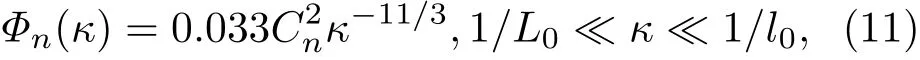
式中,是折射率结构常数,是衡量湍流强弱的一个参数,通常情况下,当时,称为“弱湍流”,当时,称为“强湍流”这种对湍流强弱的划分方法也不是绝对的,因为湍流的强弱也与在湍流中的传输距离密切相关;L0和l0是湍流的外尺度和内尺度常数.(11)式适用的条件只是在湍流的惯性区域,即谱空间频率值在内尺度和外尺度数的倒数之间.如果假定外尺度为无穷大,湍流谱在κ非常小时发散(趋于无穷大),为了在计算上更好地应用,Tataskii和von Karman对湍流谱进行了数学上的扩展,使之能包含全部的空间频率,又不含有奇点.现在常用的湍流为von Karman湍流谱,其表达式为

其中κm=5.92/l0,κ0=C0/L0,C0的值根据具体条件可以取不同的值,一般为2π—8π,其他湍流谱的模型可以参考文献[96].在现实环境中,大气湍流在不同的地理区域,同一天不同的时间段及不同的气象条件下都是不同的,而且从物理上而言,它的统计特性并不是严格静态的,统计特性随时间的变化而变化,所以用固定的湍流谱模拟光波的统计性质只能从一定程度上反映光波的变化.(12)式的湍流谱还可以扩展到non-Kolmogorov情况.需要指出的是,在得到(9)和(10)式的前提是运用了马尔可夫近似条件及假定湍流是各向同性的.把(9)和(10)式代入(7)式,一般来说是很难得到解析表达式的.为了得到近似的解析表达式,还需要引入一些近似条件,对(10)式做进一步简化.一种常用的简化是认为(10)式中的积分函数只在贝塞尔函数的变量κ|(1−ξ)ρd+ξrd|≪1范围内有值,其他区域的值趋于0,在这个条件下,贝塞尔函数可以只取泰勒级数的前两项作为近似值,即:J0(x)≈1−x2/4.把这个条件代入(10)式,积分后可以得到如下解析式:

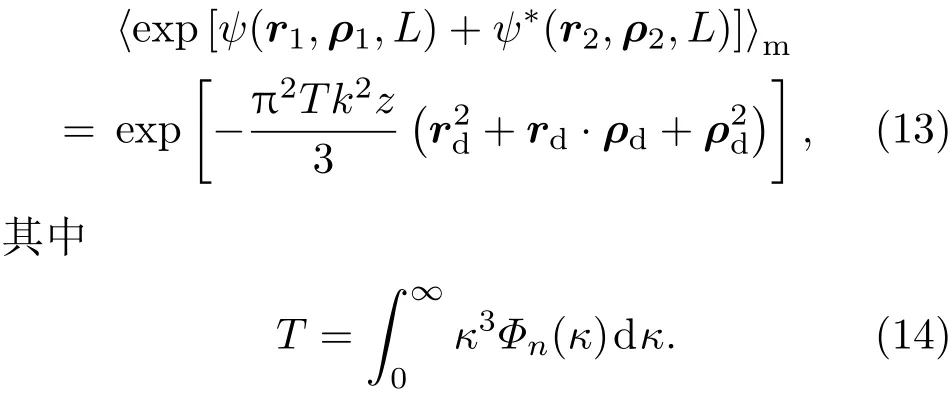
运用(13)式,大部分的部分相干光束模型在湍流介质中的平均光强和相干性分布都能得到解析形式,可以比较方便地分析这类光束的平均光强及相干性的演化过程.值得注意的是,运用贝塞尔函数级数展开的前两项作为近似是在强湍流条件下得到的[21],现有的部分文献并不遵照这个条件使用级数展开研究部分相干光束的二阶统计特性,从一定程度上来说会引入一定的误差.另外一种在大气湍流介质中常用的二阶复相位扰动统计模型是基于球面波在湍流中的波结构函数并结合二次近似条件[22]:

其中,D是从入射面到出射面的球面波结构函数;()是球面波在湍流大气中传输的相干长度.如果湍流谱为Kolmogorov谱的形式,从数学上得到的严格解是ρ0的5/3次方,而不是2次方的形式,但是为了计算的方便,大多数文献采用了二次方近似条件.由二次方近似而引起的计算误差一般都在可接受的范围内.

图1 光波从入射面经过湍流大气到达出射面的示意图Fig.1.Schematic for the propagation of light beams through turbulent atmosphere from input plane to output plane.

3.2 部分相干光束在湍流大气中的平均光斑宽度及发散角

光波在湍流介质中传输的光束平均光斑宽度及发散角的变化能提供光束能量发散快慢的信息,同时也能计算光束在传输过程中的质量因子的演化.光束的平均光斑宽度和发散角根据定义可以从光束的平均光强信息中直接得到,更全面地计算部分相干光束在湍流大气中阶矩的统计信息,需要借助于部分相干光束在湍流介质中的Wigner函数.四川大学张彬课题组[97]得到了部分相干光束在湍流介质中传输过程中光束二阶矩矩阵,可以方便地得到各类光束的任意阶矩信息.光束在传输过程中的平均光斑宽度定义为[21]

根据文献[19],光束的平均半径可以表示成如下普适的形式:

(17)式右端第一项表示光束的初始(光源面)的光斑宽度;第二项表示的是光束在自由空间中传输过程中由衍射引入的光斑发散,与传输距离的平方成正比,是自由空间中远场发散角;第三项表示的是由湍流介质引入的光束的额外发散,与传输距离的三次方成正比,其中

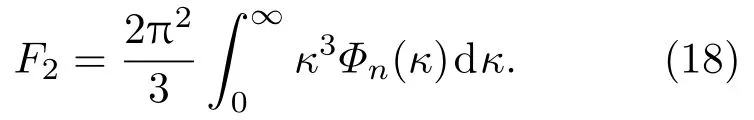
(18)式表明第三项只与湍流特性有关,而与光束的初始状态无任何关联.这就是说,在传输距离足够大或者湍流强度足够强(F2足够大),光束的平均光斑半径只取决于第三项,即湍流引起的光束扩散,而且几乎所有光束的平均半径都是一致的,与光束的初始参数无关.如果初始光斑是椭圆形状,在湍流大气中椭圆率会逐渐减小,最终变成近似圆形.

要得到部分相干光束任意阶矩的信息,最方便的方法是借助于部分相干光束的Wigner分布函数:

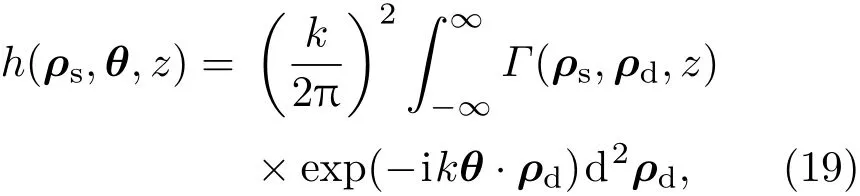
其中,ρs=(ρ1+ρ2)/2,Γ(ρs,ρd,z)是部分相干光束在出射面上的互相干函数,θ是与部分相干光束平均发散角相关的一个量.从Wigner函数出发,光束沿x轴和y轴的平均光斑半径及发散角阶矩定义为

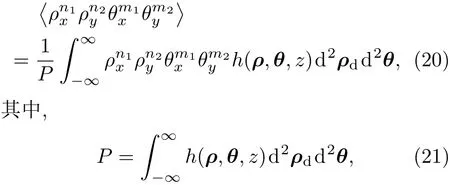
P表示光束所携带的总能量.根据(20)式,部分相干光束的任意阶矩都可以求得.利用Wigner函数分布具体计算部分相干空心光束、部分相干平顶光束及扭曲部分相干光束的二阶矩的方法,可参考文献[55,98,99].

3.3 部分相干光束在湍流大气中传输的光强闪烁

光波在湍流介质中的传输效应,除了光束发散角变大、相干性退化、光斑位置的随机漂移等,最主要的是光强随时间发生随机变化(光强起伏).晚上我们观察某些星星时,会发现星星“眨眼睛”现象,这就是星星“发出”的光经过地球大气湍流引起的光强起伏.在自由空间光通信中,这个由湍流引起的随机光强起伏是导致系统误码率上升的主要因素.通常,用闪烁因子定义光强起伏的强弱:

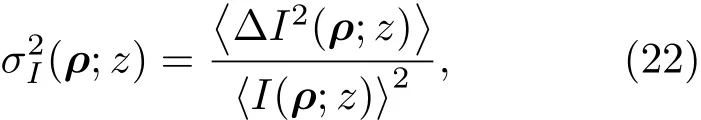
式中,是接收面上ρ点处的瞬时光强;是平均光强;尖括号表示对系综的平均.从(22)式看出,闪烁因子是光强起伏的归一化协方差.

对于部分相干光束来说,需要考虑三个特征时间的大小:1)部分相干光束自身光强扰动的特征时间τs;2)大气湍流介质随时间变化快慢的特征时间τa;3)探测器探测光强的积分时间τd.这三个特征时间的大小,将会大幅度影响探测到实际的光强闪烁因子的大小.如果τd≫τs,探测器“感受”不到部分相干光束自身的光强扰动,如果τd≪τs,那么探测器能感知部分相干光束自身引起的光强扰动.据此可以把探测器分成两类,一类是“快探测器”,满足条件τd≪τs≪τa,即探测器的探测时间要远小于部分相干光束自身光强扰动时间和湍流介质变化的时间,它可以同时探测到湍流引起的和光源自身扰动导致的光强变化;另一类是“慢探测器”,满足τs≪τd≪τa,即探测器的探测时间介于湍流介质变化特征时间和部分相干光束自身光强扰动时间,这里部分相干光束自身引起的光强变化时间要远远小于湍流介质变化时间,所以探测器测量只是湍流介质引起的光强起伏.现阶段大部分研究部分相干光束在湍流介质中的光强闪烁特性的文献都是基于“慢探测器”原理而建立起来的理论框架进行的.基于广义惠更斯-菲涅耳原理,部分相干光束在湍流介质传输过程中入射面和出射面上的四阶统计特性的关系如下:

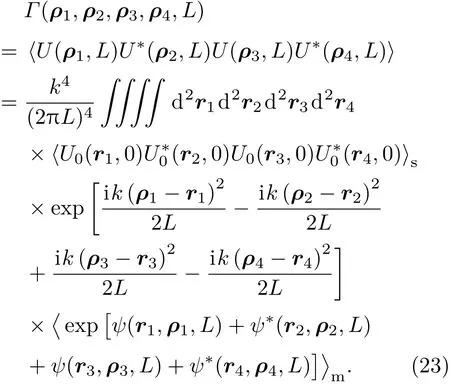
(23)式积分中尖括号下标“s”和“m”分别表示对部分相干光束自身引起光强起伏的平均和湍流介质复相位扰动引起的统计平均.在慢探测器理论框架下,并假定部分相干光束的复振幅变化满足高斯统计,这样我们可以把部分相干光束的四阶统计简化为

其中Γs为入射面上光束的互相干函数.湍流介质引起的复相位四阶统计可以简化为

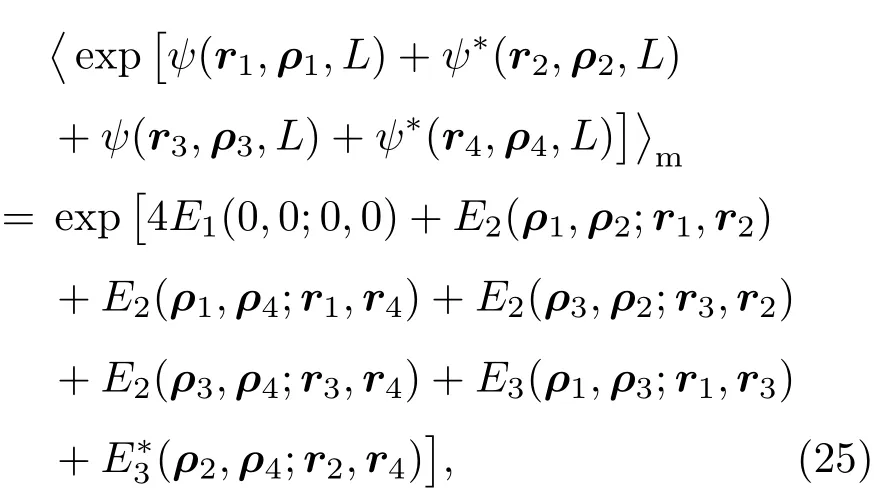
E1和E2表达式见(9)和(10)式,E3表达式为

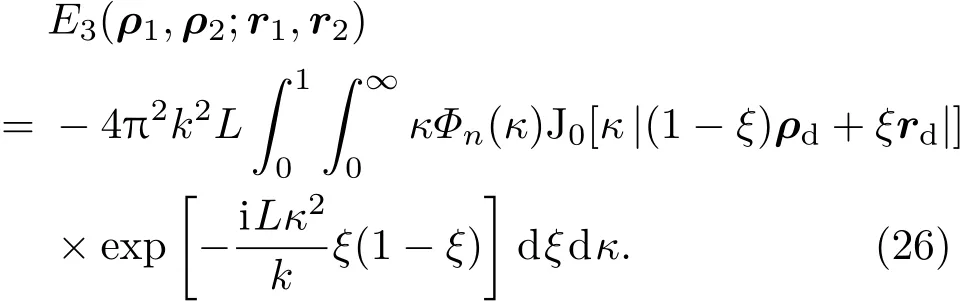
但是,(25)式过于复杂,利用(25)式很难得到部分相干光束在湍流介质传输过程中的解析表达式.一种可行的方法是对(25)式简化,得到一些近似表达式.目前较多的是在弱湍流近似下,(25)式可以近似表示为

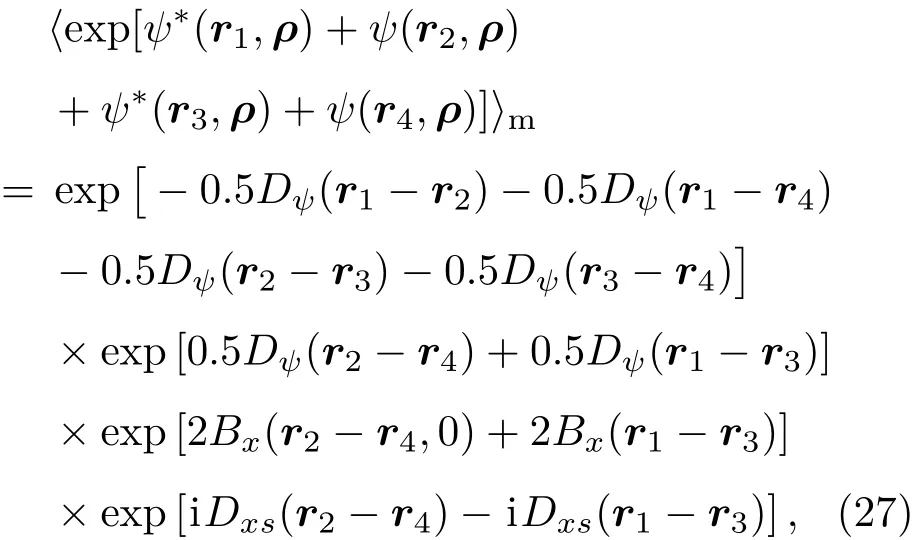
式中,1,2,3,4)是球面波的波结构函数;是振幅对数相位结构函数;是球面波对数振幅和相位的相干长度;是对数振幅关联函数;是球面波对数振幅方差.基于(27)式,可以计算一些相对简单的部分相干光束模型的光强闪烁因子[41,72,100],但是对于一些复杂的部分相干光束,依靠(27)式还是很难得到解析式.

除了上述方法之外,另外一种计算部分相干光束在湍流中的闪烁因子的方法是在完全相干光束的出射面上放置一个满足高斯统计的随机相位屏,结合湍流介质的谱特性,这种方法成功地得到了高斯-谢尔模光束和随机电磁光束的光强闪烁因子[24,69].从原理上来说,这种方法可推广到其他更为复杂的部分相干光束情况,但是这个推广至今还未见文献报道.2006年,Berman和Chumak[101]报道了另外一种光子流概率密度的方法计算部分相干光束的闪烁因子.

近几年,本课题组开展了一些部分相干光束经过实验室模拟湍流后的光强闪烁因子的实验研究.相比于同等条件下的部分相干光束,附加一个涡旋相位(部分相干涡旋光束)后能有效地降低光束经过湍流后的光强闪烁因子,并且光强闪烁因子还随着涡旋拓扑荷数的增加而减小[102].除了相位的影响,我们还研究了部分相干径向偏振光束经过湍流介质后的闪烁因子,与涡旋相位类似,叠加径向偏振后,光强闪烁因子也进一步减小[103].

4 部分相干光经过湍流大气传输的相位屏数值模拟方法

4.1 随机相位屏模拟完全相干光束在大气湍流中的传输

在第3节,我们主要回顾了基于广义惠更斯-菲涅耳原理和Rytov微扰理论计算部分相干光束经过湍流介质的传输特性.由于Rytov方法是基于长时间统计平均后的特性,所以只能计算光波在湍流介质中的平均统计特性,即平均光强、光斑半径等,而无法得知光束“瞬时”的强度特性.根据实验测量的数据,高斯光束经过湍流介质传输后出射面上的光强是偏离高斯形状的,会发生光斑变形、扭曲,在强湍流条件下,光斑会瞬时分裂成几个或多个散斑.

多相位屏是目前运用最广泛的模拟光波经过湍流大气传输的数值模拟方法,该方法不仅可以得到光束的平均光强、相干性演化及光强闪烁因子等二阶和四阶统计特性,还能得到光束的瞬时光强分布.在这一节中,先介绍多相位屏方法的原理,然后再探讨把多相位屏方法运用到部分相干光束.相位屏方法的原理和方法在文献[104]中已经有详细的描述和介绍,先简单回顾该方法的原理和流程.从(1)式所表达的湍流中的亥姆霍兹方程出发,如果考虑的光束是沿z方向传输的傍轴光波,那么U(R)可以写成如下形式:

其中,R≡(x,y,z),V(R)是关于z的缓变函数.把(28)式代入(1)式,运用湍流折射率起伏n(R)=n0+n1(R)关系,经过化简得到如下傍轴近似下光束传输方程

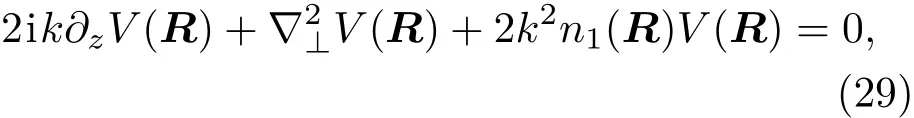
其中,(R)是湍流折射率起伏,其平均值为零.从(29)式可以看出湍流的扰动来自于第3项.如果只考虑自由空间光波的传输方程(第3项为零):

其中,r≡(x,y).对(30)式中的V(r,z)做关于r的傅里叶变换,得到

其中,κ≡(κx,κy)是r对应的空间频率;函数F是V的傅里叶变换.(31)式从z′面传输到z平面的一个解可以表示为

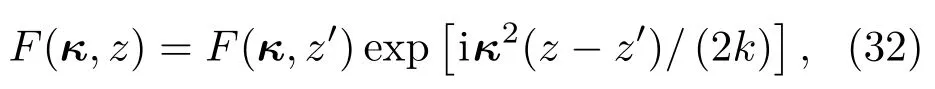
根据几何光学,在实空间相位随机扰动的关联函数可以表示成

图2 光波在多相位屏中传输的示意图Fig.2.Schematic for light beams propagating in the multi-random phase screen.

把(2)式代入(33)式,利用狄拉克函数的积分特性得到:

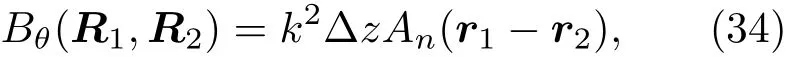
An(r1−r2)是与传输轴垂直的平面内湍流折射率扰动的协方差(关联)函数,与湍流谱密度的关系为

根据(33)—(35)式,可以得到湍流中相位关联谱密度与折射率关联谱密度(相位关联函数的傅里叶变换)的关系:

根据(36)式,只要给定湍流的折射率谱密度函数,就能通过数值方法得到相位屏上的随机相位.具体计算方法如下:首先产生N×N行和列的满足方差为1的高斯统计随机数,然后产生的随机数矩阵与相位关联谱密度的平方根相乘,其中∆k=2π/(N∆),∆为离散的空间频率的最小间隔(一个像素点大小).最后对相乘后的矩阵进行二维离散傅里叶变换得到复数相位的矩阵θ1+iθ2.θ1和θ2任取一个都可以作为相位屏的随机相位矩阵.这样相位屏数值模拟方法的具体流程如下:

1)对发射面上光束的电场做傅里叶变化,通过自由空间传输到达第1个相位屏前,

2)光束穿过第1个随机相位屏,受到相位屏的相位扰动,

3)对电场做傅里叶变换,光束再通过自由空间传输到达第2个相位屏前,

4)光束穿过第2个随机相位屏,受到相位屏的相位扰动,

如此循环,直到通过所有的湍流随机相位屏.上述各式中,∆z=z/m,z是光束的传输距离,m为湍流随机相位屏的个数;θi(ri)是第i张湍流随机相位屏的扰动相位.到达接收面的光波的电场分布认为是通过湍流介质后的瞬时电场,要用数值模拟法得到光波的平均统计特性,需要生成n组(每一组包含m个相位屏)相位屏组合放置在传输路径上,n组之间的电场认为是不相干的,利用这n组电场就可以计算平均光强、相干性变化及光强闪烁因子等特性.

在数值模拟中,相位屏间隔的距离∆z之内属于弱湍流的范畴,一般来说,是用平面波在∆z距离之内的Rytov方差(平面波的闪烁因子)0.1来简单的判定.并且,另一个需要满足的条件是在传输距离∆z内Rytov方差是整个传输距离Rytov方差的10%以内.在合成相位屏幕过程中,由于Kolmogorov湍流谱:在κ→0时趋于无穷大,在零频附近,湍流谱随κ的变化而急剧变化,而数值模拟中一般是等间隔采样的,这样导致在零频附近湍流谱的误差增大,为了减小在零频处的误差,研究人员提出了一些采样方法来修正零频附近的误差[104,105].

4.2 部分相干光束经过湍流大气传输的相位屏模拟方法

与完全相干光不同,部分相干光束一般是用交叉谱密度函数或者互相干函数来描述它的统计特性,而不是直接以光束的电场来描述,所以相位屏模拟方法无法直接应用到部分相干光束的情况.一种可行方法是相干模式分解方法,即把部分相干光束看成是不同模式的完全相干光束的非相干叠加[106],

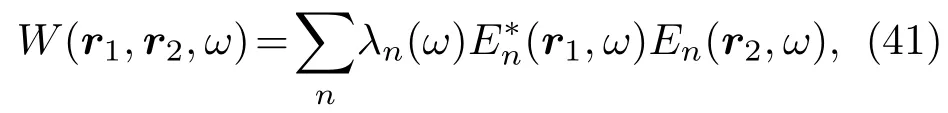
式中,W是部分相干光束的交叉谱密度;ω是光波的圆频率;λn(ω)是非负的本征值,代表模式的权重;En(r,ω)表示其中一个模式的电场.利用(41)式,把组成部分相干光束的每一个模式分量经过同样的n个相位屏组传输进行数值模拟计算,然后非相干叠加,得到部分相干光束的统计特性.然而,对任意的部分相干光束进行(40)式的模型分解并得到对应的解析解还有一定的难度,目前只有少数几种部分相干光束、如高斯-谢尔模光束,带扭曲相位的高斯-谢尔模光束有解析形式的模式分解[107,108].

另外一种方法是在完全相干光束的光源面上设置一个满足一定统计特性的随机相位屏(随机相位屏的制作方法与湍流随机相位屏的方法一致,只是谱密度函数不同)来模拟部分相干光束[109],但是纯实数的随机相位屏只能用来模拟相干性分布是高斯函数的部分相干光束,研究人员利用这个类型的随机相位屏开展了高斯-谢尔模光束、部分相干平顶涡旋光束经过湍流大气传输的相位屏数值模拟计算[110,111].纯相位屏虽然可以在实验上通过空间光调制器方便地产生,但是由于纯相位屏的相位关联函数与所产生的部分相干光束的相干函数并不一致,导致在数值计算上只能模拟关联函数为高斯函数的部分相干光束,存在一定的局限性.复数屏(光源的振幅和相位同时进行调制)能很好地克服这一缺点[112],复数屏的关联函数严格地等于部分相干光束的关联函数,因此可以用来模拟任意相干结构的部分相干光束.假设一完全相干光束经过复数屏调制后的电场为

其中,E0(r,0)是调制前的光场的复振幅;T(r)为具有一定空间关联特性的随机复透射函数(复数屏),假设T(r)满足高斯统计,其一阶统计平均为零,二阶统计只依赖于两点间的距离变化,

∆r=r1−r2,二阶统计平均为对应的光源的空间关联(相干)函数.

数值模拟产生复屏的方法与产生随机相位屏的方法类似,首先我们需要获知部分相干光场的空间关联函数的功率谱密度函数,对空间相干度函数进行傅里叶变化,即

其中,f是空频域矢量.在傅里叶域中,复屏又可以表示为功率谱密度函数的平方根和零均值、单位方差的复高斯随机数的乘积,即

在湍流理论中,一般假设光源的振幅、相位变化时间要比探测器的积分时间小很多;探测器的积分时间要比湍流引起的相位变化时间小很多,即τs≪τd≪τa,也就是说探测器仅仅只测量湍流引起的光束特征随时间的变化.基于这个关系,部分相干光束在大气湍流中的数值模拟逻辑过程表述如下:

1)湍流相位屏的合成,然后固定在传输路径上(湍流相位屏的合成上文已提及);

2)通过K1张复屏合成部分相干光束,并使每一帧(一张复屏)电场单独通过由多相位屏模拟的大气湍流(上文提及)到达接收面;

3)在接收面接收K1帧经过多相位屏的电场,并对K1帧电场取平均,得到的平均值就是通过大气湍流之后的一帧部分相干光束;

4)步骤1—3循环K2次,得到K2帧部分相干光束通过大气湍流的结果,可以利用这K2帧结果分析计算部分相干光束通过大气湍流之后的统计特性.

上述数值模拟方法也可以推广用来处理部分相干矢量光束经过湍流大气传输.

5 总结与展望

本文回顾了部分相干光在湍流大气中传输行为的研究进展、基本传输模型理论及相位屏模拟的数值方法.与完全相干光束相比,部分相干光束在湍流大气中传输能有效抵抗湍流带来的光束展宽、光斑漂移、光强闪烁等负面影响.但是,也应该注意到这种抵抗负面效应的效果是牺牲了接收面上的能量接收率,因为同等条件下,部分相干光束的发散角比完全相干光束要大.惟一例外是非均匀关联光束,在合适的参数下,它不仅具有较低的光强闪烁因子,而且有较高的能量接收效率,但是如何高效地产生这类非均匀关联光束[113,114],目前还是一个难题.

近年来,光场调控受到越来越多研究人员的关注,逐渐成为光学领域的热点研究课题之一.光场的多维调控,包括振幅、相位、偏振、相干性等的方法和技术越来越成熟,这些特殊调制光场在湍流大气中的传输行为及与湍流介质的相互作用是值得重点研究的一个课题,特别是利用光束的某些特性变化反演大气湍流的参数.近几年,关于部分相干光束在湍流中的研究文献大多是关于理论计算和数值模拟研究光束的传输行为,相应的实验研究文献较少.开展户外部分相干光束在湍流大气中的实验研究还需要进一步加强,这有待于部分相干光束的产生和调控技术的相对成熟.