微动条件下材料磨损率的一种计算分析方法∗

杨晓丽 王斌容 胡海云

(北京理工大学物理学院,北京 100081)

1 引 言

微动一般是在机械振动、疲劳载荷、电磁振动或热循环等交变载荷作用下,接触表面间发生的振幅在微米量级的相对运动.在结构工程中如各种连接件、各种紧固和夹持机构、各种弹性支撑机构、振动环境下的零部件等广泛存在微动现象.微动可以直接导致表面磨损,造成零件松动、功率损失或噪音增加,也可能由于磨屑聚集造成运动副咬死,有时也会引起灾难性事故.所以对微动磨损的研究具有现实意义,也越来越受到国内外学者的广泛重视[1].

磨损直接表现为物体表面材料的损失,因此,磨损过程中材料磨损率的研究对微动磨损的分析具有重要的意义.郝宏伟等[2]对高氮不锈轴承钢进行了不同应力和不同滑动速度下的微动磨损试验,得出试验钢的摩擦因数随应力和滑动速度的增加而减小;磨损率随应力和滑动速度的增加而增加.王璋等[3]对纯铁开展了球/平面接触模式下的冲击微动磨损试验,在增大冲击能量的条件下,磨损体积、磨损率也随之提高.丁燕等[4]对钛合金TC4-DT在不同试验条件下的抗微动性能进行了研究,并以磨损量、摩擦因数为指标分析了其微动摩擦磨损特性.张德坤等[5]对6×19点接触式矿用提升钢丝绳进行了钢丝的微动磨损试验研究,以摩擦系数和磨损深度作为评定微动磨损的参数,分析了不同载荷下摩擦系数的变化规律以及载荷、循环次数的变化对钢丝试样磨损深度的影响.以上研究都是通过对具体材料进行磨损试验来分析磨损率,缺乏统一的、普适的理论对材料磨损率进行计算分析.

2017年第21届材料磨损国际会议[6]指出摩擦学建模方面的工作具有巨大的理论指导意义,是未来大力发展的课题.微动磨损过程中摩擦、黏着和磨损三者密切相关,均需了解发生在分子水平的非平衡过程决定的宏观行为.非平衡统计理论正是从微观机理出发,通过统计方法推导出宏观特性及演化规律的理论方法,而微动摩擦学系统的不可逆性、时变性和随机性正好符合非平衡理论模型建立的依据.本文借助不对称双势阱模型,利用非平衡统计理论提出了一种新的研究微动磨损过程中磨损率的计算方法,并进一步对磨损过程中磨损时间、材料的势阱宽度及载荷正压力对磨损率的影响进行了分析.

2 理论模型

2.1 不对称双势阱模型

将发生微动磨损的两种材料A和B的近表面部分看作一个摩擦副系统.其中,设材料A为软材料,材料B为硬材料.磨损表现为材料表面物质的损失,摩擦表现为阻碍相对运动的作用力及其产生的机械能损耗.也就是说,磨损影响系统的结构,摩擦影响系统的功能.本文重点研究的是微动摩损过程中磨损量的变化情况,因此,研究侧重于摩擦副表层材料的损失.

借鉴分子动力学[7,8]的基本思路,从纳米量级考虑粒子在摩擦副系统中的运动.因摩擦副系统中两接触材料的不同是微滑产生的条件(若组成摩擦副的材料相同,根据Hertz理论力学[9]分析,两接触体所产生的切向位移相同,则相对滑动就不可能发生),在界面处两不同材料能量发生了变化,因此可以假设两接触材料中的粒子处在不同的两个势阱中[10].

图1所示不对称双势阱模型的势能函数表达式为

当x=0时,U1(x)=U2(x);其中U(x)为摩擦副系统中材料的势能函数,U1(x)和U2(x)分别为两材料A,B的粒子处在各自势阱中的势能函数;x为两材料中粒子所在位置到材料表面的距离,x=0为两材料的接触表面,x=xa和x=xb分别表示两材料A,B的势阱底部;U(xa)和U(xb)分别为距两材料接触表面xa和xb位置粒子的势能;和分别与A,B两势阱的宽度有关.

图1 不对称双势阱模型Fig.1.Asymmetric double well model.

不对称双势阱模型中决定两势阱形状的量,如势阱底部最小值、势垒高度和宽度等由两材料A,B本身的性质决定,而在实际微动过程中,粒子在两势阱中的运动及转移受到两材料间的接触时间、法向载荷、滑移距等的影响.因此,两摩擦副间的磨损过程就可以看作态A(材料A)和态B(材料B)间粒子的转移.在无外界环境影响时,初态处于原势阱的粒子仍处在原势阱中,它们各自在本势阱中趋于定态.但在实际生活中,摩擦副系统所处的环境总会有涨落或势垒壁热能产生,这种环境引起不可避免的噪声使摩擦副系统处于振动状态,两摩擦副材料表面产生微滑,导致磨损,即微动磨损.在双稳态势中,振动引起系统中的粒子在亚稳态和稳态间转移,这个过程就是粒子在两个势阱间进行交换,使系统从局域平衡过渡到整体平衡的过程.

2.2 非平衡统计理论模型

统计力学方法[11]的起点是系统的微观结构和粒子间的相互作用,即系统的微观模型.一旦微观模型确定之后,原则上可以采用力学的方法分析出系统所处的微观状态.通过分析这些微观状态和宏观状态之间的对应关系,并引入适当的假设,求解方程,可得到表征系统特性的关键,即分布函数.由此可讨论系统的宏观平均特性,从而导出宏观量.

微动摩擦学系统是典型的开放的动态非线性复杂系统,具有很强的系统依赖性、时变性、随机性和不可逆性,系统的各组元间相互作用,微观结构的微小变化可引起宏观量的改变,这些性质正是使用非平衡统计理论的依据.因此可以从微动摩擦学系统的微观机理出发,基于非平衡统计理论,研究系统状态的变化规律.

当受到外界环境影响,使两材料的摩擦副系统处于振动状态下时,材料内部的粒子会不断运动.由于材料的相结构、缺陷及范性变形等的不均匀性,其微观结构可看成是平均结构背景上叠加了这种不均匀的涨落.平均结构是确定的,不均匀性涨落是随机的.粒子在运动过程的各阶段,因这种不均匀性涨落的随机存在,使其速率与所经途径有关且一直在随机变化.所以,可以将粒子的运动看成随机过程.描述这个过程的方程是一个随机微分方程,具体如下.

设t表示在振动作用下粒子在材料内的运动时间,x(t)表示t时刻粒子运动的位移,表示t时刻粒子的运动速率.由于摩擦副系统中的材料可看成是确定性背景结构上叠加了随机性涨落,故粒子的运动速率遵守以下广义Langevin方

程[12]:

其中k(x)为粒子运动速率的确定部分,即平均运动速率;f(x,t)为粒子运动速率的随机部分,即涨落运动速率.在一定外界振动条件下,k(x)由平均结构和外界振动共同决定;f(x,t)由不均匀性涨落决定.

由于粒子的运动只与当时及稍早的外界振动和材料微观结构有关,而与其更早的历史无关,故可将其运动过程看成一个马尔可夫过程.依据随机理论[13],低速率运动的粒子f(x,t)为乘性噪声,可表示为

式中β(x)为乘性因子;f(t)为白噪声,且f(t)是高斯分布,满足条件

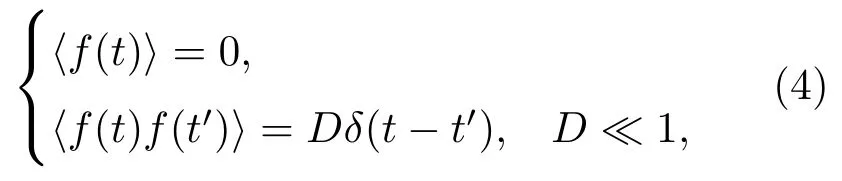
其中D为扩散系数.则(2)式变为

描述一个随时间演化的动力学系统通常用两种等价的方程:一种是动力学变量随时间演化的方程,即广义Langevin方程;另一种是概率密度函数随时间演化的方程,即Fokker-Plank方程.广义Langevin方程描述单个粒子转移,为了建立大量粒子的系统,可以得出相应的Fokker-Plank方程,从而推出势阱内粒子的概率密度分布情况.

根据随机理论,与Langevin方程对应的Fokker-Plank方程[14]为

其中P(x0,x,t)dx表示在振动环境下,初始距材料表面x0处位置的粒子在t时运动到距表面x和x+dx间位置的概率,P(x0,x,t)称为概率密度分布函数.

根据外界环境涨落和材料结构背景涨落的特性,对于(5)式中k(x),β(x)和(6)式中的D有如下关系:

其中τ为微动磨损的平均时间,η为总的相对偏差,A为与x无关的常量.则Foker-Planck方程(6)变为

3 计算结果与讨论

3.1 模型应用

对于稳态系统,在微动的初始阶段,黏着材料可能转移到对磨面上,也可能转移回来.对于不同材料配副,由于硬材料B的表面比较不易破坏,磨损主要发生在软材料A上,粒子从低强度低硬度表面转移到高强度高硬度表面.因此,我们以软材料A中的粒子为研究对象,粒子受到黏滞阻力、势阱力和随机力的作用.

初始时刻粒子处于势阱A中,其运动方程为

其中x为材料中粒子所在位置到材料表面的距离,v为粒子运动的速度,λ为耗散系数,−λv为黏滞阻力,U(x)为势能函数,为势阱力,F(t)为涨落力.

微动磨损过程中,摩擦副系统内两材料间相对位移很小,类似于高黏度情况,所以可近似认为与(12)式联立可得

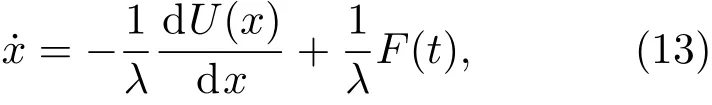
此处,为方便计算,可设黏滞系数λ=1,则(13)式变为

由不对称双势阱模型的函数(1)式知,材料A中粒子在势阱A中的势能函数为

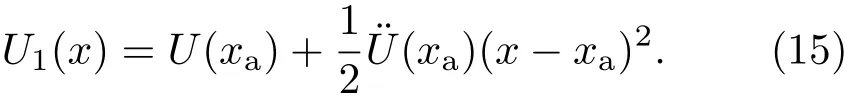
将(15)式代入(14)式得粒子在势阱A中运动的Langevin方程为

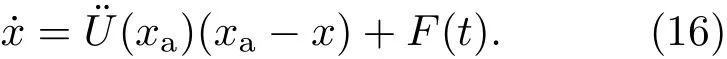
由(5),(7)和(16)式可得

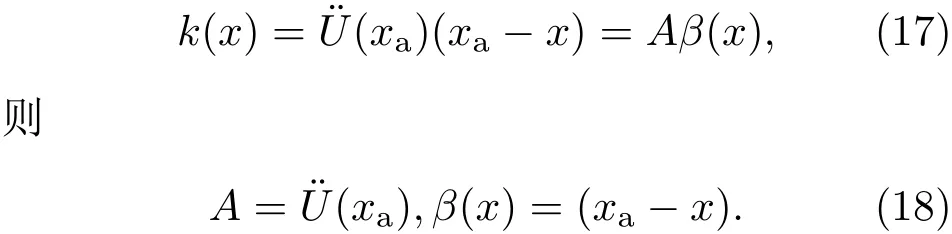
根据(8),(10)和(18)式,对于材料A内在势阱A中运动的粒子,其概率密度分布函数为

其中τA为粒子在势阱A中运动的平均时间.

同理分析可得,对于材料B内在势阱B中运动的粒子,在振动环境下,粒子的概率密度分布函数为

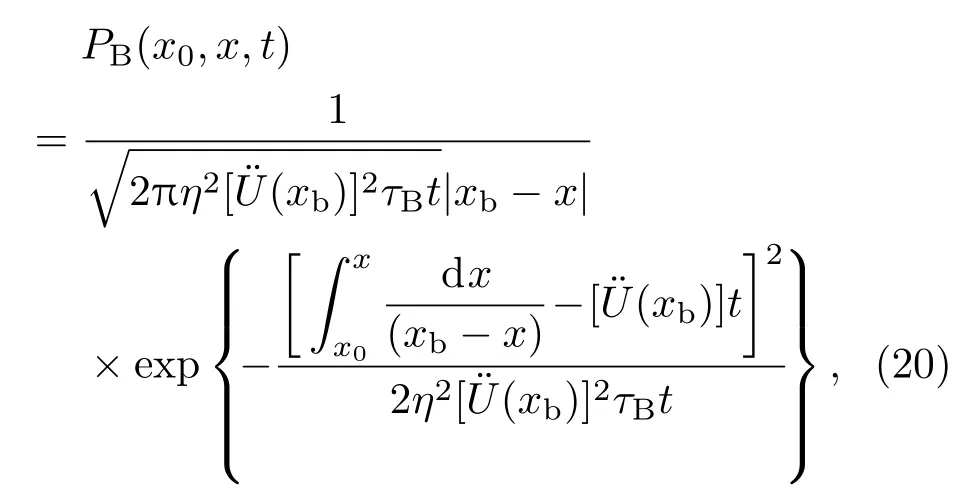
其中τB为材料B内粒子在势阱B中运动的平均时间.

3.2 计算与结果分析

将模型应用于由金属材料Mg(材料A)和Fe(材料B)组成的摩擦副系统.由于微动磨损主要发生在两接触材料的近表面部分,因此仅研究距材料表面微米量级位置的粒子在势阱中的运动.故在双势阱模型表达式(1)中,取两材料接触表面x0=0 m,表面势能U(x0)≈2×10−19J,两材料A,B势阱底部位置的值分别为xa=−2×10−6m,xb=2×10−6m. 根据文献[16]中数据可得材料A(Mg)和B(Fe)的势阱底部势能分别为U(xa)≈−1×10−19J,U(xb)≈−3×10−19J.计算可得:10−7J/m2.

在整个微动磨损过程中,粒子运动的平均时间τ满足

将(18)式代入(21)式,并代入数据可解得粒子在势阱A中运动的平均时间τA=2×107s.同理,可计算出粒子在势阱B中运动的平均时间τB=1.2×107s.

(6)式中P(x0,x,t)表示粒子从初始位置距材料表面x0处位置在t时运动到距材料表面x处位置的概率密度分布函数.因我们要研究的是微动磨损过程中材料的磨损,即粒子从材料内部到达材料表面的情况,所以可以用x表示材料表面,其值为0.将x0看作变量,其变化范围为要研究的势阱底部到表面部分,这里取为(−2×10−5,0]m和(0,2×10−5]m.

将上述数据分别代入(19)和(20)式并绘图,可得到不同情况下材料内各处粒子的概率密度分布情况.图2和图3分别为在势能函数不变的情况下,不同时刻摩擦副系统内两材料A,B中距材料表面不同位置的粒子可到达材料表面的概率密度分布;图4和图5分别为在时间不变的情况下,对于摩擦副系统中两材料A,B在不同势阱宽度下,各位置的粒子可到达材料表面的概率密度分布.

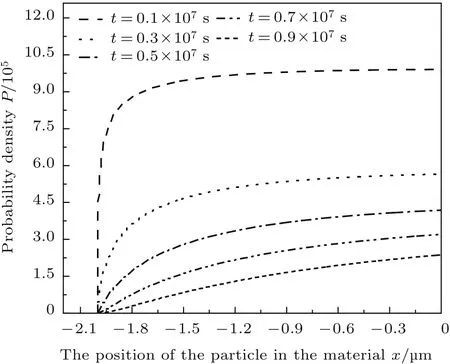
图2 不同时刻势阱A中概率总量随位置变化1.5×10−7J/m2)Fig.2.The probability density variation with position in potential well A

图3 不同时刻势阱B中概率总量随位置变化2.5×10−7J/m2)Fig.3.The probability density variation with position in potential well B

由图2和图3可知,在初始时刻,材料A,B中距材料表面[1.8×10−6,0]m范围内各处的粒子到达材料表面的概率几乎相同,且都比较大.随着时间的增加,同一位置的粒子,其到达材料表面的概率在逐渐减小;同一时刻,不同位置的粒子,越接近材料表面的粒子可以到达材料表面的概率相对越大,即越容易到达材料表面.这是因为在磨损初期,材料内粒子较活跃,相对容易被磨损掉而成为磨屑.随着时间的增加,磨损趋于稳定,离表面较远的粒子需受振动传递及一些力的影响,才能到达材料表面,而材料近表面的粒子由于直接受到外界振动的影响,所以较材料内部粒子更活跃,因此,更容易被磨损掉.总体来看,随时间的增加,材料总磨损率减小,磨损减轻.这与微动磨损理论[1]中,随着磨损的进行,有磨屑第三体的产生,磨屑起到润滑作用,使磨损减轻这一结论相符合.

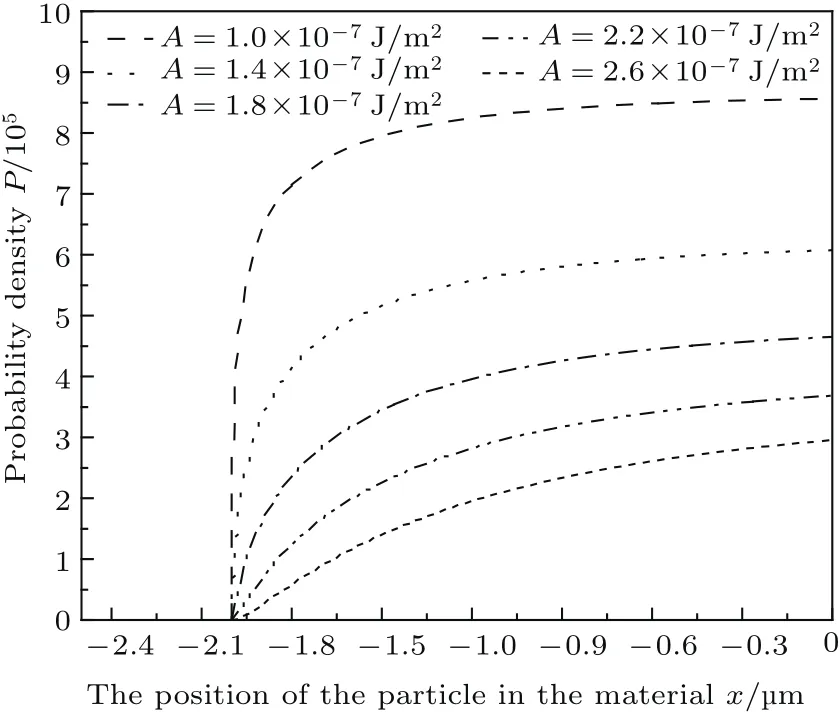
图4 材料A粒子在不同势阱宽度中概率密度随位置的变化(t=0.3×107s,势阱参量即A的值影响势阱宽度)Fig.4.The probability density variation with position in the A material(t=0.3×107s,the potential well parameteraffects the width of the potential well).

图5 材料B粒子在不同势阱宽度中概率密度随位置的变化(t=0.1×107s,势阱参量即A的值影响势阱宽度)Fig.5.The probability density variation with position in the B material(t=0.1×107s,the potential well parameteraffects the width of the potential well).

将图2和图4与图3和图5对比可得,距材料表面相同位置的粒子在同一时刻、相同势阱宽度的情况下,材料B中的粒子运动到材料表面的概率明显小于材料A.这是因为在摩擦副系统中,材料A是软材料,材料B是硬材料,由于材料本身性质的不同,软材料的粒子更容易由于微动而转移到达其表面,从而被磨损成为磨屑.

对(19)和(20)式中的概率密度分布函数PA(x0,x,t)和PB(x0,x,t)在摩擦副系统中材料A所研究的总范围[−2×10−5,0)m和材料B所研究的总范围(0,2×10−5]m内分别进行积分,可得在微动条件下材料内部的粒子从t时刻单位时间内运动到材料表面的总概率,即磨损率,表示为

根据(22)式,结合(19)和(20)式并代入数据计算可得磨损率大小.仅改变磨损时间,计算多组数据,绘图可得摩擦副系统中材料内粒子在势能函数不变时磨损率随时间的变化曲线,如图6所示.同样,仅改变表征势阱宽度的参量可得摩擦副系统中材料内粒子在相同时刻处在不同势阱中磨损率随势阱宽度的变化曲线,如图7所示.

从图6可以看出,摩擦副系统在磨损过程中两材料A,B的磨损率均随时间的增加而减少,而且刚开始减小得快,随后较慢并逐渐趋于稳定,这与微动摩擦学理论中的第三体理论[1](在磨损过程中形成磨屑作为第三体起到润滑作用而使磨损减轻,最后趋于平衡)相符合.从图7可以看出,在磨损过程中,摩擦副系统中两材料A,B的磨损率均随¨U(x)的增大而减小,即随着势阱宽度的变小而减小.这与前边概率分布随势阱宽度变化呈现出相同的规律,与势阱宽度变化引起势阱对粒子束缚力变化的现象相一致.分别对图6和图7中材料A,B的两条曲线进行对比可得:在摩擦副系统中材料A的磨损率始终大于材料B,这是因为这里选取的材料A为软材料,材料B为硬材料,在磨损过程中,由于材料本身性质的不同,软材料表面更容易发生磨损,材料中粒子更容易被磨损掉.但不管软材料还是硬材料,呈现的变化趋势相同.

图6 势阱中磨损率随时间的变化Fig.6.The change of wear rate in a potential well with time.

图7 材料中磨损率随势阱宽度的变化Fig.7.The change of wear rate in material with potential well width.

3.3 模型延伸分析

摩擦副间粒子相互作用的势能函数,其函数图像的形状与多种因素有关,包括接触载荷和滑移距等.这里通过建立势能函数和接触载荷的关系,可进一步得出其对磨损率的影响.

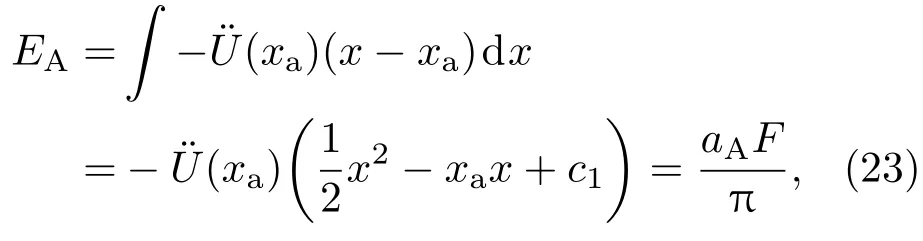
材料B的粒子在势阱B中有

其中,EA和EB为两材料A,B内粒子的势能;aA和aB分别为两材料A,B的晶格系数;F为载荷正压力;c1和c2分别为两材料A,B的积分常数.由(23)和(24)式可看出,对于材料内相同位置的粒子,与势阱宽度有关的量与载荷正压力F呈线性反比关系.由越大,势阱宽度越小,磨损率越小可知,载荷正压力越小,磨损率越小,反之载荷正压力越大,磨损率越大.磨损率随载荷正压力的变化如图8中的理论曲线所示,其变化趋势与磨损率随势阱宽度的变化趋势相同.开始阶段,接触载荷较低,微动磨损率变化幅值很小;当接触载荷增加到临界接触载荷后,微动磨损率随载荷的增加而急剧增大.

4 试验验证

通过以上内容的论证和计算,推导出了磨损率随势垒宽度和时间的变化关系,为了验证其合理性,将理论结果和试验结果[17]进行对比,如图8所示.

从图8可以看出,微动磨损率随载荷的增加而呈指数增长,理论计算结果与试验所得曲线的趋势基本一致,这进一步说明了理论的正确性.当载荷正压力较大时,理论计算结果和试验曲线有一定的差异,这主要是由于在理论计算中没有考虑边界条件等的影响.因磨损率表示单位时间材料内的粒子运动到材料表面的概率,故从材料磨损率能直接反映材料的磨损量.图8中理论曲线所反映的结论与有关磨损量随载荷变化的试验分析结果[18−21]相符合,从而也进一步证明了所得理论模型的准确性.

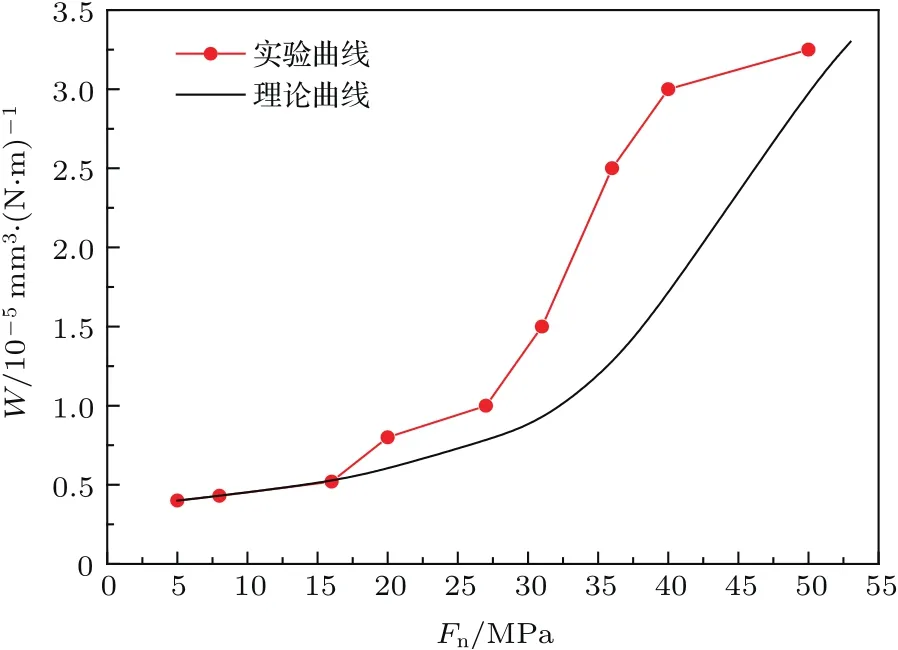
图8 载荷正压力磨损率的理论计算值与试验结果的比较Fig.8.The comparison between theoretical calculation and experimental of load positive pressure-wear rate.

5 结 论

建立了微动磨损过程摩擦副系统中粒子运动的非平衡统计理论模型,计算出了粒子在任意时刻从材料内部运动到表面的概率密度分布函数,求得了材料内粒子从t时刻,单位时间内运动到材料表面的总概率,即磨损率,进一步直接反映出材料的磨损量.同时,将理论模型应用于由金属材料Mg和Fe组成的摩擦副系统,从微观角度出发说明了磨损率随时间的变化和磨损率与势阱宽度的关系.结果表明:在相同摩擦副系统中,磨损率随时间的增大而减小;在相同时刻,势阱宽度不同的摩擦副系统,磨损率随势阱宽度的减小而减小.将势阱宽度与磨损率关系转化成载荷正压力与磨损率的关系,与已有试验数据结合对比,得出相同的结论,并与微动摩擦学中已有的磨损理论所得结论相符合,说明了该理论模型的正确性.

此模型适用于探究不同材料在微动过程中磨损率随一些影响因素的变化,从而达到对工业生产中一些仪器器件在微动磨损方面造成破坏的寿命预测,减少未知因素造成的损失.