一道圆中动点问题的解法赏析
2018-10-22江苏省张家港市乐余高级中学张新村
☉江苏省张家港市乐余高级中学 张新村
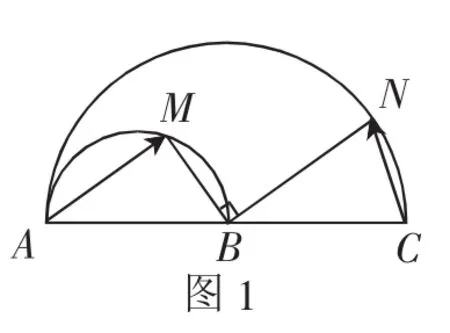
【模考真题】如图1,已知AC=2,B为AC的中点,分别以AB,AC为直径,在AC同侧作半圆,M,N分别为两半圆上的动点(不含端点A,B,C),且BM⊥BN,则的最大值为_____.
【思路点拨】本题主要考查圆上动点问题、向量垂直的充要条件、向量数量积的运算、最值问题等,解决问题的关键主要是对题设条件中BM⊥BN的处理,以及两个半圆的作用的分析,最终所求的最大值无非两种思路:一是转化成函数,求最大值;二是利用基本不等式求最大值.
一、解析几何法
题中既然提及“AC=2,B为AC的中点”,不妨考虑写出两个半圆的方程,设出动点M,N的坐标,最后转化成函数最值问题.
解法1:以点B为坐标原点,AC所在直线为x轴,建立平面直角坐标系,如图2所示.因为AC=2,B为AC的中点,所以A(-1,0),C(1,0),设动点M(x1,y1),N(x2,y2),易得以AB为直径的圆的方程为以AC为直径的圆的方程为x2+y2=1,所以整理得因为AB为直径,所以∠AMB=90°,因为BM⊥BN,所以∠MBN=90°,所以AM∥BN.而即

所以(x1+1)2(1-x22)=x22(-x12-x1),整理有x1=x22-1.
即(x1,y1)·(x2,y2)=0,所以x1x2+y1y2=0.
在水资源利用方面,河道能够在一定程度上调配水资源,实现对农业生产所需水资源的供给和满足农村居民生活用水需要。但随着水资源枯竭和污染等问题日益严重,河道的水资源调配功能大幅度降低,河道淤积问题在很多农村较为常见。这些趋势不利于农村发展和农村居民收入水平的提高。因此,农村河道整治工作十分必要。
点评:解析几何法在方程的应用上比较多,在等式的化简方面有些烦琐和技巧性,此解法一定要掌握圆的方程,整个解题过程中,在关键点处的等量代换也十分重要.
二、向量转化法
解法2:建立如图3所示的平面直角坐标系,取AB的中点为H,连接MH,过点M作MK⊥AB.设∠MAB=θ,因为HA=HM,所以∠MHB=2θ.因为AB为直径,所以∠AMB=90°,因为BM⊥BN,所以∠MBN=90°,且所以AM∥BN,所以∠NBC=θ.


三、数量积定义法
所求问题为数量积的格式,可以尝试将所求问题向量先转化,然后运用数量积的定义来解决.
解法3:如图4所示,设∠MAB=θ.因为AB为直径,所以∠AMB=90°.因为BM⊥BN,所以∠MBN=90°,所以AM∥BN,所以∠NBC=θ.
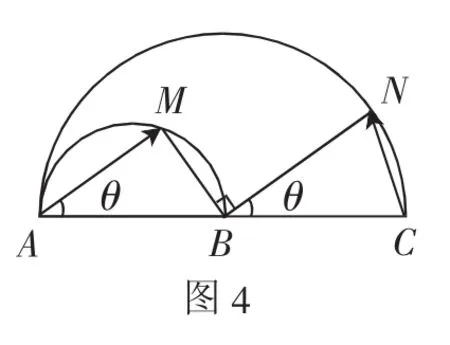

点评:向量数量积的定义是解决数量积问题的最根本的方法,此解法紧紧围绕着数量积的定义展开,当然,将以及∠MAB=θ的设定都非常关键.
四、辅助角法
前面两种解法中,我们都引入了角θ,下面我们仍然借助于辅助角θ,结合数量积的坐标运算形式求解.
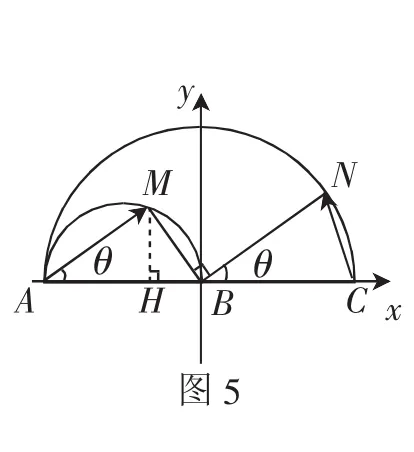
解法4:建立如图5所示的平面直角坐标系,过点M作MH⊥AB,设∠MAB=θ.因为AB为直径,所以∠AMB=90°.因为BM⊥BN,所以∠MBN=90°,所以AM∥BN,所以∠NBC=θ.由题易知,A(-1,0),C(1,0),AM=ABcosθ=cosθ,AH=AMcosθ=cos2θ,MH=AMsinθ=cosθsinθ,所以BH=AB-AH=1-cos2θ=sin2θ,所以M(-sin2θ,cosθsinθ),N(cosθ,sinθ).
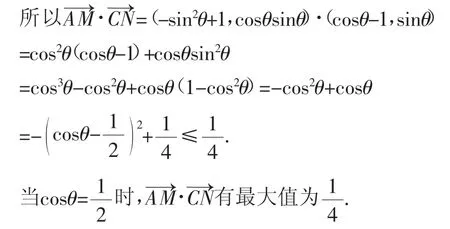
点评:类似于解法2与解法3,也是假设了辅助角θ,用以表示动点M,N的坐标,不同的是,此解法没有涉及向量间的相互转化,而是利用直角三角形中的锐角三角函数,求出动点M,N的坐标,最后化归为关于cosθ的二次函数最大值问题.
五、基本不等式法
基本不等式也是求最值时的常用工具之一,一起来赏析此处的妙用.
解法5:如图6所示,我们可以再以BC为直径作个半圆,线段BN与半圆相交于点M′,连接CM′.因为AB为直径,所以∠AMB=90°.因为BM⊥BN,所以∠MBN=90°,所以AM∥BN.

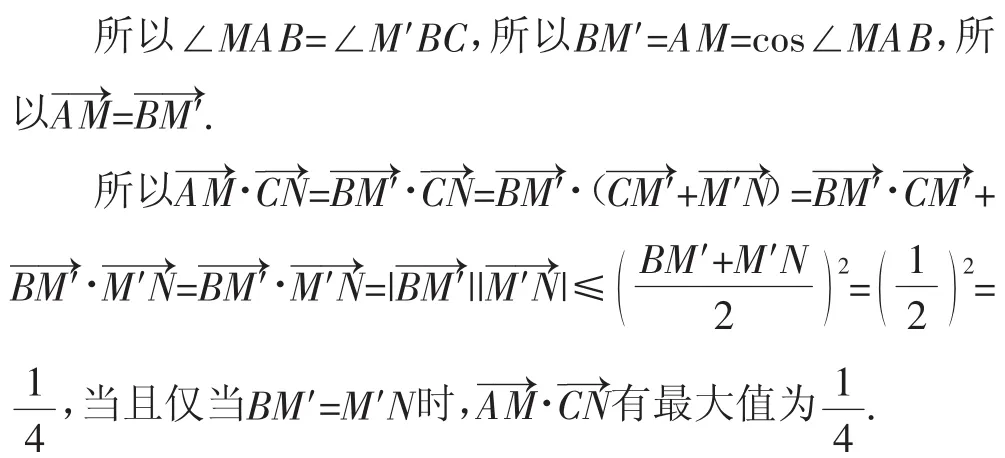
本文主要对一道高三模考试题的解法加以探究,从不同的角度、不同的层面对问题进行剖析,既有常规思路的解法,也有技巧性很强的奇思妙解,希望读者可以回味其中,与您共勉.
