对直线绕点旋转问题的思考—对2017年深圳中考压轴题的剖析、拓展及反思
2018-10-16广东省深圳市龙岗区深圳中学龙岗初级中学518172张家琛
广东省深圳市龙岗区深圳中学龙岗初级中学(518172) 张家琛
本文对2017年深圳中考压轴题第23题最后一问直线旋转45°的问题进行探究与思考,从中体会数学之美.
一、题目呈现
如图1,抛物线经过点A(-1,0),B(4,0),交y轴于点C.
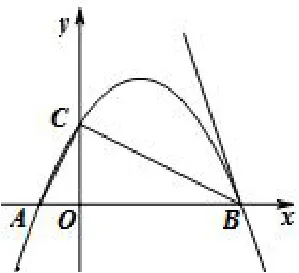
图1
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
二、解析探究及模型构建
1.K型全等模型
K型全等也称半弦图,同时是“一线三等角”相似模型的一种特例.由等腰直角三角形斜放通过作横纵辅助线从而构造的全等.通常思路是“45°⇒等腰直角三角形⇒K型全等”.
如图2,△ABC是等腰直角三角形,作AD,CE垂直过B点的水平线于D、E两点.

图2
结论:△ADB.
证明因为 ∠D= ∠E= ∠ABC=90°,所以∠ABD+∠CBE=∠BCE+∠CBE=90°,所以∠ABD=∠BCE.又因为AB=BC,所以△ADB.
解析一如图3,过点C作CF⊥BC交BE于点F,作FG⊥y轴于点G.因 ∠CBF=45°,所在△BCF是等腰直角三角形.可证 K型全等△FGC△COB,得GF=OC=2,CG=OB=4,即F(2,6).由B(4,0),F(2,6)可得直线BE:y=-3x+12.联立解得x-1=5,x2=4(舍去),故E(5,-3).所以

图3
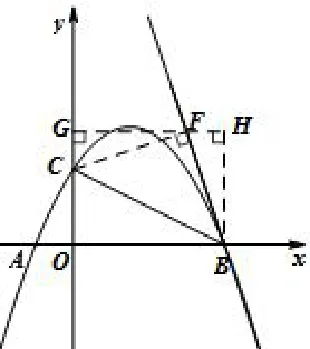
图4
解析二如图4,过点C作CF⊥BE交BE于点F,因∠CBF=45°,则△BCF为等腰直角三角形.构造K型全等△CGF△FHB,则有FG=BH,CG=FH.设FG=BH=x,则CG=FH=x-2.由GH=OB=4可得方程x+(x-2)=4,解得x=3,即F(3,3).可求BF直线解析式,并联立抛物线求出E点坐标,从而求得
解析三如图5,作点C关于直线BE对称于点C′,连接CC′交直线BE于点F,作C′H⊥x轴于点H. 因 ∠CBF=45°,由对称性质可得△CBC′为等腰直角三角形,点K为CC′的中点.构造K型全等△COB△BHC′,则BH=OC=2,OB=C′H=4,即C′(6,4),根据中点坐标公式可求CC′中点F(3,3).可求BF直线解析式,并联立抛物线求出E点坐标,从而求得
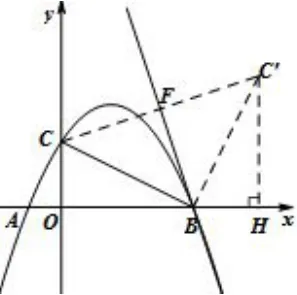
图5
2.角含半角模型
角含半角模型是指满足共端点的等线段和共顶点的倍半角两个特征的图形,可通过旋转使等边重合,拼出全等三角形从而解决问题,常见于以等腰直角三角形或正方形为背景且满足90°含45°的模型.
如图6,在正方形ABCD中,E、F分别是AB、BC边上的点且满足∠EDF=45°.
结论:将△DCF绕点D旋转使得DC与DA重合得△DAG,连接EF,则有△GDE△FDE.
如图7,同理可证:△DCE.

图6

图7
解析四如图8,构造正方形OBMN,直线BE交正方形的边MN于点F.将△COB绕点B顺时针旋转90°于△GMB,则∠CBO= ∠GBM,BC=BG,GM=OC=2,可得G(6,2).连接CF,因∠CBF=45°,由角含半角模型可得△CBF,故CF=GF.设NF=x,则CF=GF=(6-x),NC=2,所以22+x2=(6-x)2,解得即可求BF直线解析式,并联立抛物线求出E点坐标,从而求得
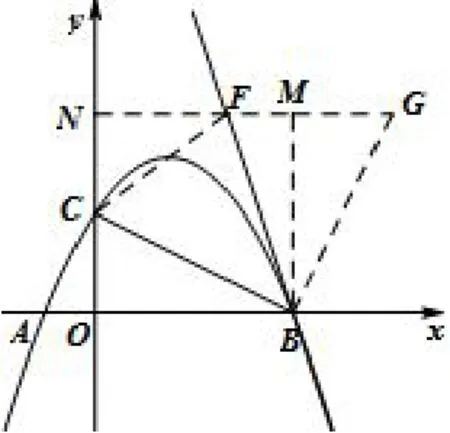
图8
3.“摆正”模型
“摆正”模型是指将斜放的图形(边)通过旋转使得一边平行于坐标轴的图形,根据角的等量代换解决问题.
如图9,∠BAC=α,在y轴上取一点D,使得∠OAD=∠BAC=α.作DE⊥AC于点E,作EF⊥y轴于点F.结论:△AOB~△ADE,△AOD~△DFE.
证明因为∠OAD=∠BAC=α,所以 ∠BAO=∠EAD.因为 ∠BOA=∠EDA=90°,所以△AOB~△ADE.因为∠FDE+∠ODA=∠OAD+∠ODA=90°,所以 ∠FDE= ∠OAD.因为 ∠DOA= ∠EFD=90°,所以△AOD~△DFE.

图9
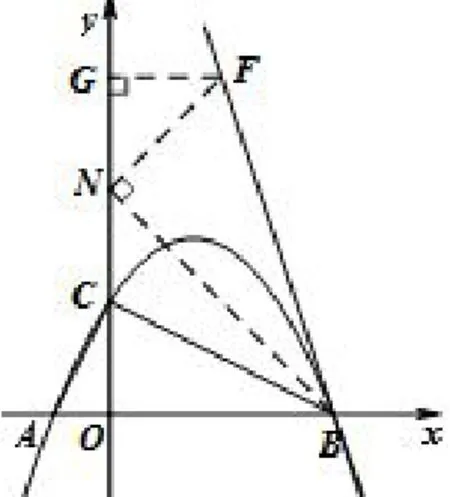
图10
解析五如图10,在y轴上取一点N,使得∠NBO=45°,则△BON为等腰直角三角形.作NF⊥BN交直线BE于F点,再作FG⊥y轴于G点,则△FGN也为等腰直角三角形.因∠NBO= ∠FBC=45°,所以∠CBO= ∠FBN,又因∠COB= ∠FNB=90°,所以△CBO~△FBN.因OB=4,所以由得解得则GN=GF=2,即F(2,6).可求BF直线解析式,并联立抛物线求出E点坐标,从而求得
4.A型相似模型
如图11,∠BAC=α,通过作已知边AB的垂线交x轴和AC分别于D、E两点,作EF⊥x轴于点F.根据A型相似△DOB~△DFE的性质解决问题.
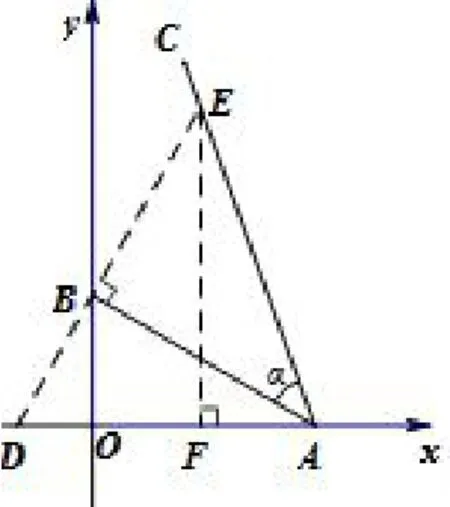
图11
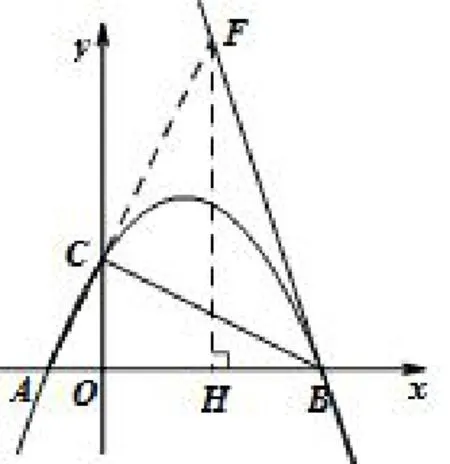
图12
解析六如图12,由A(-1,0),B(4,0),C(0,2),可得AB=5,即△ABC是直角三角形.延长AC交直线BE于点F,作FH⊥x轴于点H.因∠CBF=45°,则△BCF为等腰直角三角形,易证△AOC~△AHF,则即解得OH=2,,即解得FH=6,即F(2,6).可求BF直线解析式,并联立抛物线求出E点坐标,从而求得
三、拓展思考
若旋转角不为45°,上述四种模型还适用吗?很明显,模型1“K型全等型”和模型2“角含半角模型”的前提是特殊角,所以并不适用.下面,我们来看看模型3和模型4是否可以解决旋转角不为45°的问题.
变式1如图13,抛物线y=ax2+bx+2经过点A(-1,0),B(4,0),交y轴于点C.将直线BC绕点B顺时针旋转角度为α,且与抛物线交于另一点E,求BE的解析式.
解析在y轴上取一点N,使得 ∠NBO=α,作NF⊥BN交直线BE于F点,再作FG⊥y轴于G点.可证K型相似△FGN~△NOB,所以有∠FNG=∠NBO=∠FBC=α.因为∠CBO= ∠FBN,∠COB=∠FNB=90°,所以△CBO~△FBG.因OB=4,所以ON=4tanα=3,BN=5.由△CBO~△FBN得得解得由△FGN~△NOB得得解得NG=2,即可求BF直线解析式,并联立抛物线求出E点坐标,从而解决问题.
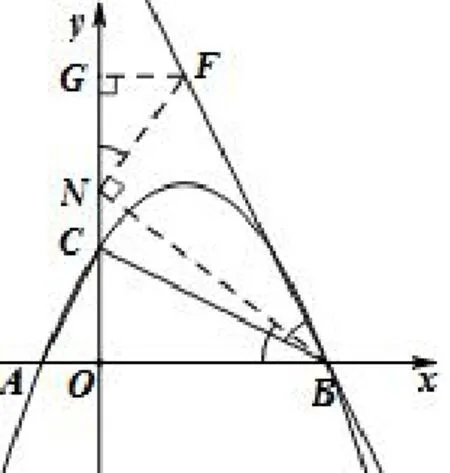
图13

图14
变式2如图14,抛物线y=ax2+bx+2经过点A(-1,0),B(4,0),交y轴于点C.将直线BC绕点B顺时针旋转角度为α,与抛物线交于另一点E,如何求BE的解析式.
解析由A(-1,0),B(4,0),C(0,2),可得AC=即△ABC是直角三角形.延长AC交直线BE于点F,作FH⊥x轴于点H,CF=BC·易证△AOC~△AHF,则即解得OH=2tanα,由即解得FH=2+4tanα,即F(2tanα,2+4tanα).由B、F两点坐标可求直线BE解析式.
四、结语
四种模型体现不同的解析思路,而模型的构建关键在于平时对题型和知识点的归纳和总结.在平时的教学中培养学生的模型构建意识,也是在培养学生的分析问题、归纳总结、解决问题等多种综合性能力.
