圆锥曲线的非对称问题的解题策略
2018-10-16海南省儋州市第一中学571799谢明贤
海南省儋州市第一中学(571799) 谢明贤
在直线与圆锥曲线的位置关系中,常出现这样一类问题:根据题目已知的条件下,得出x1+λx2=0或y1+λy2=0和x1+λx2+µ=0或y1+λy2+µ=0等情形.对于此类问题关键是抓住x1与x2或y1与y2的系数不平衡性(非对称),通过“配方”或点在曲线上调整为对称性.下面本文就这一类问题的解决方法,结合下面的例题,谈一下自己的看法.
例1设椭圆的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为 60°,
(1)求椭圆C的离心率;
解 (1)方法一由已知设F(-c,0),A(x1,y1),B(x2,y2).直线l的方程为:将直线l的方程代入椭圆C的方程,整理得.(b2+3a2)x2+6a2cx+a2(3c2-b2)=0.所以恒成立.由已知

所以,2(x1+x2)2+x1x2+9(x1+x2)+9c2=0,所以
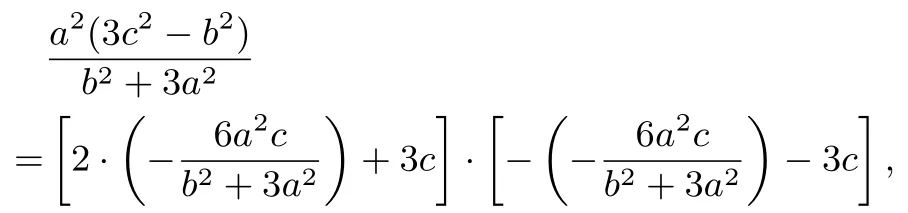
所以,4a6-17a4c2+22a2c4-9c6=0,方程两边同除以a6得,9e6-22e4+17e2-4=0,分解因式得,(9e2-4)(e2-1)2=0.因为0<e<1,所以
方法二由已知设F(-c,0),A(x1,y1),B(x2,y2).直线l的方程为:由已知因为点A,B在椭圆上,所以两式相减得,化简得,结合x1+2x2=-3c.解得,代入直线l的方程为:所以又点A(x1,y1)在椭圆上,则有
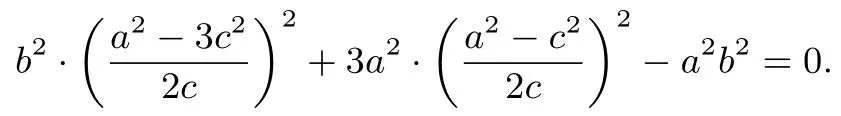
化简得,4a6-17a4c2+22a2c4-9c6=0,方程两边同除以a6得,9e6-22e4+17e2-4=0,分解因式得,(9e2-4)(e2-1)2=0.因为0<e<1,所以
(2)略.

方法二:利用点在曲线上,后作差,把y1与y2的系数不对称化为对称,进而代入曲线方程,解出即可.
例2已知椭圆的离心率长轴的左,右端点分别为A1(-2,0),A2(2,0).
(1)求椭圆的标准方程.
(2)设直线x=my+1与椭圆交于P,Q,直线A1P与A2Q交于点S.试问:当m变化时,点S是否恒在一条直线上?若存在,请求出直线方程.
解(1)椭圆方程为:
(2)方法一:设P(x1,y1),Q(x2,y2),S(x,y).则直线直线联立有,又因为x1=my1+1,x2=my2+1.所以,y1(x+2)-4my1y2+(3x-6)y2=0.

方法二设P(x1,y1),Q(x2,y2),S(x,y).则直线lA1P:直线于是,所以,方程两边平方得,

又因为P,Q在椭圆上,所以,代入(*)则有,

当m=0时,当时,化简得,所以x=4.综上,点S恒在直线x=4上.

方法二:利用点在曲线上,后平方,把x1与x2的系数不对称化为对称,进而利用韦达定理,解出即可.
从以上分析不难看出,圆锥曲线对运算能力的考察是分“层次”的,准确、熟练是基本要求,计算的技能要快速.重点是“合理”,根据具体条件合理确定运算途径,培养学生的思维能力,学会设计合理、简捷的运算途径.在圆锥曲线的解答题中,有些题目并没有直接给出两根之和或两根之积,这样就使得“设而不求”中应用韦达定理造成了一定的困难.若按常规方法,一步一步按题的意思走,计算量偏大.通过以上的实例解答,笔者在这里提供了两种思路,一是通过“配方”的形式,二是充分利用点在曲线上.化不对称为对称,进一步使用韦达定理,减少计算量,从而提高计算速度与准确性.
