基于相位旋转的SCMA码本优化方法

邵 凯, 周博文, 王光宇, 余 贝

(1. 重庆邮电大学移动通信重点实验室, 重庆 400065; 2. 坦佩雷理工大学电子与通信工程系, 芬兰 坦佩雷市 22101; 3. 华为技术有限公司, 广东 深圳 518116)

0 引 言

移动互联网和物联网作为未来移动通信发展的两大主要驱动力[1],正在不断改变着人们的生活方式。移动互联网颠覆了传统通信业务模式,它以各种智能设备(智能手机、平板电脑、可穿戴设备等)作为接入终端,通过技术上的不断创新,使得信息的交互越来越便捷。在移动互联网不断发展的大背景下,虚拟现实、增强现实等新技术的不断突破,给用户带来了前所未有的体验[2]。物联网的应用使得信息的交互不再限定在人与人之间。人与物、物与物之间也将实现互通互联[3],这使得移动通信技术将渗透到更加广阔的领域。车联网、智能家居、移动医疗等将推动千亿设备接入网络。面向2020年及未来,在各种智能设备,移动数据流量的持续爆发式增长下,以及各种应用场景和新业务的不断涌现下,第五代移动通信(the fifth generation mobile communication, 5G)应运而生[4-5]。

每一代移动通信的更新换代都会伴随着多址接入的演进。传统的多址接入方案都可以看作是正交多址接入(orthogonal multiple access, OMA)技术。在OMA中,接入的用户数与正交的资源成正比,很难满足5G海量连接的需求。因此,5G候选多址接入技术主要以非正交多址接入(non-orthogonal multiple access, NOMA)技术为主。稀疏码分多址(sparse code multiple access, SCMA)就是华为公司在2013年提出的一种5G候选新型非正交多址接入方案,旨在有限的频谱资源下接入更多的用户,满足5G海量连接的要求[6]。

SCMA系统发送端,采用码字映射的方式完成传统通信方式中的调制和扩频。SCMA编码的过程实际上就是二进制比特从SCMA码本中挑选码字的过程。一个好的SCMA码本不仅能够提高SCMA系统性能,而且结合先进的具有针对性的译码算法,能够达到降低译码复杂度的目的。SCMA码本设计作为SCMA系统关键技术之一备受业界关注。如何对码本进行优化,使得在不增加系统开销的情况下,尽可能地提高系统性能也是目前研究的热点。

SCMA码本设计过程是一个非凸二次规划二次约束问题,目前并没有求解这一问题的最优方案。通常做法是采用分级优化的思想,将SCMA码本设计分解成优化设计映射矩阵;优化设计母星座;采用星座算子(相位旋转、置换、复共轭等)对母星座进行操作[7],优化码本。文献[8]提出基于Star-QAM的母星座优化方法,在不改变译码复杂度的条件下,降低了比特错误概率(bit error rate, BER)。文献[9]提出使用球形码建立SCMA多维母星座的方法,降低了峰值平均功率比(peak to average power ratio, PAPR)且改善了频谱效率。文献[10]提出将多输入多输出(multiple-input multiple-output, MIMO)系统中的截止频率分析引入码本设计中,通过优化星座旋转角度,改善了系统性能。文献[11]提出了基于星座旋转和交织的方案,以提高频谱效率和功率效率为目的分别进行相应的码本设计。文献[12]提出将网格编码调制技术应用于母星座设计中,结合相位旋转和坐标交织,提出了一种新的标准来选择最合适的置换集合,用于改善每个功能节点的初始信息质量,提高系统性能。文献[13]认为通过修改比特到符号映射,欧式距离可以增加得比传输的数量更快,并提出了一种算法,可有效地找到星座大小为16和32的最优映射。文献[14-15]研究了空间和信号域之间的最优星座分解,提出了一种发送预编码算法,用于直接最小化空间调制的误码率上限,能够联合优化所有接收信号点之间的欧式距离。信号星座图设计是建立以最小误符号率为目标以每个星座符号的幅值和相位为优化变量、以归一化功率为约束的优化求解问题[16]。

综上所示,多数文献对SCMA码本的优化主要集中在母星座设计,而对星座算子仅仅提出了可行性介绍,缺乏相关的理论支撑。基于此,本文主要研究SCMA星座算子,重点研究星座算子中的相位旋转。注意到SCMA与传统多址接入的不同之处在于,相同的时频资源上不再单一的传输一个用户,而是多个用户信号的矢量叠加。本文主要从矢量叠加后的星座图(以下简称合成星座图)的角度出发,通过建立合成星座图上的相位旋转角度的评价标准,达到优化SCMA码本的目的。文章首先介绍上行SCMA系统模型以及SCMA码本设计的步骤,然后重点研究SCMA码本设计过程中的相位旋转角度,并给出相位旋转角度的优化标准,最后通过仿真验证所提方案的可行性及性能。

1 SCMA系统模型

图1是上行SCMA系统模型。此时,用户数J=6;正交时频资源数K=4;每个用户采用的星座点数M=4。SCMA在发送端将输入的比特流直接映射成多维复数域码字,不同用户的码字在相同的正交时频资源上以稀疏扩频的方式非正交叠加,如图2所示。在接收端,则基于码字的稀疏性,采用具有迭代特性的消息传递算法[17-18](message passing algorithm, MPA)进行多用户检测,恢复原始比特流。

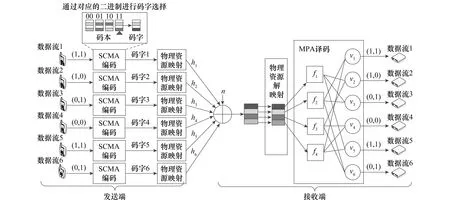
图1 上行SCMA系统模型Fig.1 Uplink SCMA system model

图2 不同用户码字在相同的正交时频资源上的叠加方式Fig.2 Superposition of different user codewords on the same orthogonal time frequency resource

图2中,用户1的码字中非零元素所处的位置为2,4。表示该用户只在正交时频资源2和正交时频资源4上传输信号。为了更加方便地表示这样一种结构,引入稀疏矩阵FK×J,则图1对应的稀疏矩阵为

(1)

式中，FK×J矩阵中的列表示用户,行表示正交时频资源。矩阵中的元素用二进制指示符表示,1表示对应用户在对应正交时频资源上传输信号,0表示不传输信号。

设用户j发送的码字为xj=[x1j,x2j,…,xKj]T,经过信道传输后,接收信号可以表示为

(2)

式中,hj=[h1j,h2j,…,hKj]T表示用户j与基站之间的信道状态信息;diag(hj)是对角阵,第k个对角元素为(hj)k=hkj;n=[n1,n2,…,nK]T表示加性高斯白噪声(additive white gaussian noise, AWGN)。在接收端,则基于最大后验概率准则进行译码,针对X=(x1,x2,…,xJ),则

(3)

2 SCMA码本设计步骤

SCMA编码过程就是通过log2M个比特从K维大小为M的复数码本中挑选码字的过程。SCMA码本设计过程中,在已知J个用户,K个正交时频资源,每个用户实际占用N个正交时频资源,以及每个用户采用M点星座进行传输的前提下,设计码本。保证在接收端有较低的复杂度,同时保证传输信息的有效性和可靠性。

SCMA码本设计过程就是通过星座函数gj产生包含M个N维用户星座Cj。然后通过映射矩阵Vj将Cj映射成SCMA的码本Xj,用户星座的产生过程可以表示为

Cj=gj(bj)

(4)

式中,bj表示用户j输入的比特序列。

由于用户星座Cj与星座函数gj是因变量与映射函数的关系,当自变量一定时,因变量主要由映射函数决定。因此,后文中设计用户星座Cj,实际上就是设计星座函数gj。

SCMA码本用K维向量Xj表示,产生过程可以表示为

Xj=VjCj

(5)

设K维向量V={Vj|j∈[1,J]},K维向量G={gj|j∈[1,J]}。则给定结构为δ(V,G;J,M,N,K)的SCMA码本设计问题可以表示为

V*,G*=arg maxV,Gm(δ(V,G;J,M,N,K))

(6)

式中,m为给定的设计标准。

由于这样一种多维优化问题的适当定义和最优解集目前并没有找到,通常采用一种次优的多级优化方案来解决,主要包括映射矩阵设计、母星座设计以及星座算子3个步骤。

步骤1映射矩阵设计

针对稀疏矩阵FK×J,设

FK×J=(f1,f2,…,fJ)

(7)

式中,fj表示用户j的二进制指示向量。

fj与用户j对应的映射矩阵之间有的关系为

(8)

(9)

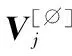
且有下式成立:

max(0,2N-K)≤l≤N-1

(10)

式中,l表示对∀i,j;fi与fj向量相同位置上的元素相等且等于1的个数。

针对l的上边界,考虑到l=N时,两个用户的二进制指示向量相同,在传输过程中两个用户占用相同的正交时频资源,不利于译码。针对l的下边界,考虑到当2N>K时,存在两个用户在实际传输过程中,会占用的相同正交时频资源且最少为2N-K。需要说明的是式(10)是在前面设计要求下两个用户占用相同的时频资源的个数的取值范围,并不是增加的限制条件。

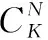
步骤2母星座设计

当映射矩阵设计完成后,设计完成的映射矩阵序列用V+表示,则式(11)可以简化表示为

G+=arg maxGm(δ(V+,G;J,M,N,K))

(11)

此时,码本设计问题转成设计J个不同的N维星座的问题,每个星座包含M个星座点。为了进一步简化优化问题,每个用户的星座点模型通常采用设计母星座,然后对母星座进行各种变换(相位旋转等)得到,称这种母星座进行各种变换的方法为星座算子。则码本设计问题可进一步划分为设计母星座和设计星座算子两个部分分别进行:

Cj=(Δj)C,∀j

(12)

式中,C为母星座;Δj表示星座算子。

母星座C包含了N个维度,每个维度包含M个星座点。为了方便后文表示,用C(n)表示母星座第n个维度的星座。则母星座又可以表示为多个一维母星座向量的组合形式:

C=[C(1),C(2),…,C(N)]T

(13)

每一维度包含M个星座点,各维度母星座表示为

∀n∈[1,N]

(14)

将式(14)代入式(13),则母星座可以表示为

(15)

设计母星座问题也就是设计母星座函数g:

gj=(Δj)g,∀j

(16)

母星座设计方案有多种,其中母星座交织方案由于设计简单,性能优良(相比不进行交织的方案,可以显著增加码字之间的欧式距离)，得到了较为广泛的应用。母星座交织方案的主要思想是首先设计星座点在一条直线上的母星座,对于第n维度的母星座,当n为奇数时,所得母星座与第一维度母星座相等,当n为偶数时,所设计的母星座对第一维度母星座进行交织。需要说明的是,母星座并非一定要在一条直线上,在一条直线上的母星座,旋转简单、母星座只有在旋转180°后才会恢复原状,因此合成星座图的星座点能够最大程度的分散,不会像QAM等星座图,在旋转90°后便恢复原状。

称直线上离原点最近的星座点为基准星座点,则母星座第一维度主要通过基准星座点乘以星座点增益得到,母星座第一维度定义为

(17)

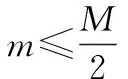
即

C(1)=[-αM/2-1s,…,-αM/4s,-αM/4-1s,…,-s,

s,…,αM/4-1s,-αM/4s,…,-αM/2-1s]

(18)

式中,α表示各星座点与基准星座点的比值所对应幂的底数；s表示基准星座点到原点的欧氏距离。需要说明的是,式(18)对一个正交时频资源上传输单个用户来说一维星座设计效率会远低于二维星座,但是对多个用户,最后译码性能的好坏取决于一个正交时频资源上多个用户信号叠加之后的合成星座图的好坏,因此对母星座的维度并不敏感。

对于奇数维度,则有

C(n)=C(1),n为奇数

(19)

对于偶数维度,若M=2,则只需要将第一维度码字逆序即可,若M≥2,则M必定可以被4整除(M∈{2,4,8,16,32,64…})。此时,可以将式(18)分为4个部分:

(20)

奇数维度交织可以表示为

C(n)=(q1,q2,q3,q4),n为奇数

(21)

考虑用户码字的对称性,偶数维度可以表示为

C(n)=(-q3,q4,q1,-q3),n为偶数

(22)

每个用户对应的符号平均能量为

(23)

式中,En表示用户在第n维母星座的平均能量。

步骤3星座算子

当母星座设计完成以后,则原始的SCMA码本优化问题进一步简化为优化用户,使得在同一正交时频资源上传输的用户之间能够尽量地减少干扰,更容易区分。进一步简化的优化问题可以表示为

(24)

星座算子可以包含以下几个方面:

(1) 相位旋转

z=eiφz0

(25)

(2) 缩放

缩放操作用⊗:r表示:

z=rz0

(26)

(3)复共轭变换

(27)

综合以上3种操作,用户j的星座算子Δj可以定义为

(28)

即星座算子表示对原始信号进行相位旋转、缩放、复共轭的映射。

3 SCMA相位旋转角度分析

3.1 相位旋转角度的影响

这里以图1为例说明,其中J=6,K=4,N=2,M=4,df=3。稀疏矩阵如式(1)所示。用户在不同的正交时频资源上的母星座不同,但在正交时频资源上,不同用户采用的母星座可以相同。如式(29)所示就是其中一种用户在正交时频资源上的母星座的对应关系,为了后文描述的方便,称其为星座矩阵。星座矩阵的列对应用户,行对应正交时频资源。从星座矩阵中可以看到,用户1在正交时频资源2和资源4上分别采用了母星座C(1)和C(2),正交时频资源1上,用户2和用户3采用了相同的母星座C(1)。

(29)

以正交时频资源1为例,来研究不同的相位旋转角度的影响。正交时频资源1上同时传输3个用户:用户2、用户3和用户5。用户2和用户3采用母星座第1维度C(1),用户5采用母星座第2维度C(2)。用户j在正交时频资源k上基于母星座的相位旋转角度用θkj表示,则正交时频资源1上,用户相位旋转角度分别表示为θ12,θ13,θ15。用户星座经过相位旋转后,星座矩阵可以进一步表示为

(30)

设用户j在正交时频资源k上采用的星座点为Ck-j(wkj),wkl∈{0,1,…,M-1}或用二进制表示,例如M=4,则wkj∈{0,1,…,M},则有

Ck-j(wkj)=ckwkj·ejθkj,wkj∈{0,1,…,M-1}

(31)

例如用户2在正交时频资源1上的星座点共M=4个,分别为

C1-2(0)=c10·ejθ12,C1-2(1)=c11·ejθ12,

C1-2(2)=c12·ejθ12,C1-2(3)=c13·ejθ12。

图3为正交时频资源1上,用户不同旋转角度(θ12=0°,θ13=144°,θ15=88.6°)下的星座图。

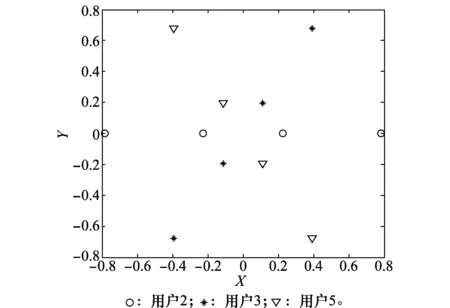
图3 用户星座图Fig.3 User constellation

在接收端接收到的是多个用户在相同的时频资源上叠加的信号,用户2、用户3、用户5分别经过不同的旋转角度后得到的合成星座图分别如图4(a)和图4(b)所示。

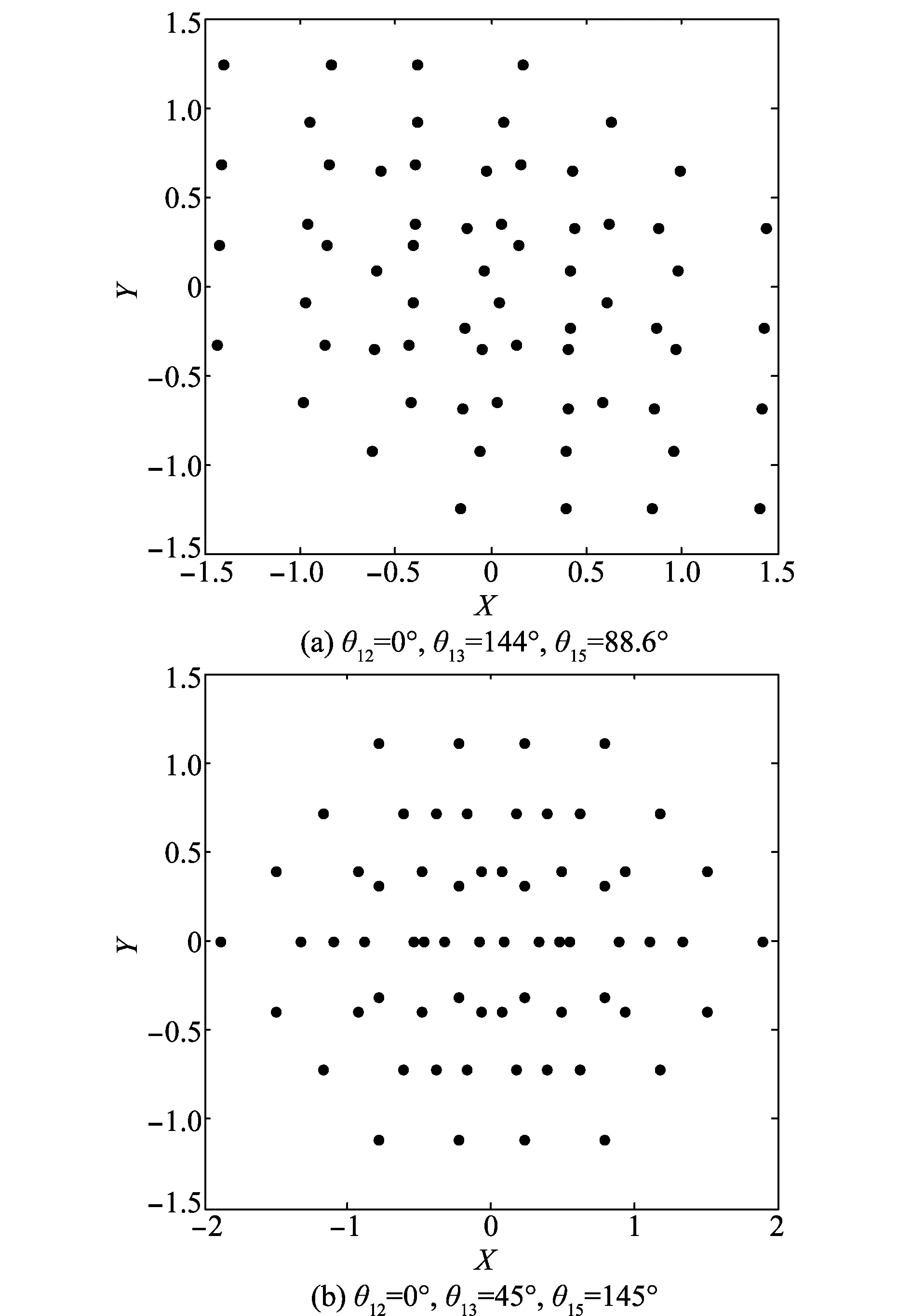
图4 不同旋转角度下的合成星座图Fig.4 Synthesis constellation of different rotation angles

从图4中可以看到,不同用户的旋转角度会对接收信号合成星座图产生影响,从而影响最后的译码效率及译码准确度。因此,可以从最终合成星座图出发,找到一种评价标准,优化相位旋转角度。需要说明的是,本文是以高斯信道下的相位旋转进行说明,如果是瑞利信道或其他信道,要将信道复增益与星座图相乘后再叠加。

3.2 两种相位旋转角度的评价标准

(1)评价标准1:最大化最小欧氏距离

本方案首先求出在不同旋转角度下,星座图中星座点的最小欧氏距离,然后找到不同旋转角度下求出的最小欧氏距离最大的相位旋转角度,即为本方案的最优旋转角度。为了简化表示,称这种方案为基于最大化最小欧氏距离的旋转标准(rotation based on maximizing minimum euclidean distance, M-rotation)方案,优化方案如下:

目标函数为

max{Mθkξk}

(32)

约束关系为

Mθkξk=min{dk,pq|p∈[1,Mdf],q∈[1,Mdf],p≠q}

(33)

dk,pq=|Sk,p-Sk,q|

(34)

(35)

Ck-l(wkl)=ckwkl·ejθkl

(36)

θkl∈[0°,180°]

(37)

k∈[1,K]

(38)

其中,式(32)对M取极大值,式(34)对d取极小值。ξk表示在正交时频资源k上传输的用户集合,Mθkξk表示θkl(l∈ξk)时,合成星座图星座点间的最小欧氏距离;p、q表示合成星座图上的星座点编号;dk,pq表示合成星座图上编号为p和q的两个星座点之间的欧氏距离;Sk,p表示正交时频资源k上的合成星座图上编号为p的星座点的坐标。

由于相位旋转角度的相对性,在正交时频资源1上,可以固定用户2的相位旋转角度(θ12=0°),旋转用户3和用户5得到最优旋转角度。为了更好地进行比较,对最大化最小欧式距离进行归一化处理,得到归一化最大化最小欧式距离为

(39)

不同相位旋转角度下的归一化最大化最小欧氏距离等高线如图5所示。

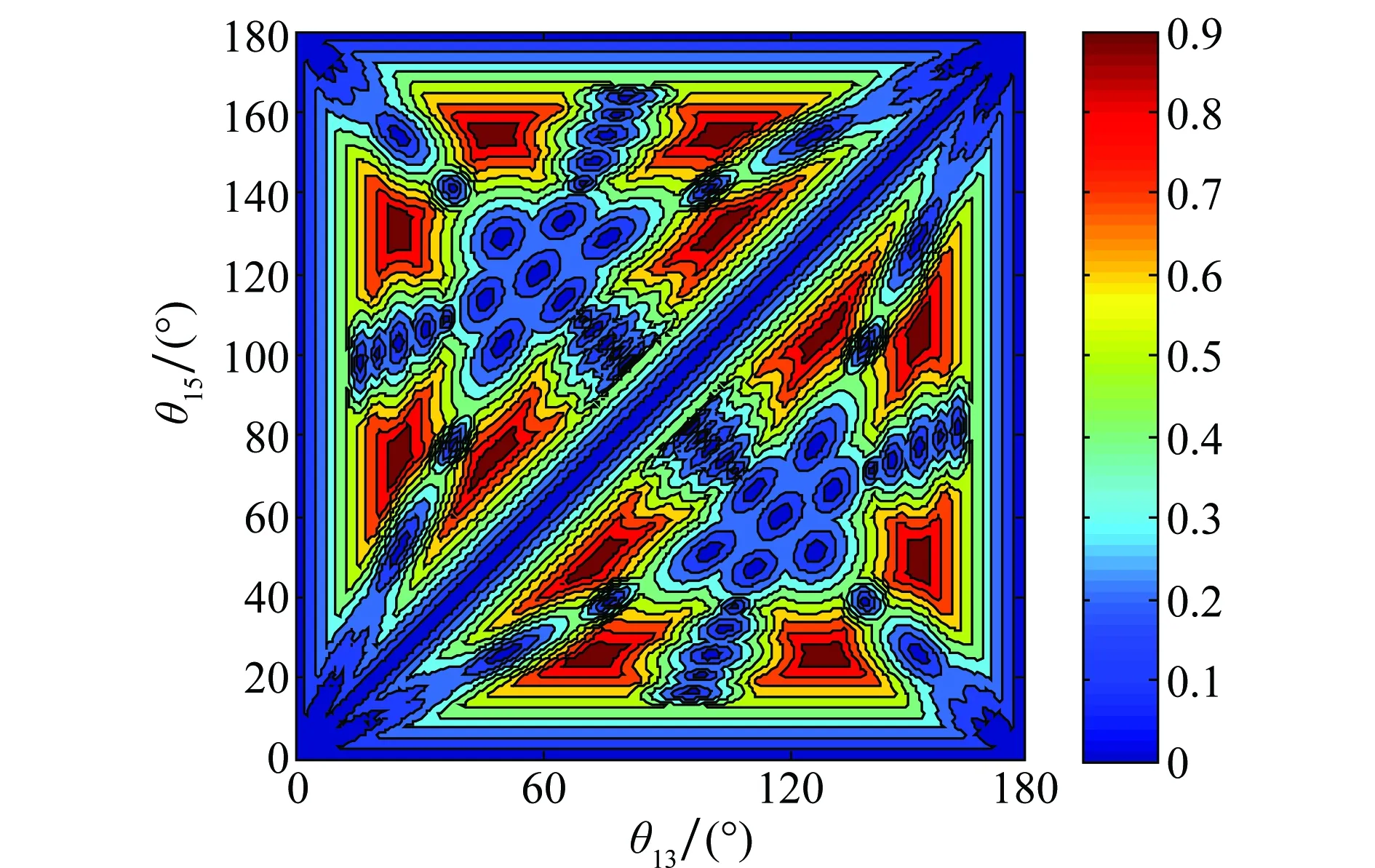
图5 不同相位旋转角度下的归一化最大化最小欧氏距离等高线Fig.5 Normalized maximization of minimum Euclidean distance contour under different phase rotation angles

图5中红色区域表示不同相位旋转之后归一化最大化最小欧氏距离最大的区域,蓝色区域表示欧氏距离最小的区域。从图中大致上可以看到,有12个区域存在评价标准1下的最优旋转角度。通过对优化问题精确求解,可以得到评价标准1下的最优旋转角度分别为

①θ12=0°,θ13=27°,θ15=74°；

②θ12=0°,θ13=74°,θ15=27°；

③θ12=0°,θ13=134°,θ15=27°；

④θ12=0°,θ13=27°,θ15=134°；

⑤θ12=0°,θ13=74°,θ15=48°；

⑥θ12=0°,θ13=134°,θ15=108°；

⑦θ12=0°,θ13=48°,θ15=74°；

⑧θ12=0°,θ13=108°,θ15=134°；

⑨θ12=0°,θ13=155°,θ15=48°；

⑩θ12=0°,θ13=48°,θ15=155°；

(2)评价标准2:指数平均

本方案首先求出在不同旋转角度下,合成星座图上各星座点相互欧氏距离的指数平均值,然后找到不同旋转角度下求出的指数平均值最小的相位旋转角度,得出本方案的最优旋转角度。为了简化表示,称这种方案为基于指数平均的旋转(rotation based on exponential average, E-rotation)方案,优化方案如下:

目标函数为

min{Eθkξk}

(40)

约束关系为

(41)

dk,pq=|Sk,p-Sk,q|

(42)

(43)

Ck-l(wkl)=ckwkl·ejθkl

(44)

θkl∈[0°,180°]

(45)

k∈[1,K]

(46)

式中,ξk表示正交时频资源k上的用户集合;Eθkξk表示合成星座图星座点之间欧氏距离的指数平均,p、q表示合成星座图上的星座点编号;dk,pq表示合成星座图上编号为p和q的两个星座点之间的欧氏距离;Sk,p表示合成星座图上编号为p的星座点的坐标。

同样设θ12=0°,旋转用户3和用户5的相位角度。对指数平均做归一化处理,得到归一化指数平均为

(47)

不同相位旋转角度下的归一化指数平均等高线如图6所示。需要注意的是,虽然目标函数是求最小值,但归一化过程中,如式(47),ηE与Eθkξk成反比,因此最优值存在图6中红色区域位置。通过对优化问题的精确求解,可以得到评价标准2下的最优旋转角度分别为

①θ12=0°,θ13=60°,θ15=120°；

②θ12=0°,θ13=120°,θ15=60°。

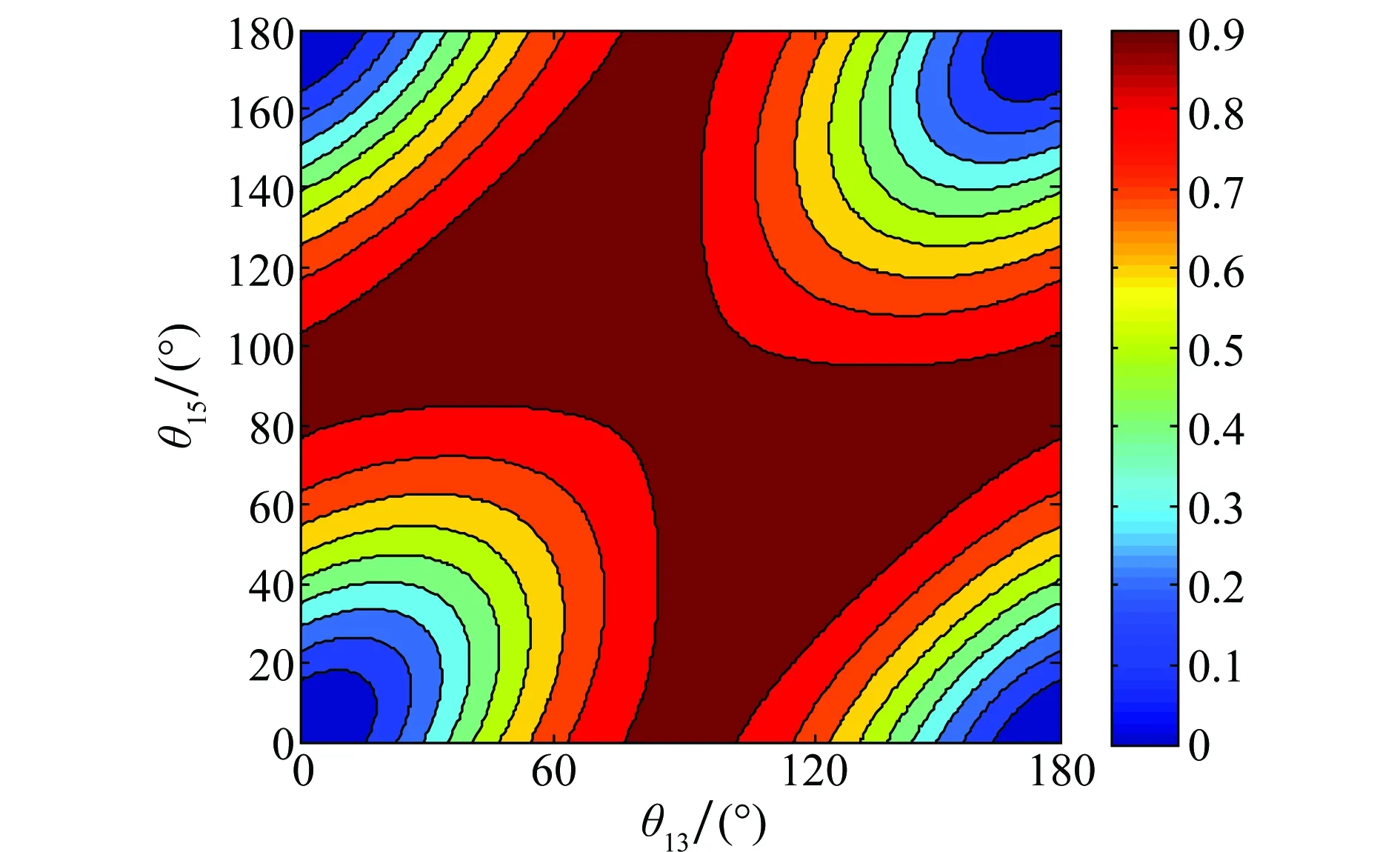
图6 不同相位旋转角度下的归一化指数平均值等高线Fig.6 Normalized exponential average contour of different phase rotation angles

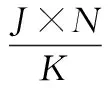
4 仿真分析

4.1 BER对比

M-rotation方案所求旋转角度较多,这里首先针对M-rotation方案中求得的不同旋转角度进行仿真验证,考虑到对称性,主要选取在图5中不对称的3种旋转角度,分别为:θkl∈{0°,48°,155°}、θkl∈{0°,28°,74°}、θkl∈{0°,108°,134°}。得到的仿真结果如图7所示。

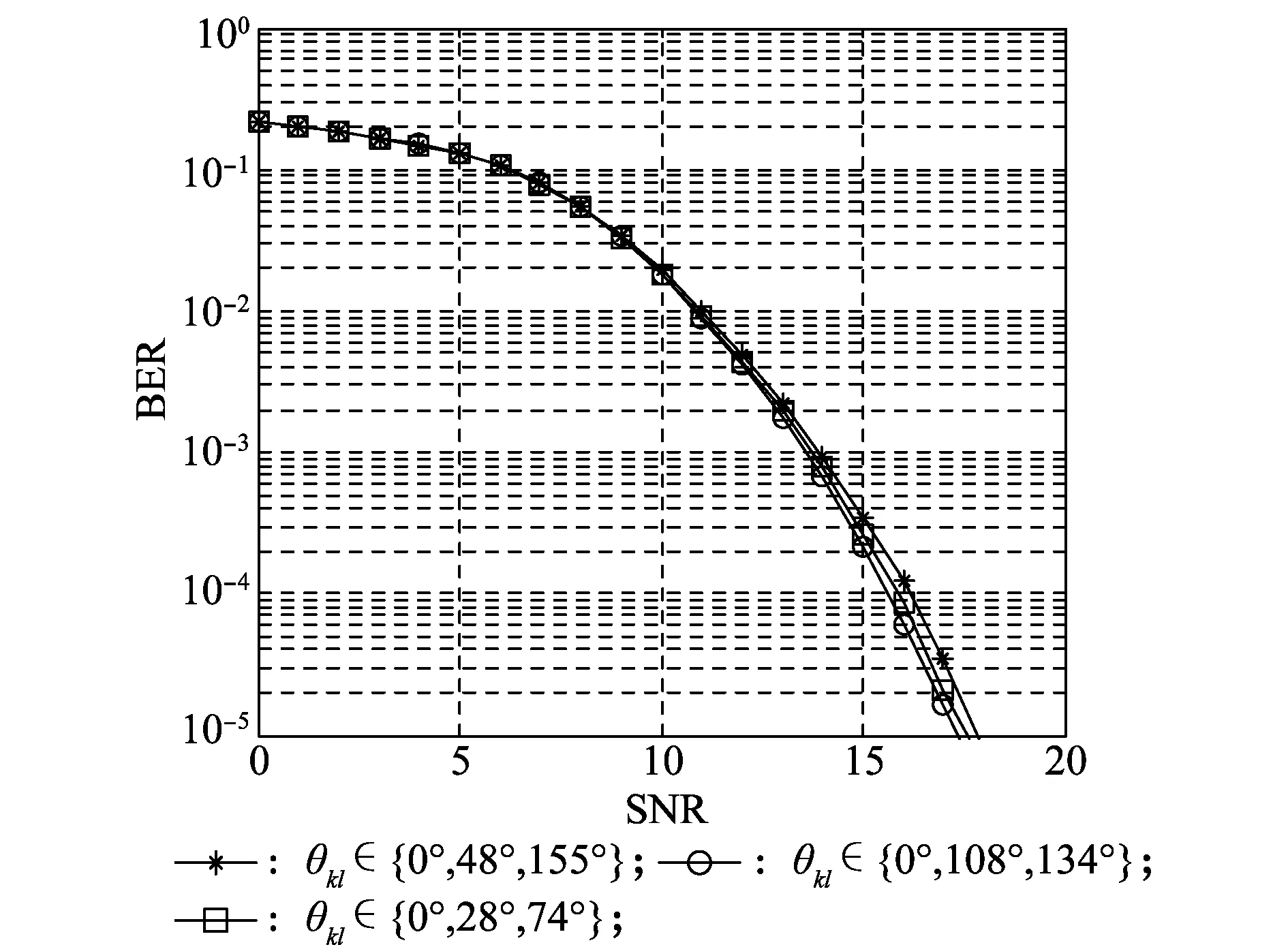
图7 M-rotation方案不同旋转角度的BER对比Fig.7 BER comparison of different rotation angles under M-rotation scheme

从图7中可以看到,3种角度下得到的仿真曲线整体上相差不大。在高信噪比条件下存在一些细微差别,其中旋转角度θkl∈{0°,108°,134°}略优于旋转角度θkl∈{0°,28°,74°},且均略优于θkl∈{0°,48°,155°}。

为了验证所提两种方案的系统性能,分别对采用E-rotation方案产生的码本、M-rotation方案产生的码本、无相位旋转(no phase rotation, N-rotation)方案(相位旋转角度为0°)产生的码本以及华为公司提供的码本(简称HW-rotation码本)进行仿真,比较各种方案的BER性能。具体仿真参数如表 1所示。

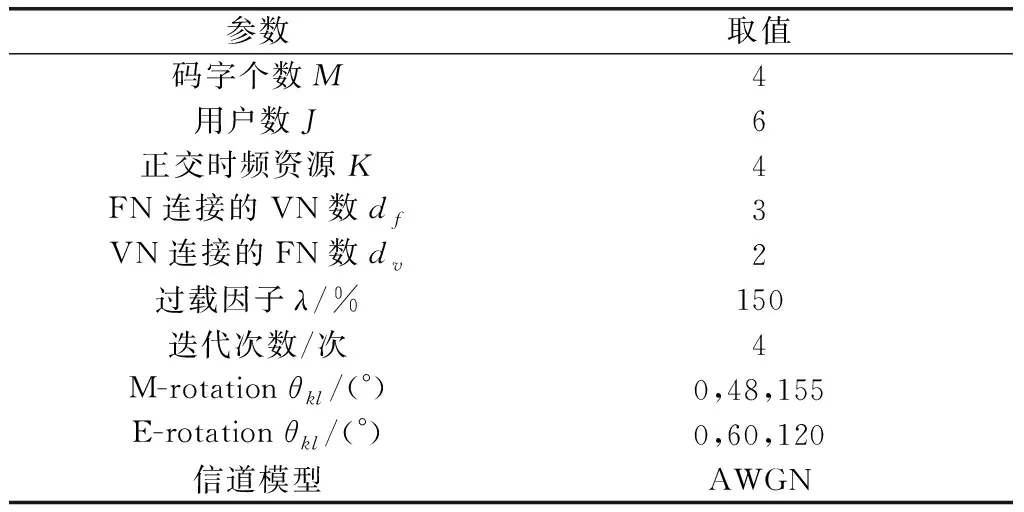
表1 不同码本误比特率对比仿真参数表

得到的不同评价标准下的BER对比如图8所示。

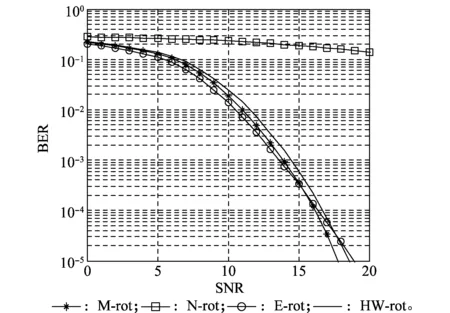
图8 不同评价标准下的BER对比Fig.8 BER comparision under different evaluation criteria

从图8中可以看到,两种评价标准均能得到比较理想的结果,采用E-rotation方案整体上略优于采用M-rotation方案,且两种方案整体上均优于HW-rotation码本。但是在高SNR条件下,采用E-rotation方案优势会逐渐减少,M-rotation方案优于E-rotation方案。从图8中同时可以看到,经过优化的方案,性能均远远优于不进行任何旋转优化的N-rotation方案。因此,优化相位旋转角度对提升系统性能具有重要意义。

需要说明的是,其他SCMA码本优化方案主要基于母星座进行优化设计,而本文所提方案是基于星座算子中的相位旋转进行优化,因此,可以将本文所提优化方案与前文所述的基于母星座的优化设计结合,达到更大程度上性能的提高。也由于此原因,本文所提方案无法直接与基于母星座进行优化设计的方案对比,所以本文主要对比了同样进行了相位角度优化的HW-rotation码本。由于3种方案对系统性能的影响相差不大,为了能够说明相位旋转角度优化的重要性,引入了不经过任何旋转角度处理的N-Rotation方案码本进行对比。

4.2 译码复杂度对比

为了验证所提方案对译码复杂度的影响,分别采用E-rotation方案产生的码本、M-rotation方案产生的码本、不经过相位旋转的N-rotation方案产生的码本以及HW-rotation码本进行仿真比较。其中,译码算法主要采用MPA和部分外部信息传递的消息传递算法[19](partial extrinsic information transmission of MPA, PEIT-MPA)。仿真参数见表2。

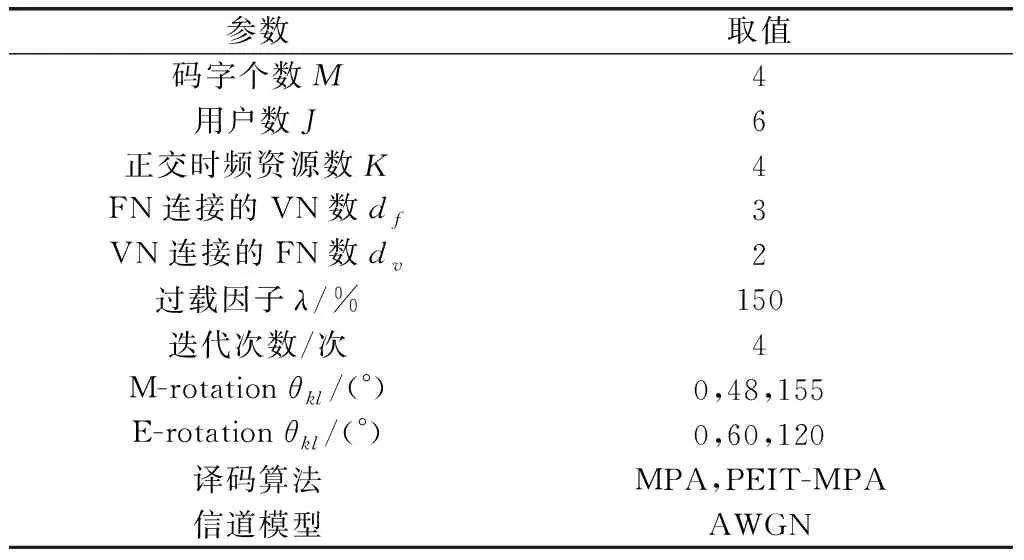
表2 不同码本译码复杂度对比仿真参数表

PEIT-MPA门限值主要选取ft=0.001、ft=0.01、ft=0.1三组值,原始MPA可以看作是PEIT-MPA的特例,即ft=0。得到的4组仿真结果分别如图9～图12所示。

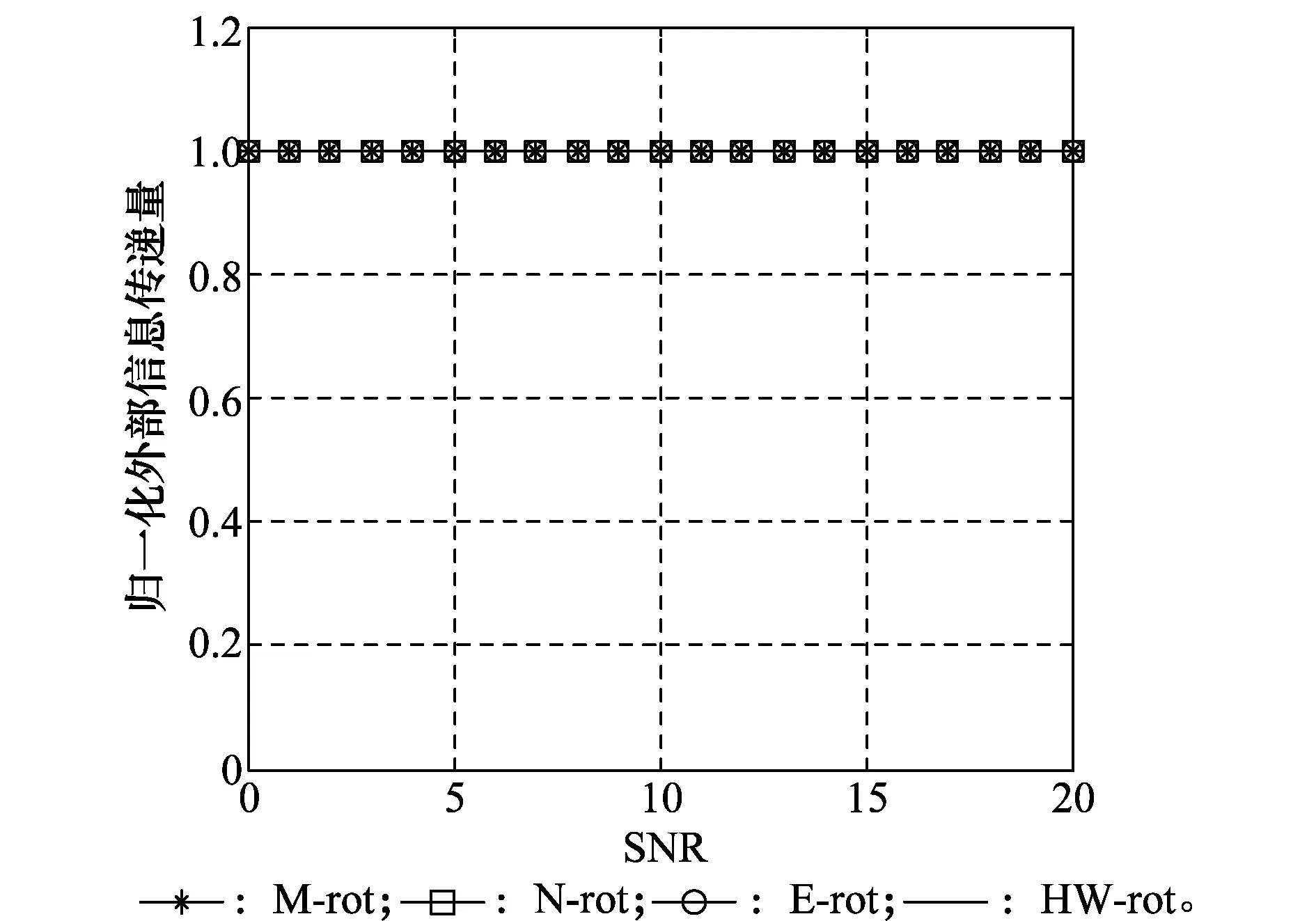
图9 采用MPA时不同码本的归一化外部信息传递量对比Fig.9 Compared the normalized external information transfer of different codebook by using MPA

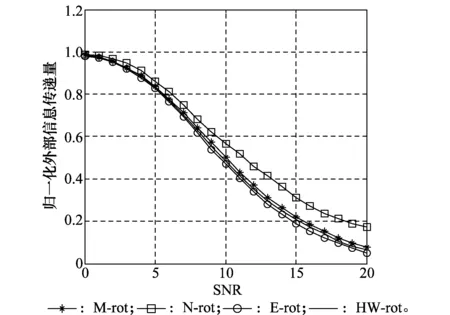
图10 采用PEIT-MPA(ft=0.001)时不同码本的归一化外部信息传递量对比 Fig.10 Compared the normalized external information transmission of PEIT-MPA(ft=0.001)

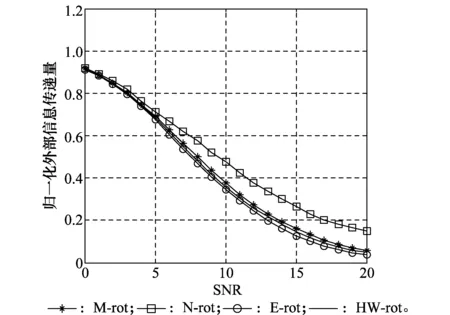
图11 采用PEIT-MPA(ft=0.01)时不同码本的归一化外部信息传递量对比 Fig.11 Compared the normalized external information transmission of PEIT-MPA (ft=0.01)

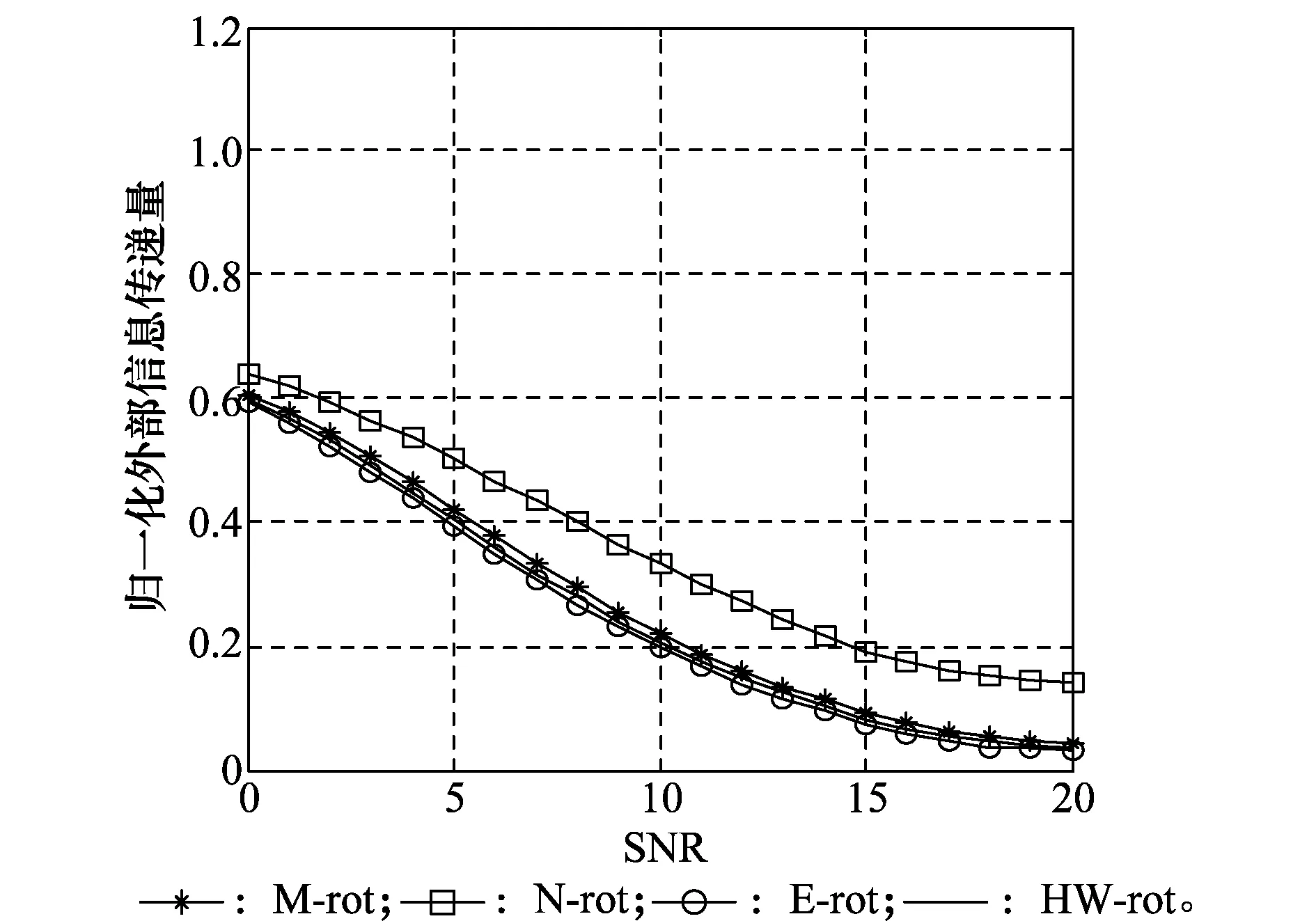
图12 采用PEIT-MPA(ft=0.1)时不同码本的归一化外部信息传递量对比 Fig.12 Compared the normalized external information transmission of PEIT-MPA (ft=0.1)

从图9中可以看到,不同方案得到的码本在采用MPA时,译码复杂度并没有区别,而从图10～图12中可以看到,不同方案得到的码本对PEIT-MPA的译码复杂度会有一定的影响。采用E-rotation方案时更有助于PEIT-MPA复杂度的降低,其次是HW-rotation码本和M-rotation方案码本。复杂度不同的主要原因是各种方案下,导致合成星座图不一样,从而影响了译码过程中接收信号的概率密度函数值,导致译码复杂度不同。

5 结束语

本文主要针对SCMA在高过载条件下,用户共用相同的正交时频资源时由于码字之间的相互碰撞而导致的性能下降问题,研究了星座算子中相位旋转对系统性能的影响,从合成星座图的角度出发,提出两种评价标准用户优化相位旋转角度:M-rotation方案和E-rotation方案,从而达到优化SCMA码本的作用。仿真结果表明,所提的两种方案均能较好的评价用户的相位旋转角度的优劣。